数控机床综合误差分析与建模研究*

李志荣 封志明②

（①西华大学机械工程与自动化学院，四川成都610039;②四川大学制造科学与工程学院，四川成都 610065）

数控机床的加工精度是数控机床性能的主要标志之一。从运动学角度来讲，机床的加工精度最终是由机床上刀具与工件间的相对位移决定的，刀具与工件间的综合误差（位置及方向误差）会影响刀具与工件间的相对位移。要提高机床的加工精度必须对机床的误差进行补偿［1］。误差补偿技术的实施可分为3个步骤［2］:误差测量、误差建模及误差补偿，而误差补偿系统的性能主要依赖于所建立的误差模型，因此误差模型成为误差补偿系统的关键因素。国内外研究人员在机床误差建模方面做了大量研究［3－4］，主要有三角几何法、误差矩阵法、神经网络法、矢量描述法、刚体运动学法和多体系统理论法等。其中多体系统理论对复杂机械系统有较强的概括能力和特有的系统描述方式，可全面考虑影响系统的各项因素及相互耦合关系，因而其广泛应用于复杂机械系统运动误差建模［5－6］。如文献［7］基于多体系统理论，建立了加工中心热误差模型，并提出其误差补偿方法，实践结果表示利用所建立的热误差模型进行误差补偿的效果显著。文献［8］采用改进的多体系统建模理论对激光拼焊生产线运动误差进行研究，结果表明所建立的模型能有效预测激光拼焊线的运动误差。

本文通过分析机床误差来源及各运动副的误差运动学原理，利用齐次坐标变换方法对一台三轴数控机床进行综合误差建模。

1 机床误差源分析

在机床加工过程中，各种误差源作用在工件的成形过程中，使加工进程偏离给定进程，造成成品加工误差。误差按其来源来分可分为内部误差和外部误差两种。其中内部误差源主要包括加工原理误差、几何误差、热误差、切削力误差、摩擦力、振动等。大量研究统计（如表1所示）表明几何误差和热误差占总误差的主要部分，对这两项误差的补偿研究已经取得了成效，而切削力误差对机床精度的影响作用也日益显著［8］。因此本文将几何误差、热误差和切削力误差综合考虑来建立机床的综合误差模型。

表1 机床各误差源比例分配［6］

2 机床误差元素分析

2.1 几何误差

对于一台三轴数控机床来说，其运动坐标包括X、Y、Z三个移动坐标轴。在理想情况下，与机床每个运动副相关的自由度应该只有一个:其中移动副为一个平移自由度，转动副为一个旋转自由度，但是在机床实际运行过程中，由于机床制造和装配上的误差，每个运动副往往存在6个自由度，即3个平移误差，3个转动误差。以X轴为例，沿X轴平动的6项运动误差如图1所示。

因此，3个移动副共有18项几何误差，加上3个轴与轴之间的3项垂直度误差及主轴误差，共26项几何误差。其中X轴移动时有线性误差 εxx、εyx、εzx三项，转角误差 δxx、δyx、δzx三项;Y轴移动时有线性误差εxy、εyy、εzy三项，转角误差 δxy、δyy、δzy三项;Z轴移动时有线性误差 εxz、εyz、εzz三项，转角误差 δxz、δyz、δzz三项;主轴共5项运动误差:3个方向的移动误差εxs、εys、εzs，2 个转角误差 δxs（θ）、δys（θ）。

2.2 热误差

机床热变形是导致热误差的直接原因，机床各部分在内部热源（如电动机、轴承摩擦、导轨摩擦等）和外部热源（如室温、辐射、对流等）的作用下，产生热量并传给机床各部位产生温差并使各零部件产生热变形。对于三轴数控机床来说，各运动轴及主轴的热误差共14项，分别为:X轴原点在3个方向的热漂移误差εxx（t）、εyx（t）、εzx（t）;Y轴原点在3个方向的热漂移误差εxy（t）、εyy（t）、εzy（t）;Z轴原点在3个方向的热漂移误差εxz（t）、εyz（t）、εzz（t）;主轴原点在3个方向的热漂移误差 εxs（t）、εys（t）、εzs（t），2 个方向的转角误差 δxs（t）、δys（t）。

2.3 切削力误差

切削力误差是指数控机床加工时产生的切削力导致刀具、工件、机床部件等变形，从而使实际切削位置与理论切削位置发生偏移而产生的误差［8］。对于三轴数控机床来说，各运动轴及主轴的切削力误差共23项分别为:X轴在三个坐标轴方向的切削力误差εxx（f）、εyx（f）、εzx（f），转角误差 δxx（f）、δyx（f）、δzx（f）;Y轴在3个坐标轴方向的切削力误差 εxy（f）、εyy（f）、εzy（f），转角误差 δxy（f）、δyy（f）、δzy（f）;Z轴在3 个坐标轴方向的切削力误差 εxz（f）、εyz（f）、εzz（f），转角误差 δxz（f）、δyz（f）、δzz（f）;主轴共 5 项切削力误差:3 个方向的移动误差 εxs（f）、εys（f）、εzs（f），2 个转角误差 δxs（f）、δys（f）。

3 误差建模

基于多体系统理论的误差建模方法是用拓扑结构将研究对象进行抽象，用低序体阵列描述拓扑结构中各体之间的关联性。

3.1 拓扑结构及低序体阵列

描述多体系统拓扑结构的方法有两种，一种是基于图论的描述方法，另一种是运用低序体阵列进行描述。用低序体阵列描述多体系统拓扑结构显得更简洁方便，它是一种适用于计算机自动描述多体系统的方法。因此本文选择用低序体阵列对三轴数控机床的拓扑结构进行描述。三轴数控机床的结构示意图如图2所示，拓扑结构如图3所示，低序体阵列如表2所示，自由度码如表3所示。

表2 三轴机床的低序体阵列

表3 三轴机床的自由度

3.2 运动特征矩阵

（1）相邻体0和相邻体1之间运动特征矩阵

相邻体0和1之间的理想静止、理想运动特征矩阵为

体间实际静止、运动误差特征矩阵为

（2）相邻体1和相邻体2之间运动特征矩阵

相邻体1和2之间的理想静止、理想运动特征矩阵为

体间实际静止、运动误差特征矩阵为

（3）相邻体0和相邻体3之间运动特征矩阵

相邻体0和3之间的理想静止、理想运动特征矩阵为

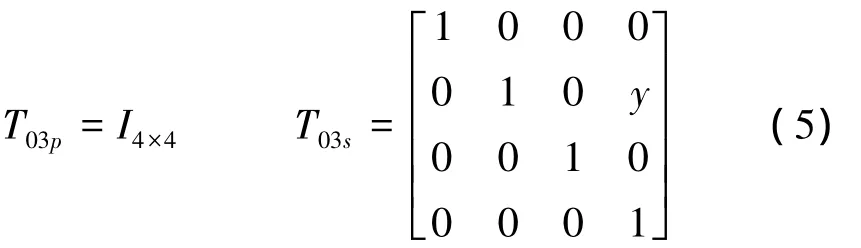
体间实际静止、运动误差特征矩阵为

（4）相邻体3和相邻体4之间运动特征矩阵

相邻体3和4之间的理想静止、理想运动特征矩阵为

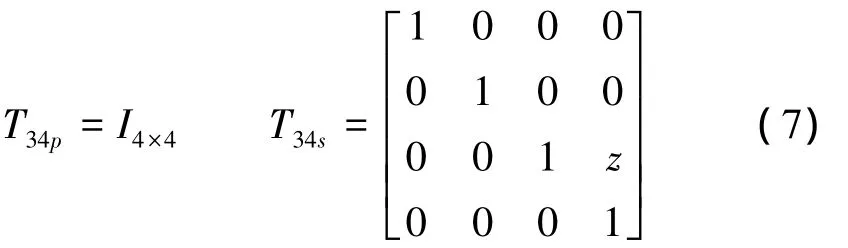
体间实际静止、运动误差特征矩阵为

（5）相邻体4和相邻体5之间运动特征矩阵

相邻体4和5之间的理想静止、理想运动特征矩阵为

体间实际静止、运动误差特征矩阵为

（6）相邻体5和相邻体6之间运动特征矩阵

相邻体5和6之间的理想静止、理想运动特征矩阵为

体间实际静止、运动误差特征矩阵为

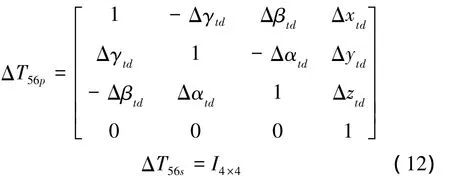
3.3 综合误差建模

（1）理想成形函数

设刀具成形点在刀具坐标系统内的坐标为

刀具成形点在工件坐标系统内的理想成形函数为

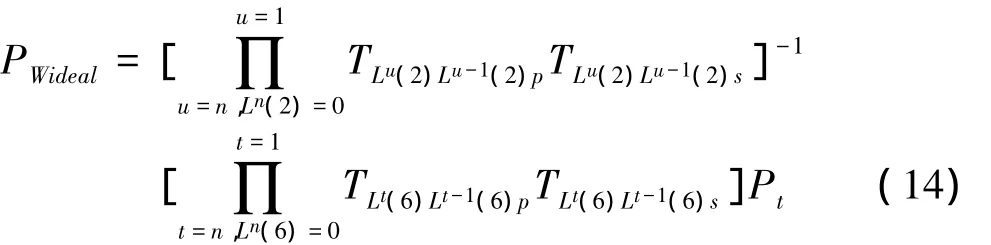
（2）实际成形函数

刀具成形点在工件坐标系统内的实际成形函数为

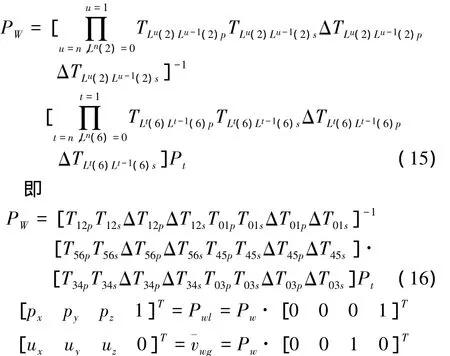
（3）空间误差模型

在实际成形运动中，刀具成形点的实际位置不可避免地会偏离理想位置，产生空间位置误差EP和刀具状态偏差刀具成形点的综合空间误差即为

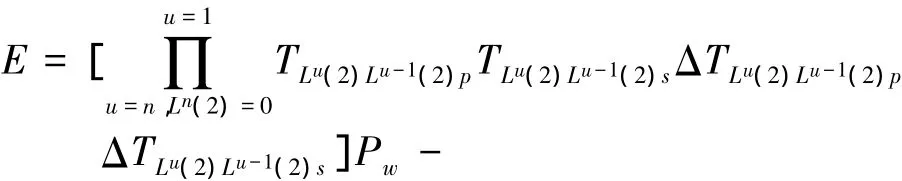
刀具成形点的空间位置误差为

刀具姿态误差为

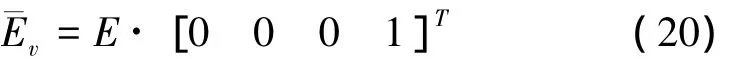
4 结语

本文根据机床结构特征及多体系统理论分析的特点，利用特征矩阵表示多体系统中间体的相对位置和姿态，给出了机床综合误差的建模过程，并得到了包含几何误差、热误差、切削力误差在内的综合误差数学模型。该建模方法为其他类型机床的误差建模提供参考，并为进一步的机床误差辨识及数控补偿打下了基础。

［1］杨建国.数控机床误差综合补偿技术及应用［D］.上海:上海交通大学，1998.

［2］Hsu Y Y，Wang S S.A new compensation method for geometry errors of five－axis machine tools［J］.International Journal of Machine Tools ＆Manufacture，2007，47:352－360.

［3］Srivastava A K，Veldhuis S C.Modelling geometric and thermal errors in a five－axis CNC machine tool［J］.International Journal of Machine Tools and Manufacture，1995，35（9）:1321－1337.

［4］Yang S H，Kim K H，Park Y K.Error analysis and compensation for the volumetric errors of a vertical machining centre using a hemispherical helix ball bar test［J］.Int J Adv Manuf Technol.2004，23（2）:495－500.

［5］李晓丽.面向多体系统的五轴联动数控机床运动建模及几何误差分析研究［D］.成都:西南交通大学，2008.

［6］李圣怡，戴一帆，尹自强，等.精密和超精密机床精度建模技术［M］.长沙:国防科技大学出版社，2007.

［7］刘又午，章青，赵小松，等.基于多体理论模型的加工中心热误差补偿技术［J］.机械工程学报，2002，38（1）:127－130.

［8］辛立明，徐志刚，赵明扬，等.基于改进的多体系统误差建模理论的激光拼焊生产线运动误差模型［J］.机械工程学报，2010，46（2）:61－68.

［9］吴昊，杨建国，张宏韬，等.三轴数据铣床切削力引起的误差综合运动学建模［J］.中国机械工程，2008，19（16）:1908－1911.