数控机床伺服系统摩擦的非线性参数辨识研究*

陈光胜 李郝林

（上海理工大学机械工程学院，上海 200093）

伺服系统中的摩擦环节会使进给机构出现爬行、振荡，过象限突起以及较大的稳态误差等［1－2］。为实现伺服系统的高精度控制，在得到惯量、阻尼和摩擦等动态参数基础上对伺服系统进行精确建模是必要的。然而，仅利用设计参数通过解析法无法得到满意的结果。系统辨识是得到诸如摩擦类动态参数的有效的手段［3］。另外，由于进给机构运动部件润滑及磨损情况直接影响摩擦参数，因此对伺服系统的摩擦辨识也是实现机床性能评估和状态监测的需要。

尽管目前已有多个摩擦模型如:库仑+粘性模型［5］、Stribeck 模型［6］、Karnopp 模型［7］、LuGre 模型［8］和GMS［9］模型等。但Stribeck摩擦模型仍然是目前较为公认的成熟模型，由于该模型能对摩擦的静态特性能准确描述，因此在伺服系统的摩擦建模中被广泛采用。本文将针对数控机床的伺服系统，对进给系统运动机构中存在的摩擦进行研究，通过非线性辨识则到精确的Stribeck摩擦模型参数。

1 摩擦的Stribeck模型

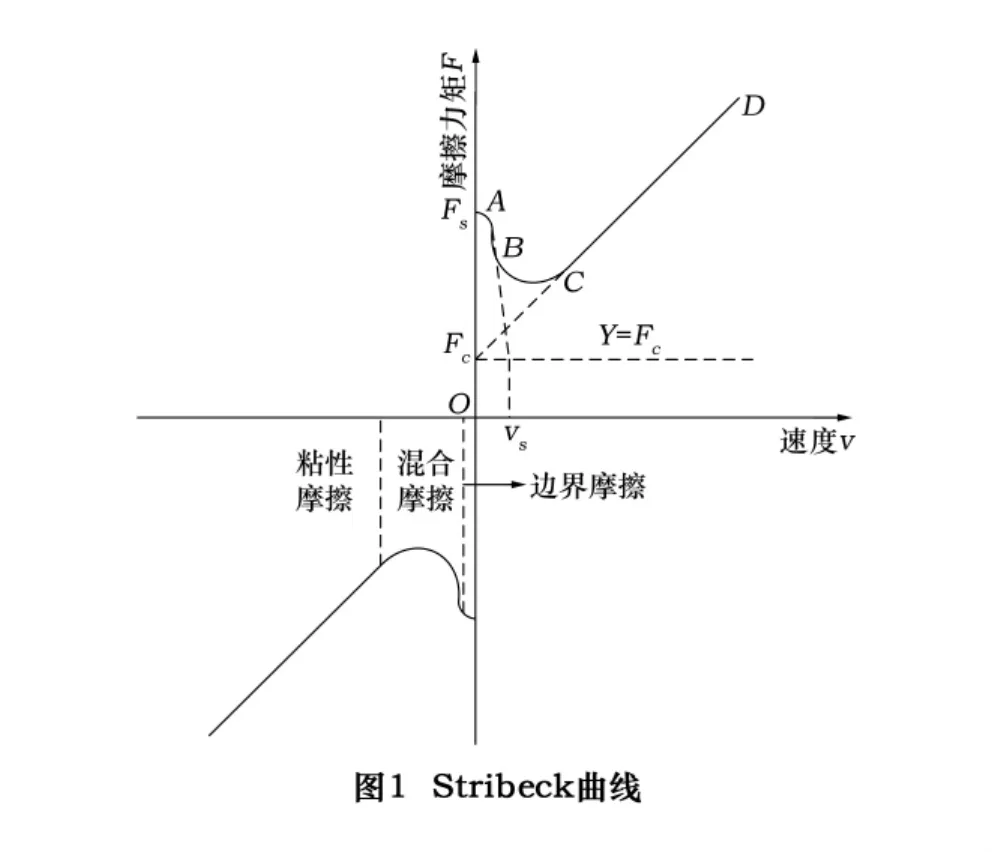
Stribeck模型也称“指数模型”，该模型由Stribeck在1902年提出。他研究发现，两物体间的摩擦力与相互接触物体表面之间的润滑油膜厚度有关，而接触面之间的润滑油膜厚度随着相对运动速度的变化而发生改变，因此摩擦力表现为相对运动速度的函数。这就是人们所熟知的Stribeck曲线，如图1所示。从Stribeck曲线可以看出，运动中的摩擦可以分为边界摩擦、混合摩擦和粘性摩擦3个阶段。在速度v较小时，随着速度的增加，静摩擦力逐渐以指数形式下降到库仑摩擦;而随速度v继续增大，粘滞摩擦力与速度成线性关系。在稳态运动时，摩擦力与速度的关系如下式:

式中:Fc为库仑摩擦力;Fs为静摩擦力;σ为粘滞摩擦因数;vs为临界Stribeck速度;δ为Stribeck形状系数，通常取1。Fc、Fs、σ和vs等参数需要通过参数辨识得到。

2 Stribeck模型参数非线性辨识

从式（1）可以看出，Stribeck模型为指数形式，因此无法利用线性的方法进行辨识，必须要实现非线性模型的线性化。

2.1 基本原理

将式（1）中指数项按泰勒公式展开，以6次为例，式（1）写成:

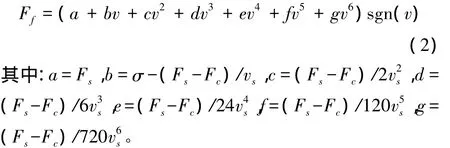
式（2）将摩擦力Ff写成了速度v的各次幂的线性表达式。当通过实验得到多组Ffi、vi序列时，令

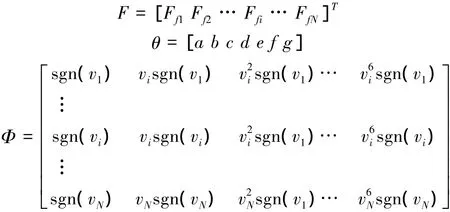
根据式（2），得

根据最小二乘法进行参数拟合，得到^θ，从而得到摩擦模型各参数

为了计算方便，在伺服电动机驱动的伺服系统中，摩擦力、速度也可以表示为Tf转矩（N·m）和ω转速（rad/s），这时，摩擦模型参数的单位也做相应调整。

2.2 实验曲线的获得

简化的伺服系统控制模型如图2所示，进给系统的移动部分和转动部分质量、阻尼、摩擦力均等效到伺服电动机的转动惯量Je、Be、Te

对于图2所示的模型，有

当机床工作台沿导轨匀速进给且空载运行时，电动机匀速转动，有˙ω=0，上式写成

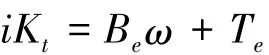
将阻尼力视为摩擦的一部分，这时

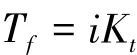
其中:Tf为机床在匀速进给时的摩擦力矩。

使机床伺服轴在不同速度下匀速空运转，通过信号采集系统得到电动机的电流i和转速n，即可得到电动机摩擦力矩Tf和转速n关系，并可换算为工作台进给速度v与摩擦力Ff的对应关系，并得到Stribeck曲线。

3 Stribeck模型参数非线性辨识实验

伺服系统的Stribeck模型参数辨识实验在某大型数控磨齿机砂轮修整系统进行，以对Y轴移动部件的摩擦为研究对象（图3）。Y轴伺服电动机扭矩常数Kt=1.1N/A，丝杠导程L=5 mm。

Y轴在空载情况下，采用不同的进给速度匀速往复进给，分别采集正向和反向进给时的电流值i和进给速度F。由于方法相同，本文仅以正向进给时的摩擦来研究，得到对应的摩擦力矩Tf和角速度ω的对应如表1所示，绘制的角速度与摩擦矩的离散点如图4所示。

表1 Y轴伺服系统正向进给时的速度与电流

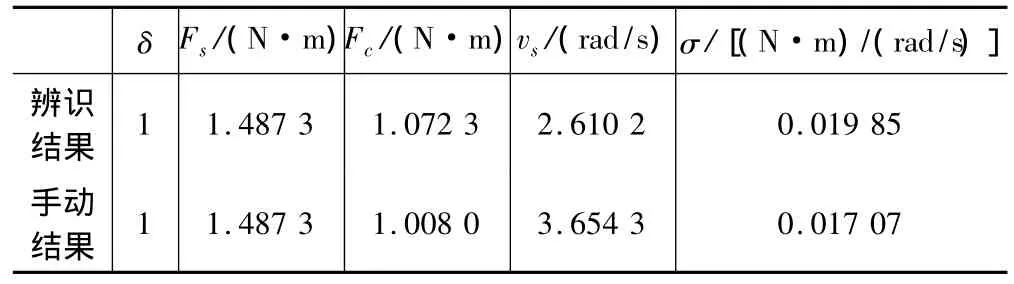
表2 Stribeck模型参数辨识结果

根据式（2）、（3），利用最小二乘法可以得到Stribeck摩擦模型的参数，在此基础上进一步手工调整得到优化的参数，利用优化后的参数能很好地拟合实验数据，如图4（实线）所示。辨识结果如表2所示。

4 结语

针对非线性的摩擦指数模型，提出用泰勒高次展开的方法达到摩擦模型的线性化，通过最小二乘拟合的方法得到摩擦模型的参数。为验证方法的有效性，针对数控机床进给系统移动部件进行了辨识实验，实验结果表明，该方法能对Stribeck摩擦模型的参数进行精确的辨识。该方法不仅适合于数控机床进给系统的静态建模，而且可以用于进给系统润滑或装配性能的评估，在工程应用中具有实用价值。

［1］Mei XS，Tsutsumi M，Tao T，et al.Study on the compensation of error by stick－slip for high－precision table［J］，International Journal of Machine Tools＆ Manufacture，2004，44:503－510.

［2］刘强，尔联洁，刘金琨，等.摩擦非线性环节的特性、建模与控制补偿综述［J］.系统工程与电子技术，2002，24（11）:45－59.

［3］Cohn S.Dynamic friction measurement，modeling，and compensation for precise motion control［D］.New Jersey:New Jersey Institute of Technology，1998.

［4］周玉清.基于无传感器信息的数控机床伺服进给系统性能评估研究［D］.西安:西安交通大学，2009.

［5］Zhang H J，Landers R G.Precision motion control methodology for complex contours［J］.Journal of Manufacturing Science and Engineering，Transactions of the ASME，2007，129（6）:1060－1068.

［6］Siciliano B，et al.Experimental Robotics VIII［M］，STAR 5，2003:328－337.

［7］Karnopp D.Computer simulation of stick slip friction in mechanical dynamic systems［J］.ASME Journal of Dynamic Systems，Measurement and Control，1985，107:100－103.

［8］Canudas D W C.A new model for control of systems with friction［J］.IEEE Tran.on Automatic Control，1995 ，40（3），419－425.

［9］F Al－Bender，Lampaert V，Swevers J，et al.The generalized maxwellslip model:a novel model for friction simulation and compensation［J］.IEEE Transactions On Automatic Control，2005，50（11）:1883－1887.