固定结合面法向静态特性模型研究*
2012-10-23张慧锋关立文李金峰
张慧锋 关立文 李金峰
(清华大学精密仪器与机械学系,北京 100084)
1 问题的提出
在机床中,固定结合面主要是指用螺栓连接的结合面,比如床身与立柱的连接,立柱与导轨的连接。研究表明,机床固定结合面刚度的数量级与材料本身的刚度相差1~2个数量级,所以固定结合面是机床刚度的一个薄弱环节;和机械零件本身的阻尼相比,结合面接触阻尼占有绝对优势,固定结合面接触阻尼是一个重要来源;结合面的非线性是机床结构非线性的主要来源,固定结合面的特性都呈非线性[1]。研究固定结合面对机床乃至各类机械都具有重要意义。
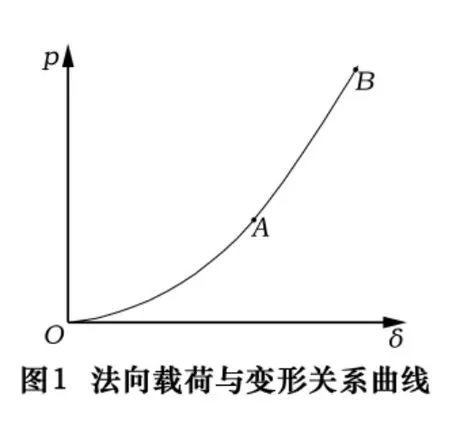
结合面的研究首先是从结合面的静态特性开始的,机床刚度是机床性能的重要指标,所以结合面的刚度是结合面静态特性的主要研究内容。结合面在受到载荷时发生变形,在这方面,很多学者都进行了研究,如 Levina[2-3]、Ostrovskii[4]、Dolbey 和 Bell[5]先后对相对较小的金属结合面进行了实验研究,结果表明,结合面的变形是结合面上法向压力的函数,具有非线性,且这种函数关系基本符合指数函数关系(如图1所示),并认为这种结合面变形是结合面上粗糙微凸峰的变形。
Thornley[6-7]提出的载荷 p 与结合面变形 d 的模型如下:

Levina[2-3]提出了一种相似的模型:

如果 C1、C2、C3、C4值选取合适的话,式(1)和式(2)表示的关系是类似的。此后有学者[8]应用式(2)中所示的关系,用指数关系模型拟合实验结果,能够满足工程需要。
以上两种对结合面变形与法向载荷的关系是在面压较小的情况下提出的,当结合面面压较大时,结合面变形与载荷曲线的曲率将变得很小,接近直线,如图1中的AB段。这样的拟合方法简单易行,操作方便,可以对实验结果进行较好的处理,为工程分析提供数据。
Thornley通过实验研究发现,在加载过程中,结合面法向变形包括弹性变形和塑性变形,卸载过程中只有弹性变形。而在卸载过程中,载荷较大时卸载曲线几乎呈直线,且刚度可以达到相同截面固体试件(无结合面的试件)的 90%[7]。因此可以认为,在载荷较大时结合面法向变形曲线是近似的直线。

表1 一组试件(钢-钢,铣-铣,50 mm×50 mm,粗糙度3.2 μm,无介质)实验数据
本文通过实验发现,如果只用指数模型拟合的话将出现较大误差。所以本文以实验为基础,在用指数曲线拟合数据结果的基础上,提出分段拟合的方法,以使拟合误差减小,为工程分析提供更高精度的数据。
2 固定结合面静态特性实验
组成结合面的两个试件如图2编号1和编号2所示,其中编号1是上试件,编号2是下试件。实验试件分为两组:第一组,材料为45钢,结合面粗糙度都是Ra3.2 μm,结合面名义接触面积分别有40 mm×40 mm,50 mm×50 mm,60 mm×60 mm,80 mm×80 mm,100 mm×100 mm;第二组,材料为铸铁,加工方法为铣削,结合面的名义接触面积都是40 mm×40 mm,结合面粗糙度分别为 Ra1.6 μm,3.2 μm,4.8 μm,6.4 μm,9.6 μm,12.5 μm。以上分组的目的是研究载荷、材料、粗糙度和面积对结合面法向刚度的影响规律。

试件的加工是在同一台铣床上进行,不同的粗糙度要求可以通过调整走刀量和切削速度来实现。由加工过程可知,试件面积越小,加工产生的平面度误差越小。当端面铣的刀盘直径一定时,如果试件的尺寸超过刀盘直径时,一个面需要走两刀或更多刀才能完成,这时的平面度误差比走一刀完成的大。结合面变形用至少两个传器测量,取平均值,以保证变形的准确。由于加载和卸载过程变形不重合,在加载过程中载荷应该保持单调,这样才能保证数据的可靠性。实验中采用龙门式加载,实验台如图2所示,图3为实验现场图。

3 实验结果及数据处理
实验结果主要以图和表的形式给出,如表1为第一组,尺寸为50 mm×50 mm的结合面法向位移和载荷的关系,对应的变形-载荷关系如图4所示。其他数据不再详细列出。
根据式(2)中结合面变形d与载荷p的关系:

所以结合面刚度k为

两边取对数,可以转化成线性关系
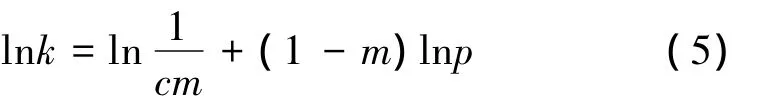
进行线性最小二乘拟合可以得到参数a和b,继而得到c和m。按照上述步骤对图4所示曲线进行拟合可得:法向变形 d=0.013 4p0.4508,法向刚度 kn=165.5p0.5492,拟合结果如图5a所示。其他数据部分拟合结果如图5b、c、d所示,剩余数据不再一一列出。
从上述实验数据和拟合结果可以看出,结合面法向变形随载荷变形基本符合指数曲线。在结合面面压较小时,结合面刚度非线性较强;结合面面压较大时,刚度的线性变得越来越强。这是由于在结合面面压较小时,实际接触的粗糙凸峰较少,单个凸峰所承受的压力较大,发生塑性变形;当载荷较大时实际接触的粗糙凸峰的数目增多,且已经发生塑性变形的粗糙凸峰的接触面积增大,使刚度增加。
4 分段模型
结合面变形与载荷的关系在理论上还没有形成明确的结论,学者们公认的关系是非线性的关系,在实际的处理过程中,大都处理成指数关系,通过实验验证,比较符合。
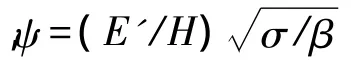
如实验结果(图5)所示,可以看出:在载荷较小时,变形曲线的曲率较大,用指数曲线的拟合也较好;在载荷较大时,变形曲线的曲率较小,这时与指数曲线的假设结果也出现明显的偏离。所以,综合实验结果与理论研究的结果,本文提出一种处理结合面变形与载荷的新的方法,即分段拟合的方法:在载较小时用系数曲线去拟合,载荷较大时,用直线去拟合,以使拟合误差减小。
分段拟合的拟合函数为
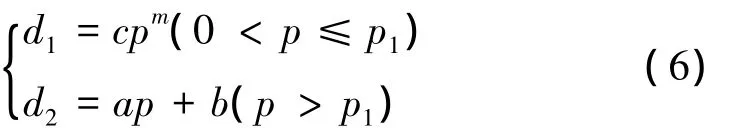
其中p1是分段拟合时的间断点。对表1所示数据进行拟合,拟合结果用公式表示为
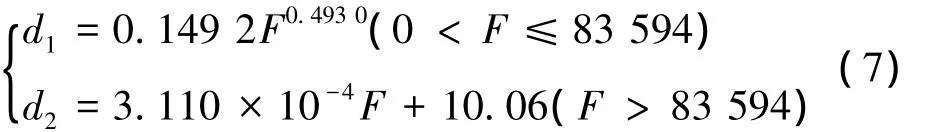
拟合结果图形如图6a左图所示。从图中可以看出,虽然拟合误差有所减小,但在两段曲线的连接点处,拟合曲线与实验点仍存在较大的误差。为此可以采用三段拟合,即在指数与直线中间加入过渡段,过渡段的拟合函数是指数曲线与直线的和,如下式

其中p1、p2分别是分段拟合时的间断点。对表1所示数据进行拟合,拟合结果为

拟合结果图形如图6a右图所示。其他数据部分拟合结果如图6b、c、d所示,剩余数据不再一一列出。
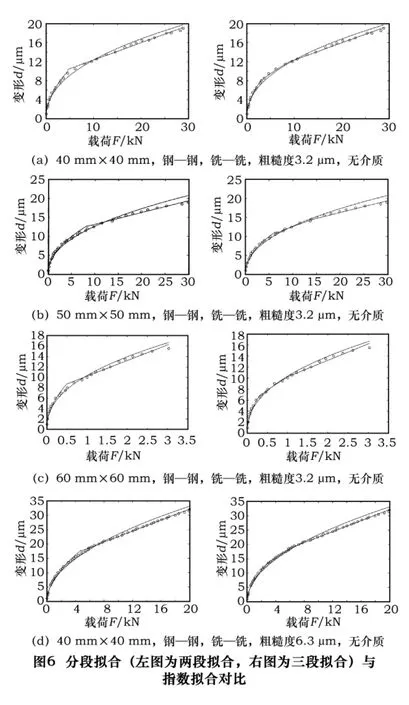

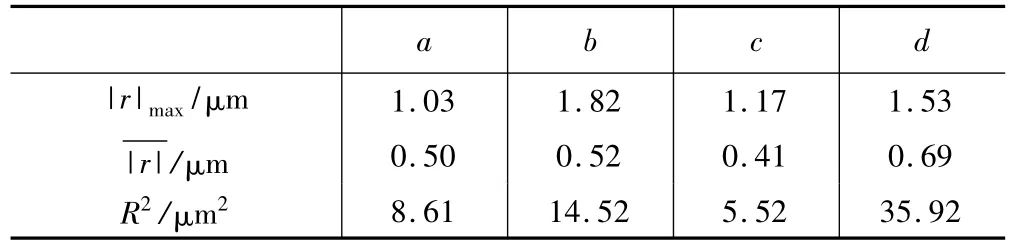
表2 指数拟合的拟合误差
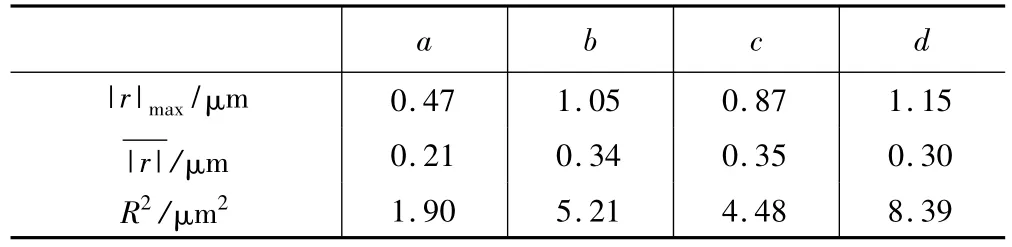
表3 分段拟合(两段)的拟合误差
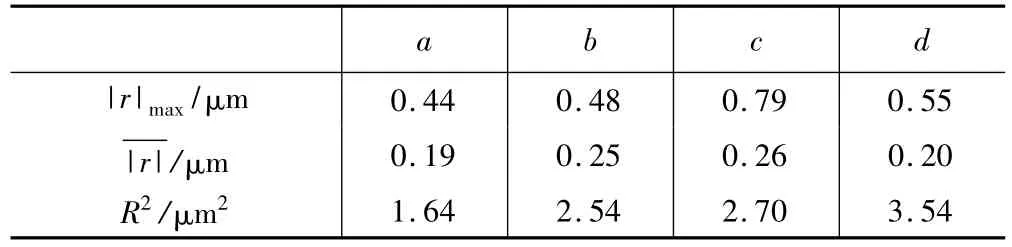
表4 分段拟合(三段)的拟合误差
对3种拟合模型的拟合误差对比如表5所示。通过表5可以看出,采用分段拟合方法后,拟合误差有显著减小。
表5 两种拟合方法误差()比较
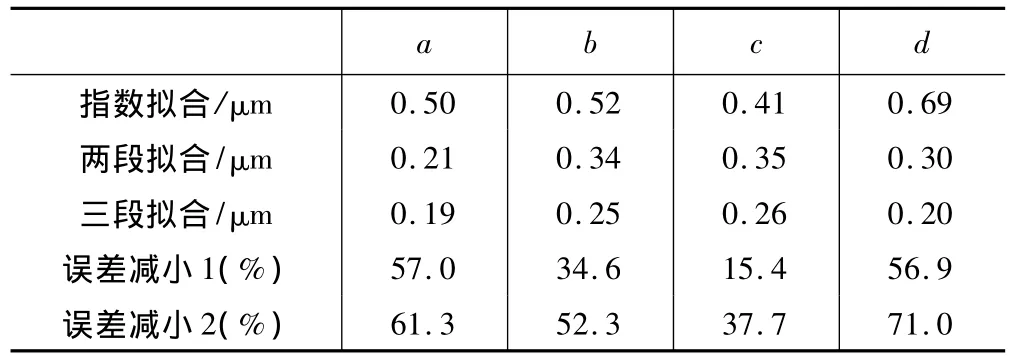
表5 两种拟合方法误差()比较
a b c d指数拟合/μm 0.50 0.52 0.41 0.69两段拟合/μm 0.21 0.34 0.35 0.30三段拟合/μm 0.19 0.25 0.26 0.20误差减小1(%) 57.0 34.6 15.4 56.9误差减小2(%) 61.3 52.3 37.7 71.0
5 结语
(1)分析了以往学者们对载荷-变形曲线拟合时所用的模型,指出了其优点;同时通过实验发现,这种模型与实验结果存在一定的误差。
(2)由结合面静态特性影响因素设计出结合面静态特性实验台,加工出了多组结合面试件,并进行了实验,得出可以被工程分析所利用的实验结果。
(3)研究了结合面法向变形随法向载荷的变化规律,用学者们使用较多的指数曲线进行了拟合,取得了较好的拟合效果。
(4)通过理论和实验分析,提出了一种新的拟合方法,即分段拟合的方法。与原来的指数拟合相对,减小了误差,能够为工程应用提供更高精度的刚度和变形数据。
[1]张学良.机械结合面动态特性及应用[M].中国科学技术出版社.2002.
[2]Levina Z M.Calculation of contact deformations in slideways[J].Machine and Tooling,1965,36(1):128.
[3]Levina Z M.Research on the static stiffness of joints in machine tools[C].Proc.8th Confer.M.T.D.R.,1967.
[4]Ostrovskii V I.The influence of machining methods on slideway contact stiffness ,machine and tooling[J].1965,36(1):9217.
[5]Dolbey M P,Bell R.The contact stiffness of joints at low apparent interface pressure[C].Annals of CIRP,1970.
[6]Thornley R H,Connlly R,Barash M M,et al.The effect of surface topography upon the static stiffness of machine tool joints[J].Intern.J.M.T.D.R.,1965(5):57-74.
[7]Thornley R H,Connlly R,Barash M M,et al.The effect of flatness of joint faces upon the static stiffness of machine tool joints[J].Proc.Inst.Mech.Engrs.,1967(182):463-476.
[8]黄玉美,佟淑贤,秦世良.机床结构设计效果预断中结合条件的处理方法[J].机床,1990(6):8-12.
[9]Greenwood J A,Williamson J B P.Contact of nominally flat surfaces[J].Proc Roy Soc Lond,1966,A295:300-319.
[10]Majumdar A,Bhushan B.Fractal model of elastic-plastic contact between rough surfaces[J].J Tribol(ASME),1991,113:1-11.
