基于量测自适应辨识的多传感器数据融合算法*
2012-10-22胡振涛贾培燕付春玲杜海顺
胡振涛,贾培燕,付春玲,杜海顺
(1.河南大学 图像处理与模式识别研究所,河南开封 475004;2.河南大学基础实验教学中心,河南开封 475004)
0 引言
多传感器信息融合相对于单个传感器所获得的信息具有冗余性、互补性,从而进一步增强了估计结果可靠性和鲁棒性。在结构上一般分为集中式、分布式、混合式和多级式,后2种结构形式实际上是在集中式和分布式基础上的拓展,针对具体被估计对象特点,可通过集中式和分布式优化组合实现[1,2]。近年来,针对集中式和分布式融合框架,在系统估计实现中已取得较为丰富的成果,但现有结论成立的前提是对被估计系统的精确建模,即已知系统或量测的部分先验统计信息。然而,在实际工程环境中,一些外界扰动(传输误差、计算误差、环境噪声和人为干扰等)是无法回避的,使得建模噪声和实际噪声的统计特性具有较大偏差,而这种偏差直接影响着滤波器估计精度[3,4]。因此,在量测不确定条件下研究如何利用多传感器量测数据实现复杂混合系统状态估计具有重要的现实意义。对于含扰动影响量测数据的辨识和剔除一般采用离线处理的方式,这种方式通常和滤波器设计之间是孤立的[5,6]。近年来,基于线性最小方差估计准则的Kalman滤波(KF)架构上发展起来残差检测方法,但需要利用先验信息实现野值检验门限的设定,限制其应用范围[7]。
基于以上分析,结合KF技术,本文给出了一种量测不确定下多传感器自适应数据融合(MAKF)算法。在与滤波器结构有效结合的情况下,自适应实现了含扰动影响量测数据剔除和无扰动影响量测数据的融合。仿真实验结果表明:在扰动对量测影响显著的情况下,MAKF的滤波估计精度明显优于集中式量测最优加权融合(M-KF)算法以及分布式状态最优加权融合(S-KF)算法,并且实时性方法相对于分布式状态最优加权融合算法获得了显著提升。
1 MAKF算法
量测不确定条件下,对复杂混合系统估计中无论采用集中式或分布式结构下都必然将导致以下问题:融合中心所处理的信息都不可避免包含了整个采样过程中所有扰动的影响;另外,分布式结构中由于通过每个处理节点首先独立完成状态估计,将导致计算复杂度的急剧增大,特别在多模型系统中这种影响更为显著。如何实现对于随机扰动的剔除,自适应在线选取有效量测(即无扰动影响的传感器量测)是提升系统估计精度的核心问题。
1.1 基于量测精度加权融合方法
量测精度加权融合方式主要应用于多传感器信息融合系统的集中式处理结构中。该结构的特点是将各个信源的量测传递到融合中心,由融合中心统一进行融合处理,处理对象一般是多传感器得到被估计对象的原始量测信息。在多传感器集中式处理结构下,满足无偏且方差最小估计意义下各传感器权重表达式为

式中 σk,m为传感器m自身的量测精度,融合后量测精度为


1.2 基于滤波误差协方差加权融合方法
滤波误差协方差加权融合主要应用于多传感器信息融合系统的分布式处理结构中,该结构的特点是在各个信源的量测传递给融合中心以前,先依据自身的数据处理器进行滤波处理,融合中心处理的对象则一般是局部状态估计结果。已知k时刻各局部滤波器状态无偏最小方差估计^Xk/k,m和滤波误差协方差阵 Pk,k,m,且各局部状态估计值在全局估计中的权重为
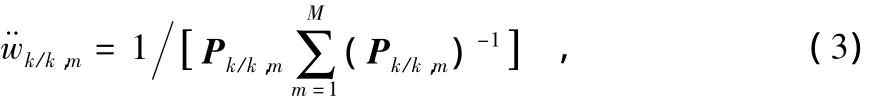
则全局最优估计可表示为


1.3 传感器量测自适应辨识策略
首先,结合k时刻量测一步预测值分别计算传感器的量测似然度 ℓk,m,并基于 ℓk,m最大化原则,实现不含扰动影响传感器量测的辨识
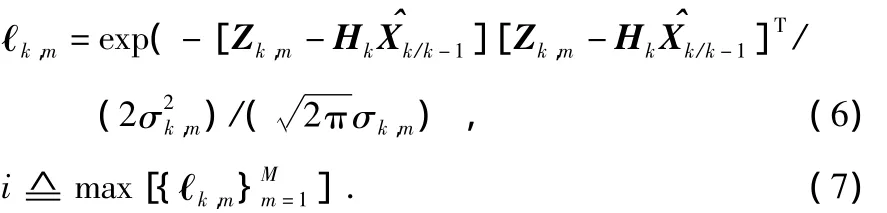


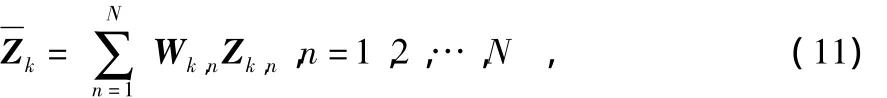


2 仿真结果分析
为验证算法的可行性和有效性,仿真场景设定为采用精度不同的雷达量测数据实现对于X-Y平面上运动目标的跟踪,并且分别在确定性扰动和随机性扰动2种情况下比较了M-KF,S-KF和MAKF三种算法状态估计结果。目标运动状态演化和量测演化方程如下
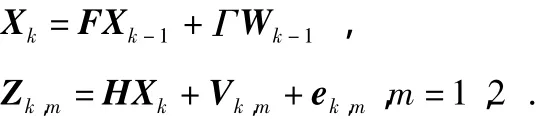
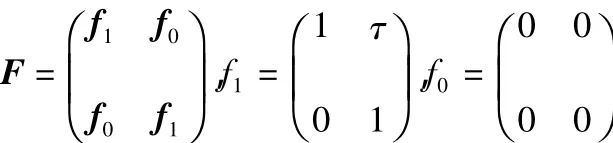
图1(a)给出了确定性扰动场景下Monte-Carlo仿真中第20次量测模型的辨识结果。纵坐标中的1和2分别表示雷达1无外界扰动影响与有外界扰动影响下量测模型状态;3和4分别表示雷达2无外界扰动影响与有外界扰动影响下量测模型状态;2.5表示利用MAKF算法判定雷达1和雷达2均不受到外界扰动影响下量测模型状态。由图中结果可知,在确定性扰动下,MAKF中仅在第11个采样时刻采用了含扰动影响的雷达1的量测数据,而滤波过程其他采样时刻的有效量测均采用了无扰动影响的雷达量测数据。并且在1~5和16~25个采样时刻准确地识别出两雷达数据均不含扰动影响,这与预先设定的场景是相符的。这种雷达量测选取方式对于滤波估计精度的影响可以通过图2(a)和图2(b)得到进一步验证,即6~15个采样时刻和26~35个采样时刻,M-KF和S-KF算法的均方根误差(RMSE)远远大于MAKF算法,由上面量测模型的辨识结果可知,这种结果产生的主要原因是MAKF算法利用的量测均为无扰动影响的雷达量测数据。而在1~5和16~25个采样时刻 M-KF和S-KF算法的滤波精度与MAKF算法相接近,主要是以上采样时刻系统中雷达量测均不受扰动的影响,此时利用M-KF和S-KF算法也能够实现滤波精度的改善,MAKF算法本身由于实现雷达量测有无扰动影响的正确判别,并在扰动数据剔除情况下结合了集中式量测最优加权融合方式,从而使得滤波精度接近M-KF和S-KF算法。此外,MAKF算法的性能优势可进一步通过表1中给出的定量分析数据得到反映。
图1(b)给出了随机性扰动场景下Monte-Carlo仿真中第20次量测模型的辨识结果,图中纵坐标各点代表的含义和图1相同。图3(a)和图3(b)则给出了3种算法在滤波精度上结果比较。对于量测模型的误判率和滤波精度可以从表1中统计数据中得到清晰的反映。以上结果验证了在随机性扰动条件下,MAKF算法得到量测模型的误判率和滤波精度同样优于M-KF算法和S-KF算法。

表1 基于50次Monte—Carlo仿真条件下RMSE的均值Tab 1 Mean of RMSE based on 50 times Monte-Carlo simulation condition

图1 量测模型辨识Fig 1 Measurement model identification

图2 确定性扰动下位置估计RMSEFig 2 RMSE of position estimation in certainty disturbance

图3 随机扰动下位置估计RMSEFig 3 RMSE of position estimation in random disturbance
3 结论
针对量测不确定下多传感器融合系统的状态估计问题,本文给出了一种MAKT算法。相对现有处理方法,新算法具有以下优势:首先,算法构建以多传感器数据融合理论为基础,可充分利用多传感器量测中冗余和互补信息,提升系统状态估计结果的可靠性和鲁棒性。其次,实现对于受扰动影响量测数据在线辨识,使得MAKF算法具有较好的滤波精度。最后,MAKF算法对于扰动处理方式避免了对于先验信息的依赖,且物理含义明确、算法实现简单。
[1] Julier S J.Estimating and exploiting the degree of independent in-formation in distributed data fusion[C]∥12th International Conference on Information Fusion,2009:772 -779.
[2] Mahler R P S.Statistical multisource-multitarget information fusion[M].Boston,London:Artech House Publishers,2007.
[3] Ting J A,Theodorou E,Schaal S.A Kalman filter for robust outlier detection[C]∥IEEE/RSJ International Conference on Intelligent Robots and Systems,2007:1514 -1519.
[4] Shuai M,Xie K Q,Chen G H,et al.A Kalman filter-based approach for outlier detection in sensor networks[C]∥International Conference on Computer Science and Software Engineering,2008:154-157.
[5] Angiulli F,Basta S,Pizzuti C.Distance-based detection and prediction of outliers[J].IEEE Transactions on Knowledge and Data Engineering,2006,18(2):145 -160.
[6] Yousri N A,Ismail M A,Kamel M S.Fuzzy outlier analysis a combined clustering-outlier detection approach[C]∥IEEE International Conference on Systems,Man and Cybernetics,2007:412 -418
[7] Abdelhadi B,Benoudjit A,Nait-said N.Application of genetic algorithm with a novel adaptive scheme for the identification of induction machine parameters[J].IEEE Transactions on Energy Conversion,2005,20(3):284 -291.
[8] Soonho J,Tugnait J K.Tracking of two targets in clutter with possibly unresolved measurements[J].IEEE Trans on Aerospace and Electronic Systems,2008,44(2):748 -765.
