穿舱爆炸舰船局部毁伤效果模型实验方案研究*

王奂钧，王 超，岳永威，苏罗青，陈海龙，2

（1．哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨 150001;2．哈尔滨工业大学航天学院，黑龙江 哈尔滨 150001;3．广州船舶及海洋工程设计研究院，广东广州 510250）

0 引言

随着各国军事科技的迅猛发展，现代海战的发展趋于空间化、立体化，舰船在战斗或执行任务中极易遭受到来自空中反舰武器攻击［1］。

目前国内外许多学者在评估舰船穿舱爆炸载荷作用下的毁伤效果［2，3］方面，基本上采用大尺度缩比原模型或全尺寸局部模型开展爆炸实验来评估。然而，由于载荷相似规律和最佳缩尺比选择还没有形成体系，因此，模型实验结果难以准确评估原型船的毁伤效果。在舰船穿舱爆炸毁伤效果实验中，如果能够得到准确的载荷转换相似规律，采用准确的模型缩比系数，以完全相似模型为母型，根据弹性畸变准则，选择合适的畸变系数对完全相似模型生产困难大的板架结构进行畸变等效转换，使用等效转换处理后的模型进行实验。这样，降低了模型在生产建造中难度的同时，还可以在提高实验成本经济性的前提下，准确得到原舰船结构遭受穿舱爆炸载荷时动态响应。本文采用爆炸冲击波在空气中传播的相似律、冲击波舱室内反射相似律为载荷加载的等效，并利用准确的结构弹性畸变准则对母型船结构进行畸变，通过数值仿真计算手段得到满足工程精度、生产加工难度，经济性等要求的舰船结构缩比模型实验方案。

1 缩比模型穿舱爆炸相似规律

多年来，国内外许多学者一直在爆炸“相似律”领域进行探索与研究，寻求利用大尺度缩比模型实验的方法预测母型结构动响应特性，迄今为止取得了许多的学术成果［4，5］。穿舱爆炸对船体结构毁伤作用是一个很复杂的物理过程，分为爆轰波膨胀和作用结构使其产生毁伤2个阶段，结构的材料特性也会随着冲击载荷的时历变化发生不同，如果简单地应用完全相似准则处理爆轰和结构特性，得到的实验数据结论将与原型发生较大偏差，甚至部分或完全背离。因此，需要对穿舱爆炸产生的爆轰波和结构材料在不同特性的载荷作用下相似律分别讨论。另外在实际应用中，由于生产加工的难度，使按完全相似律建造的模型无法实现，因此，就必须利用结构弹性畸变准则对与原型评估结果吻合度较高的完全相似模型作为母型模型，并对其进行等效转换得到畸变相似模型，最终得到对原型毁伤效果的准确评估结果。

1．1 爆轰波与冲击波载荷相似律

反舰武器爆炸产生爆轰波与冲击波的作用具有瞬态性和很强的冲量，分析其在空气场中的传播规律认为其相似规律与空气中冲击波相似规律有着很高的吻合度。本文假设爆轰波未作用至舱室结构时在密闭舱室的传播规律在自由场中传播规律相同，要使爆轰产物的膨胀过程相似，必须使各基本相似量间满足一定的相似条件，即

式中p0为空气初始状态的压力，ρo为空气初始状态密度;E0为炸药能量;r为爆炸冲击波的传播距离，可根据量纲统一建立方程组求出，最终分析得到各物理量与基本物理量之间的函数关系［6］

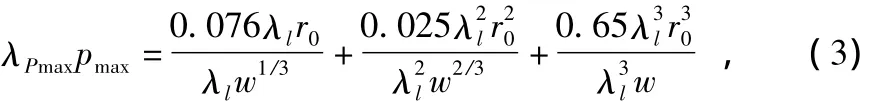
即可得

式中 τ+为冲击波正压作用时间，利用经验公式和相似比关系［8］可以推导出

即可得

式中 λl为结构特征长度缩比，λPmax为爆轰波与冲击波压力峰值缩比。

应用上述方法推导可得λE=λρ=λl，当缩比实验模型的几何尺寸与载荷的加载形式和原模型完全相似时，两者冲击波超压峰值是相同的，而表征冲击波特性的其他参数将按特征长度相似常数（λl）求解。

1．2 冲击波舱室内反射相似律

反舰武器战斗部穿舱爆炸形成的冲击波在与舱壁作用的同时，将在舱室内发生若干次反射，因而，在考虑穿舱爆炸实验方案时应考虑冲击波的反射效应。本文应用声学理论中室内混响的计算方法建立冲击波在舱室内反射的计算模型。根据该模型可得

可得

正压作用时间相似率由以下公式确定

可得

1．3 舰船模型完全几何相似律

为使缩比舱室结构在穿舱载荷作用下的最终变形与原型呈完全几何相似，因而，应用塑性动力学中刚塑性方板在均布载荷作用下的动态响应计算模型为基础计算舰船模型完全几何相似律。由该模型可得

可得

根据载荷特性的不同，将载荷分为2种情况计算:

当p0＜p≤2p0时，为中载情况，结构的挠度相似律为

可得

当p＞2p0时，为高载情况，结构的挠度相似律为

其中，θ0，λθ分别由以下两式求得

1．4 舰船模型畸变相似准则

在缩比模型生产过程中，某些情况下，采用完全相似准则制定的生产工艺实现困难，如模型中的小尺寸构件按完全相似缩比尺寸进行缩比，使模型在生产加工过程中会产生诸多困难，因此，须应用畸变模型。畸变模型是以完全相似模型为母型模型，对完全相似模型某些构件的1个或几个参数进行放大，在保证对原型动响应特性的评估不产生很大影响的前提下，满足生产加工的要求。

又因为对于基准模型和畸变模型，有相似常数λP（t）=1，λμ=1，所以

将T型梁畸变等效为截面矩形的梁［11，12］，当截面矩形的惯性矩、梁剖面积和抗弯截面模量与原型T型梁最接近时，此等效模型的动力学特性与原型最为接近，更重要的是，采用此畸变的模型更便于生产加工。

2 计算结果分析

2．1 模型与实验计算工况设定

本文以XXX舰有限元模型为原型，选取攻击武器为YX-X型反舰导弹（见图1）空爆实验工况为例即由船体舷侧穿舱并于舱室内爆炸，装药质量相当于m=Mkg的TNT，探究XXX舰此典型工况下的毁伤效果。坐标原点位于船体舯横剖面、舯纵剖面与船底板的交点。x方向为船长方向（正方向为船舯横剖面指向船艏方向），y方向为船宽方向（正方向为船舯纵剖面指向船体左舷），z方向为船高方向。为了评估缩比模型与原型动态响应的相似度，本文选取了延z方向相对位置处选取4处典型考核点进行考核，输出局部MISES应力时历曲线。

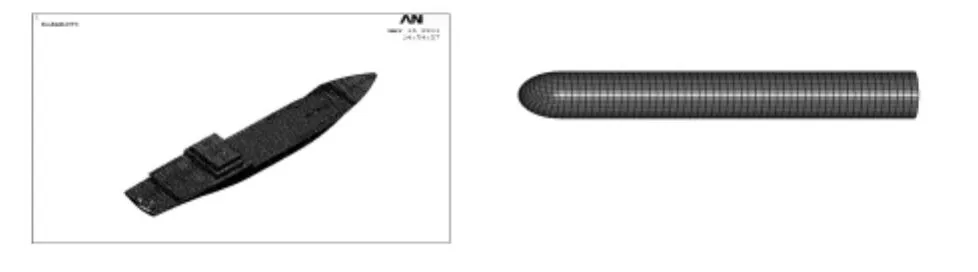
图1 XXX舰及其YX-X型反舰导弹有限元模型Fig 1 Finite element model of the warship and YX-X type anti-ship missile

2．2 完全几何相似模型实验方案

为了得到最佳的缩比模型，本文提出5种完全缩比模型与原型进行数值实验，并比较分析其计算结构，舱室内爆炸载荷的等效采用自由场载荷相似理论。实验模型原型与缩比模型相似关系如表1所示。

表1 XXX型舰原型与模型相似关系Tab 1 Similarity relationship between the XXX type warship and model

下面分别给出XXX舰及其缩比模型遭受穿舱爆炸载荷作用各个考核点的无量纲MISES应力时历对比曲线，缩比模型的MISES应力按结构变形相似常数λw换算，缩比模型的时间按长度相似常数λl换算，计算结果如图2～图5。

图2 船底板Mises应力时历曲线Fig 2 History curves of Mises stress of bottom plate

图3 中底桁Mises应力时历曲线Fig 3 History curves of Mises stress for bottom central stringer plate

图4 旁底桁Mises应力时历曲线Fig 4 History curves of Mises stress for bottom nearby stringer plate

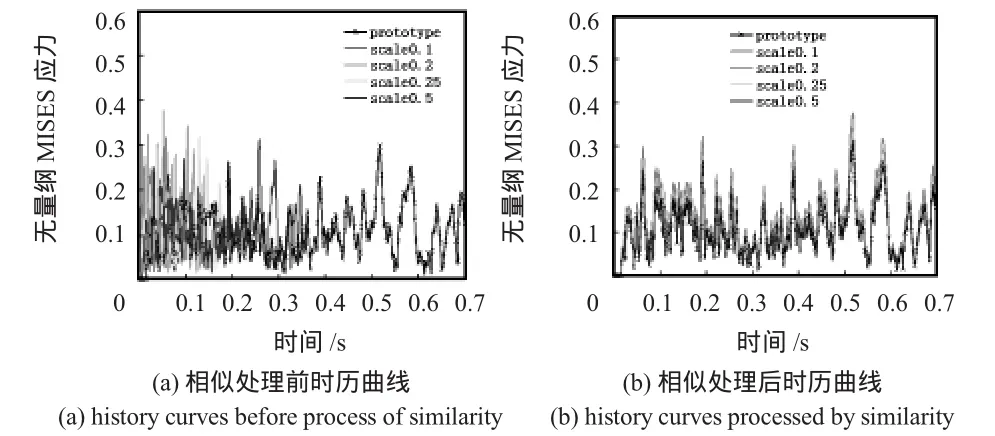
图5 主甲板Mises应力时历曲线Fig 5 History curves of Mises stress for bottom main deck

从上图可以看出:应用舱室内爆炸相似理论制定实验方案得到的各相似模型MISES应力时历曲线基本吻合。应用完全几何相似模型制定实验方案得到的数值实验结果，可以很准确地评估原型结构的动态响应特性。

综合考虑各相关因素，选取缩尺比λ=0．25作为模型的相似准数。

2．3 畸变模型实验方案

本文选取缩尺比为λ=0．25的模型为母型，将其板架结构上的型梁畸变等效转换为矩形截面梁，母型中板厚小于5 mm的船体板的板厚以0．5h为增量从h～5h变化，对这8种不同畸变系数的模型分别进行数值实验，得到最为合适的畸变模型实验方案。

数值实验结果表明:当畸变系数φ=2．5时，畸变模型与母型的试验结果的吻合性最高。下面给出当畸变系数φ=2．5时，XXX舰的母型模型与φ=2．5的畸变模型遭受舱室内爆炸载荷作用下，各考核点相似前和相似后无量纲MISES应力时历曲线对比，如图6～图9所示。

图6 船底板Mises应力时历曲线Fig 6 History curves of Mises stress for bottom plate

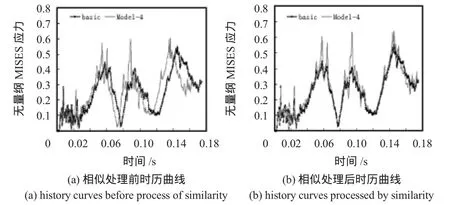
图7 中底桁Mises应力时历曲线Fig 7 History curves of Mises stress for bottom central stringer plate

图8 旁底桁Mises应力时历曲线Fig 8 History curves of Mises stress for bottom nearby stringer plate

图9 主甲板Mises应力时历曲线Fig 9 History curves of Mises stress for bottom main deck

从上图中可知，经过畸变等效的畸变模型考核点MISES应力时历曲线与原型的有很好的吻合度，以误差为15%作为评估标准，即可认为选取缩尺比λ=0．25，畸变系数φ=2．5时，畸变模型可以对母型的在穿舱爆炸载荷作用下的动态响应进行评估，畸变实验模型评估如表2。

表2 畸变实验模型评估表Tab 2 Estimation sheet of distorted experimental model

3 结论

1）针对舱室内爆炸作用下舰船实验提出了5种完全相似缩比实验方案，综合考虑模型生产加工的可操作性和实验成本的经济性，确定缩尺比λ=0．25作为模型的特征长度相似比。

2）应用完全几何相似模型，可以得到与原型结构吻合度很高的计算结果，可准确地评估原型遭受舱室内爆炸载荷时的结构动响应特性。

3）选定缩尺比λ=0．25、畸变系数φ=2．5作为最佳实验方案，可较为准确地预测原模型的动态响应，实现了实验准确性、模型生产加工可操纵性和实验成本的经济性。

［1］ 汪 玉．舰船现代冲击理论及应用［M］．北京:科学出版社，2005:21－29．

［2］ 徐培誉．水下爆震对结构之响应［D］．台北:台湾大学，2004:2－12．

［3］ Keil K A．The response of ship to underwater explosion［J］．SNAME，1961，69（4）:5 －7．

［4］ 程素秋，宁永成，张臣，等．相似理论在水下爆炸模型实验中的应用［J］．船舶科学技术，2008，30（3）:96 －99．

［5］ 张 亮，李云波．流体力学［M］．哈尔滨:哈尔滨工程大学出版社，2007:179－187．

［6］ 张效慈．水下爆炸实验相似准则［J］．船舶力学，2007，2（1）:108－118．

［7］ 库尔·P．水下爆炸［M］．罗耀杰，译．北京:国防工业出版社，1960:17－20．

［8］ Klaseboer E，Khoo B C，Hung K C．Dynamics of an oscillating bubble near a floating structure［J］．Journal of Fluid and Structure，2005，21:395 －412．

［9］ 苏罗青．舰船总体与局部强度水下爆炸实验方案研究［D］．哈尔滨:哈尔滨工程大学，2011:25－47．

［10］张海鹏，岳永威，苏罗青．水下爆炸作用下舰船总纵强度模型实验方案研究［J］．振动与冲击，2012，31（6）:175 －180．

［11］徐挺著．相似方法及其应用［M］．北京:机械工程出版社，1995:18－20．

［12］谢建林．瞬态载荷作用下弹塑性结构动响应相似性研究［D］．哈尔滨:哈尔滨工程大学，2008:24－55