考虑流固耦合的水位降落期坝坡稳定分析

田 江 沈长松 王栋良

（1.河海大学 水利水电学院，南京 210098；2.中国水电顾问集团 华东勘测设计研究院，杭州 310014）

我国已建成的各类水库有8万多座，但绝大部分兴建于20世纪50～70年代，限于当时的技术和经济条件，水库设计标准偏低、施工质量差，经过多年运行存在各种安全隐患，急需对其进行除险加固.目前，小（Ⅱ）型病险水库除险加固工作在全国范围内有条不紊地进行着，水位降落期的土石坝坝坡稳定分析是除险加固工程中的重要内容之一.因此，选取合理的计算方法来分析水位降落时上游坝坡的稳定性具有重要的实际意义.

目前，水位降落期的坝坡稳定分析一般采用传统的极限平衡法［1－2］，该方法主要基于非稳定渗流计算原理和极限平衡原理.首先进行水位降落期非稳定渗流计算，然后把不同时刻的孔隙水压力大小应用于极限平衡法，从而计算不同时刻的最小稳定系数.该方法除了没有考虑应力变化对渗流的影响外，还具有极限平衡法自身的缺点，如将土体看作刚体，忽略土体的应力和变形的关系，这给计算结果带来一定的误差.

此外，以强度折减法为代表的有限元方法已用于水位降落期坝坡稳定分析中［3－4］，该方法基于材料参数的强度折减原理，并克服了极限平衡法不能考虑土体自身变形对坝坡稳定的影响等缺点，但其临界破坏的判断准则还有一定的争议.除了以强度折减法为代表的有限元法外，还有以有限元计算的应力分布结果为基础，通过张量变换计算出假定滑动面上的稳定系数［5－6］，但这种方法在同时考虑非饱和土流固耦合的影响研究则较少.

水位快速降落过程中，对于渗透系数较小的均质坝，作用于其上游坝坡的水压力快速消失，而坝体中的超静孔隙水压力消散较慢，降落前的饱和区域变成非饱和区域，这本质上是一个非饱和土的固结问题.本文以某病险水库为例，以非饱和土流固耦合理论和有限元极限平衡法原理为基础，对水位降落期上游坝坡进行稳定性分析.首先根据有限元模型进行非饱和土渗流－应力耦合计算，再根据计算所得各时刻的应力与孔隙水压力结果进行边坡稳定分析，并与传统的极限平衡方法进行了对比，得出一些有价值的结论.

1 基本理论

1.1 非饱和土流固耦合理论［7］

1）渗流方程

根据Darcy定律，非饱和土的二维渗流方程可表示为

式中，kx，ky分别表示x和y方向的渗透系数；uw为孔隙水压力；γw为单位水的重量；θw为体积含水率；t为时间.

2）土体本构方程

假设气压在整个非饱和区保持恒定，等于大气压力，则非饱和土应力－应变增量形式可以写成以下形式：

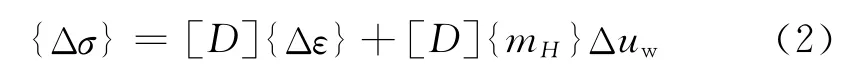
3）有限元平衡方程

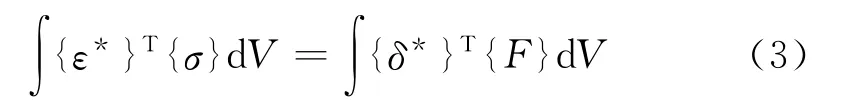
应用虚功原理，并分别对公式（1）和公式（2）进行离散，最后耦合方程可以写成下列形式：

1.2 有限元极限平衡法原理

有限元极限平衡法是以有限元法计算的应力为基础，通过张量变换方法把高斯点上的应力转化成假定滑动面上各微段的正应力和剪应力，求解滑动面的稳定系数，运用极限平衡法中滑动面搜索方法可以求出最小稳定系数.该方法避免了传统极限平衡法中的许多假设，计算出的应力更加贴合实际，此时坝坡的稳定系数可按如下公式计算［8］：

式中，∑Sr为沿整个滑面总的最大抗剪力，∑Sm为沿整个滑面总的下滑力.

本文采用基于 Mohr－Coulomb屈服准则的理想弹塑性土体本构模型，以非饱和土流固耦合的应力结果为基础，求得不同时刻的最小稳定系数.在分析中同时考虑了基质吸力对坝坡稳定的影响，故微小滑弧段的抗剪力和下滑力可表达为：

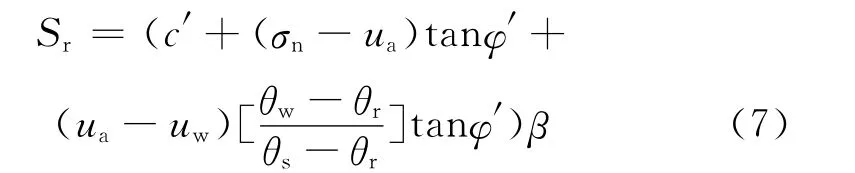
式中，β为条块底面长度；c′为有效粘聚力；φ′为有效内摩擦角；ua为孔隙气压力；uw为孔隙水压力；θw为体积含水率；θs为饱和体积含水率；θr为残余体积含水率；σn为条块底面中心正应力；τm为条块底面中心剪应力.

2 工程实例及分析

2.1 计算模型及计算参数

某小（Ⅱ）型水库，大坝为均质土坝，坝顶高程为84.20m，坝顶宽度为3.0m，上下游坝坡均为1∶2.5，上游正常蓄水位80.6m，死水位为72.6m，设计洪水位81.76m，校核洪水位82.96m，下游79m高程处设有6m宽平台.坝体料为粉质粘土，坝基为强风化千枚岩.大坝无排水措施，下游出溢点较高，渗漏现象严重，故需对其进行坝坡稳定分析，本文只对其进行水位降落期上游坝坡的稳定分析.

选取大坝最大断面作为计算典型断面，大坝分区和网格剖分如图1所示.

图1 典型剖面及网格剖分图

耦合计算时需要给定位移边界条件和水力边界条件，位移边界条件为地基左右两侧水平向约束，底部固向约束，坝坡面为自由面；水力边界条件为上下游均为已知水头.为了解上游水位降落速度对上游坝坡稳定的影响，分析了水库水位分别以不同的速度从校核洪水位82.96m降落至死水位72.60m后水位保持不变不同工况下的坝坡稳定性.工况1、工况2和工况3依次为1.0m／d、2.0m／d和3.0m／d的速度从校核洪水位降落至死水位.

大坝各个分区的材料参数根据地勘资料并参考类似工程选取，具体见表1.

表1 坝体物理力学参数

坝体填筑料为粉质粘土，本次计算采用的粉质粘土的土－水特征曲线是根据其饱和体积含水率和残余体积含水率，由GeoStudio软件中内置的粉质粘土的土－水特征曲线实验数据拟合得到，如图2所示；基质吸力与渗透系数的关系曲线则根据Van Genuchten模型估算得出，如图3所示.

图2 土－水特征曲线

图3 基质吸力与渗透系数的关系曲线

2.2 计算结果及其分析

1）上游水位降落速度对坝坡稳定系数的影响

图4为水位降落至死水位时刻3种工况下坝体内浸润线的位置，坝体内孔隙水压力的消散速度明显低于上游水位的下降速度，这就形成了“逆流”现象，不利于上游坝坡的稳定.图5反映了不同工况下上游坝坡最小稳定系数随时间的变化规律，都呈现先下降后慢慢上升的趋势.上游水位降落越快，坝坡最小稳定系数降落也越快，最小稳定系数随着降落速度的增大而减小，主要是因为水位降落速度越快，降落至死水位时间越短，坝体内的孔隙水消散时间相对缩短，“逆流”现象越严重.

2）基质吸力对坝坡稳定的影响

基质吸力对坝坡稳定性的影响程度与坝体中非饱和区域的大小有关，从表2和图4分析可知，由于初始状态坝体内的饱和区域很大，当水位降落过快，坝体渗透系数较小时，坝体内的超静孔隙消散很慢，水位降落至死水位时坝体内形成的相对非饱和区域很小，此时，降落期基质吸力对坝坡稳定的影响相对较小.因此，是否考虑基质吸力对坝坡稳定的影响可根据实际工程在水位降落工程中坝体内非饱和区域的大小而定.

表2 最小稳定系数对比

3）耦合与非耦合情况下的计算结果对比

如何精确确定坝体中孔隙水压力的分布情况是水位降落期坝坡稳定分析的一个重要问题.以工况1为例，将忽略外部荷载变化对渗流场影响的非饱和非稳定渗流计算所得不同时刻的孔隙水压力应用于稳定分析模块进行稳定分析得出的计算结果作为非耦合工况，比较耦合与非耦合两种情况下孔隙水压力分布规律的差异.

图6为上述两种情况下相同滑动面上的孔隙水压力分布情况（横坐标对应计算模型的x轴），用非饱和土流固耦合计算出的孔隙水压力比忽略应力场变化对渗流影响的非饱和非稳定渗流计算所得的结果较小，且更加符合实际，这与文献［9］中得出的结论是相似的.这是因为水位降落过程是一个卸载过程，上游坝体土体孔隙体积在一定程度上有所膨胀，从而在一定程度上减小了孔隙水压力.

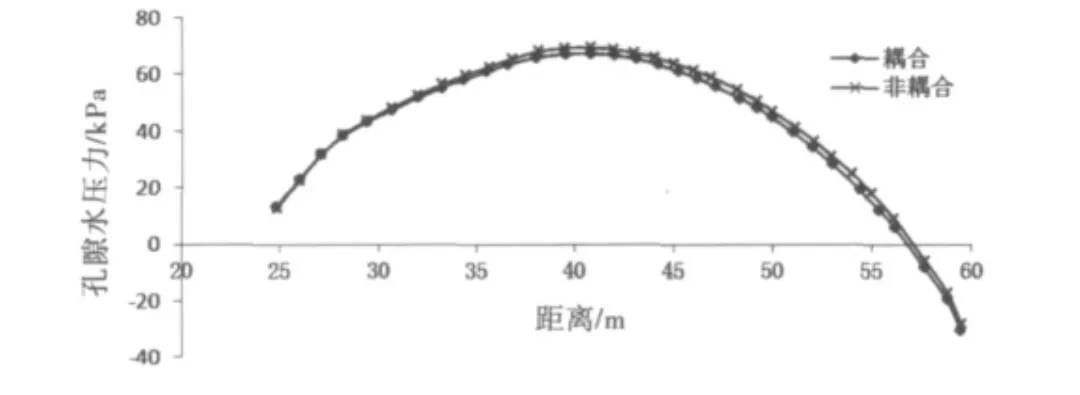
图6 滑动面孔隙水压力分布

4）本次有限元极限平衡法与传统极限平衡法的结果对比

为了说明该方法计算结果的准确性，以工况1并考虑基质吸力影响为例，分别采用Morgentern－Price法、Bishop法、Spencer法、Janbu法和Ordinary法对其进行了坝坡稳定性分析.极限平衡法计算所采用的不同时刻孔隙水压力大小同样由非饱和土耦合计算得到，各种方法计算出的稳定系数见表3.

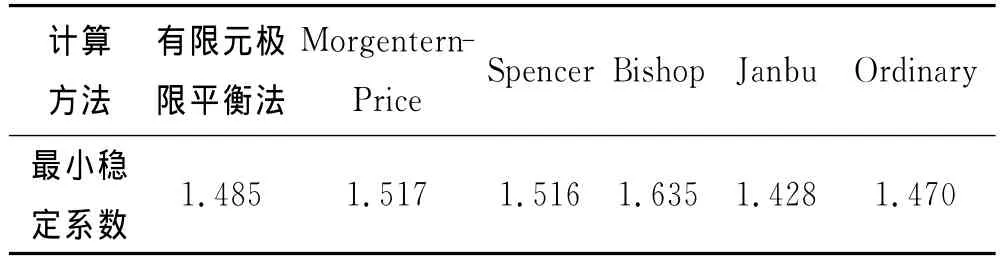
表3 计算结果对比

有限元极限平衡法计算出的最小稳定系数为1.485，虽与Bishop法计算出的最小稳定系数相差较大，为10.1%，但与理论相对严谨的极限平衡计算公式Morgentern－Price法、Spencer法计算的稳定系数都比较接近，相对误差在2.2%之内，说明了基于非饱和土流固耦合理论的有限元极限平衡法在计算水位降落下的坝坡稳定是合理可行的.

5）材料参数对坝坡稳定性的影响分析

本文采用基于 Mohr－Coulomb屈服准则的理想弹塑性土体本构模型，以工况1为例分析研究理想弹塑性本构模型中主要材料参数（弹性模量、泊松比、粘聚力和内摩擦角）对坝坡稳定性的影响.

从图7分析可知，基于非饱和土固结理论的有限元极限平衡法中，在所取的参数变化范围内，稳定系数与材料参数呈线性变化.弹性模量对稳定系数几乎无影响，稳定系数随着泊松比的增加而增加，但影响程度较小，而粘聚力和内摩擦角对稳定系数的影响较大，最大影响值在7%～15%之间.

图7 材料参数与稳定系数的关系曲线

3 结 论

基于非饱和土流固耦合理论和有限元极限平衡法原理，对某水库在水位降落过程中上游坝坡的稳定性进行了分析研究，得出以下结论：

1）采用基于非饱和土流固耦合理论的有限元法分析简单均质坝水位降落过程中坝坡的稳定性是合理可行的，其计算得出孔隙水压力分布和稳定稳定系数更符合实际情况，具有较好的推广前景.因本文仅对材料简单的均质坝进行了分析，对于坝体材料分区多、地基条件复杂的土石坝，使用该方法进行稳定分析时，其结果的合理性有待进一步研究.

2）基于非饱和土固结理论的有限元极限平衡法中，材料的粘聚力和内摩擦角对坝坡稳定系数的影响最大，泊松比影响相对较小，弹性模量几乎无影响，实际工程应根据实验获得准确而合理的计算参数.

3）基质吸力对坝坡稳定性的影响程度与坝体中非饱和区域的大小有关，当初始状态坝体内饱和区域较大，降落过程中坝体内形成的非饱和区域又相对较小，此时基质吸力对坝坡稳定的影响相对较小，是否考虑基质吸力对坝坡稳定的影响可根据实际工程在水位降落过程中坝体内非饱和区域的大小而定.

4）对于渗透系数较小的均质坝，上游水位快速降落时坝体中的孔隙水往往来不及消散而形成逆流现象，这将大大降低上游坝坡的抗滑稳定性甚至会出现滑坡，水位降落越快越不利于稳定，所以在大坝运行管理过程中要合理调度，控制上游水位下降速度.

［1］ 陈祖煜.土质边坡稳定分析——原理、方法和程序［M］.北京：中国水利水电出版社，2003.

［2］ 谢定义，姚仰平，党发宁.高等土力学［M］.北京：高等教育出版社，2007.

［3］ 贾苍琴，黄茂松，王贵和.非饱和非稳定渗流作用下土坡稳定分析的强度折减有限元方［J］.岩石力学与工程学报，2007，26（6）：1290－1296.

［4］ 周贵云，李同春.基于非饱和土固结理论的有限元强度折减法［J］.岩土力学，2008，29（4）：1133－1137.

［5］ 曾亚武，田伟明.边坡稳定性分析的有限元法与极限平衡法的结合［J］.岩石力学与工程学报，2005，24（增2）：5355－5359.

［6］ 王学武，许尚杰，党发宁，等.水位骤降时的非饱和坝坡稳定分析［J］.岩土力学，2010：31（9）：2760－2764.

［7］ GEO－SLOPE International Ltd.Stress－Deformation Modeling with SIGMA／W 2007［M］.Canada：GEOSLOPE International Ltd，March，2008：183－192，338－339.

［8］ GEO－SLOPE International Ltd.SIGMA／W Example file：Rapid Drawdown［EB／OL］.Http：／／www.geoslope.com，2012－5－16.