平行双关节坐标测量机的精度设计*

夏桂锁，费业泰 ，赵继亮

(1.合肥工业大学仪器科学与技术博士后科研流动站，合肥 230009；2.九江精密测试技术研究所，江西九江 332000)

坐标测量机作为一种近30年发展起来的高效率的新型精密测量仪器，广泛地应用于机床、机械制造和电子工业等制造业中［1］。随着科技和制造业的发展，工程实践中越来越迫切需要一种测量空间更加开阔、灵活、可移动的非正交坐标系测量系统［2］。

平行双关节坐标测量机是介于传统三坐标和关节臂式柔性坐标测量机之间的新型坐标测量机［3］。随着人们对坐标测量机的误差分析、误差补偿技术的研究深入，非正交坐标测量机的测量精度得到了显著提高，因此在要求有较高精度的便携式测量方面，平行双关节坐标测量机将扮演重要的角色。

精度设计是坐标测量机研制的基础和核心［4］，因此本文根据平行双关节坐标测量机的测量原理与结构形式分析仪器的误差来源，对仪器的误差分布做了研究，实现了仪器的误差分配，完成了精度设计研究。本文的研究为指导平行双关节坐标测量机的结构设计和标定提供了依据，为实现平行双关节坐标测量机的测量精度指标提供了扎实的理论基础。

1 测量原理和仪器结构

平行双关节坐标测量机可以实现圆柱形的测量空间，在此测量空间内，可以任意移动测头进行测量，灵活方便。且可以通过把仪器底座固定在移动小车上，实现现场测量。该测量机结构具有结构简单，体积小，重量轻，造价低等优点［5］。

如图1所示，平行双关节坐标测量机为RRP结构，R代表旋转关节，P代表直线关节，整体仪器的机构图如下图所示，本测量机主要由以下几部分组成:1为旋转关节Ⅰ、2为大连接板、3为旋转关节Ⅱ、4为小连接板、5为直线关节，测量机通过旋转关节Ⅰ与底座相连，将仪器进行固定。

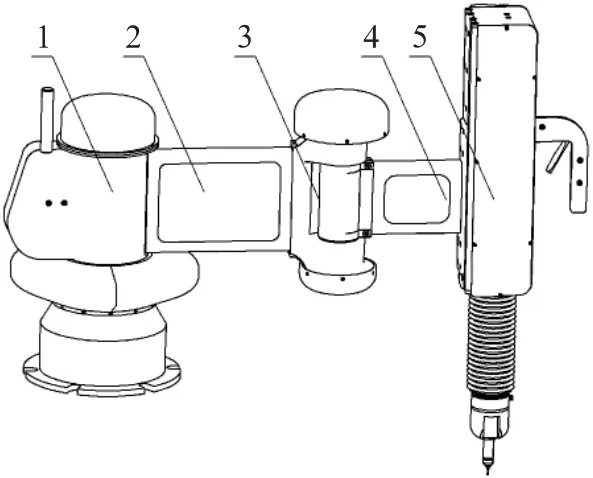
图1 平行双关节坐标测量机结构简图

2 结构参数及误差源分析

平行双关节坐标测量机测头中心的坐标误差Δp主要由各杆件的结构参数误差(Δli，Δαi，Δdi)、关节变量误差Δθi和附加误差Δβi所决定。Δθi为平行双关节坐标测量机的零位误差和测角误差；Δli，Δαi，Δdi分别为相邻两连杆旋转轴线的空间距离误差，相邻两杆旋转轴线的角度误差，和相邻两连杆的偏置误差［6－7］。为了准确的表示出这些误差对测量结果的影响，需要考察由这些误差引起的测量误差的误差模型。

假设这些误差足够小，则平行双关节坐标测量机的数学模型取全微分可得:

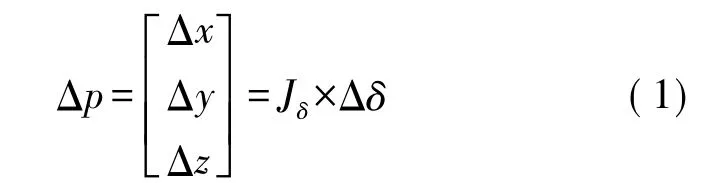
这里:Jδ是一个3×19的误差系数矩阵，即:

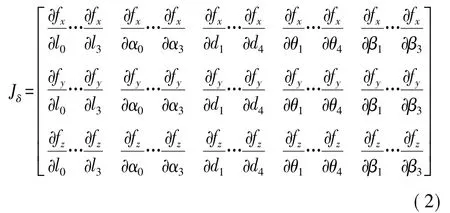
Δδ是一个19×1的误差参数矢量，是该坐标测量机的结构参数误差［8－9］，即:

平行双关节坐标测量机的测量精度取决于结构参数误差、变形误差、温度误差、其它误差等因素的综合作用，必须全面分析这些误差来源。

如图2所示，Y轴的设定符合右手定则。根据仪器结构特点，在仪器精度设计中，选取了误差最大点进行精度分析，即大、小连接板共线，直线关节行程最大处。

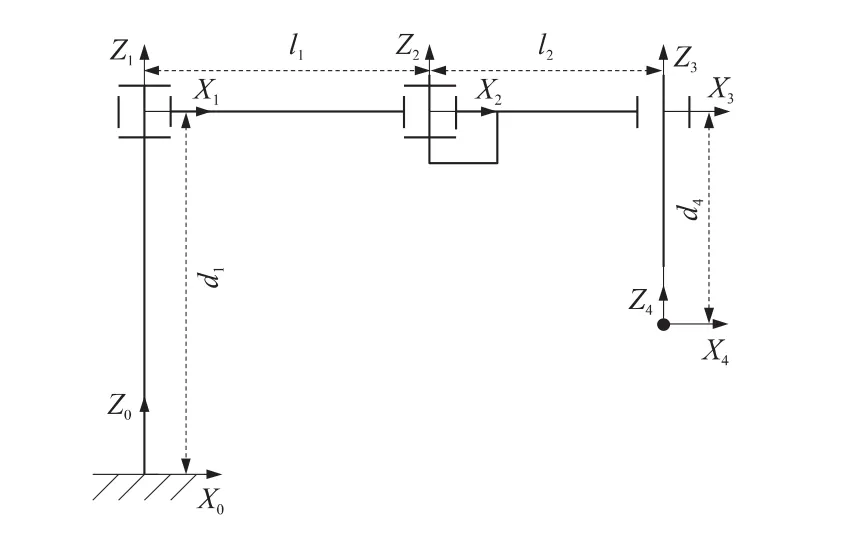
图2 平行双关节坐标测量机坐标系的建立

(1)杆件长度误差Δl1、Δl2

Δl1为旋转轴Ⅰ和旋转轴Ⅱ之间的距离误差，Δl2为旋转轴Ⅱ与测头运动直线之间的距离误差。根据实际加工装配能力，未经修正的杆件长度误差为±0.1 mm。

(2)第一关节角度误差Δθ2

圆光栅测角误差是平行双关节坐标测量机较大误差的来源，是精度控制的重点。在每一个旋转轴系中都会存在以下五类误差影响:①轴系回转误差，包括端面跳动与径向跳动；②光栅刻线误差；③读数头偏心误差；④电路处理误差；⑤零位误差。根据仪器结构设计，修正后测角误差为±1.5″，传递系数500×sinΔθ2，在该仪器状态位置，只在Y轴方向产生影响，在其它轴方向产生的影响为二次误差，可忽略，下同。

(3)第二关节角度误差Δθ3

同上，该误差由上述五项误差组成，修正后测角误差为±3.5″，传递系数 200×sinΔθ3，只在Y轴方向产生影响，其它轴方向产生的影响可忽略。

(4)直线光栅测量误差Δd4

直线光栅测量误差主要由以下四部分组成:①光栅刻线误差；②读数头偏心误差；③电路处理误差；④零位误差。该误差项是长度量，对于最终精度影响的传递系数为1，只在Z轴方向产生影响。根据所选择的器件，直线光栅误差为±0.003 mm。

(5)轴系平行度误差 Δα2、Δα3

只要系统中存在多个轴系，就会存在轴系间相对姿态的问题。根据仪器结构，此误差包括旋转轴Ⅰ与旋转轴Ⅱ的平行度误差Δα2及旋转轴Ⅱ与直线关节的平行度误差Δα3，在X轴及Y轴方向产生影响。根据实际加工装配能力，未经修正的轴系平行度误差可达到±0.25 mm。

(6)受力变形误差Δχ

平行双关节坐标测量机为悬臂结构，必然存在偏心力，使仪器产生变形，为了协调仪器刚度需求与便携性的矛盾，仪器设计为弱刚性系统，由于轴Ⅱ在旋转过程中会使轴I及大连接板受到扭转力，因此仪器在测量过程中产生受力弯曲变形及扭转变形。利用Matlab模型仪器变形情况，仪器受力变形最大位置为l1、l2处于一条直线上，d4绝对值最大处；利用有限元分析优化仪器结构设计，未补偿的仪器受力变形误差为±0.1 mm。

(7)测头重复性误差Δκ

平行双关节测量机为接触式测量仪器，测头与物体表面的接触力将直接影响到测量精度，因此该仪器选择触发测头作为测量元件，根据市场上器件的技术指标，测头重复性误差在X、Y、Z三轴方向都会产生影响，其误差为±0.001 mm。

(8)导轨平行度误差Δλ

从市场上购买的直线导轨，其自身都会存在平行度的误差，在X轴、Y轴方向产生影响。根据行程及现有高精度产品的技术指标，其误差小于±0.003 mm。

(9)温度变化产生的变形误差Δτ

对高精密测量仪器，温度误差是一个不能忽视的误差源，光栅、测量臂、导轨等器件都存在一定的热变形误差，在X、Y、Z三轴方向都会产生影响。根据仪器的特点及精度设计规划，每变化±1℃测量值变化不大于±0.01 mm。

(10)运动误差

旋转轴Ⅰ，旋转轴Ⅱ，直线关节等三部分，每一个在运动过程中都包括6个误差，即三个角运动，三个直线运动，他们中随机误差占大部分，不容易进行补偿，需要在机械制造中保证精度。

(11)其它误差Δx

预留其它误差，包括软件误差、动态测量误差及其它未知误差，分配额度为±0.005 mm，在X、Y、Z三个轴方向都会产生影响。

3 精度设计

根据上一节给出的误差源，前六项为结构参数误差，根据实际加工、装配能力估计仪器总体误差，可以得出仪器在没有进行误差修正情况下，仪器的极限误差为(误差项前面乘数决定于误差在几个轴方向产生影响):

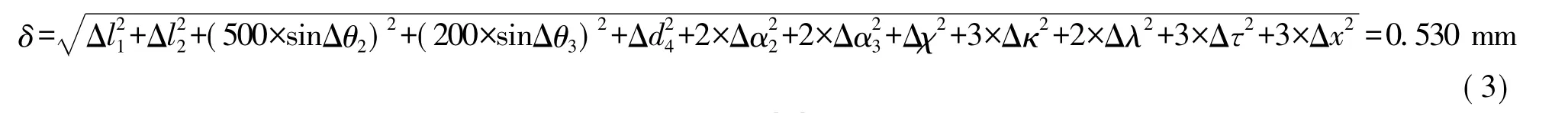
根据该仪器技术指标:空间任意距离测量不确定度［10］(K=2):12 μm；

则空间任意距离合成不确定度:6 μm。

在精度设计阶段，可将合成不确定度的计算按B类标准不确定度进行，且假定为均匀分布。

根据误差分配理论按原始误差等效作用原则对仪器进行误差分配［11－12］，并按照可能性及经济性进行调整，最终确定仪器的精度分配如下，下面所列的误差为检测时必须保证的各个误差项的精度水平。

(1)杆件长度误差 Δl1、Δl2=±0.002 mm；

(2)第一关节角度误差 Δθ2=±1.5″；

(3)第二关节角度误差 Δθ3=±3.5″；

(4)直线光栅测量误差 Δd4=±0.003 mm；

(5)轴系平行度误差 Δα2、Δα3=±0.002 mm；

(6)受力变形误差 Δχ=±0.002 mm；

(7)测头重复性误差 Δκ=±0.001 mm；

(8)导轨平行度误差 Δλ=±0.003 mm；

(9)温度变化误差 Δτ=±0.001 mm；

(10)其它误差 Δx=±0.002 mm。

则误差修正后仪器极限误差为:

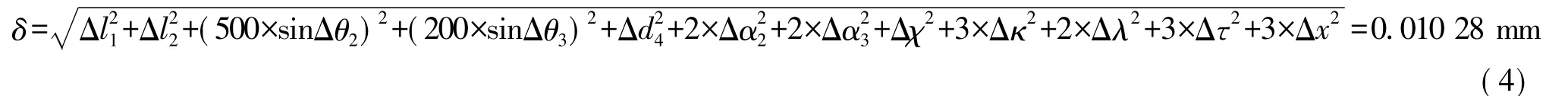
根据前一节的误差源分析计算各个轴误差:在X轴方向产生误差δ1=0.005 92 mm；在Y轴方向产生误差δ2=0.007 19 mm；在Z轴方向产生误差δ3=0.004 36 mm。从三个轴的误差分解能够看出，仪器误差在三个轴的分配较为平均，仪器总误差满足设计要求。

4 误差分布

前面计算了仪器的极限误差，下面验证仪器误差分布情况。根据式(4)，各个误差项的取值为按均匀分布的随机变量。Rand(1，1)的作用是产生(0，1)间均匀分布的随机数。则式(4)变为:

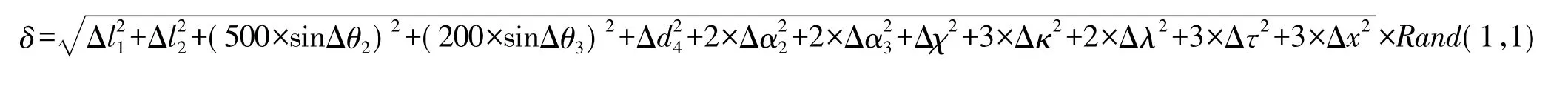
图3所示为任意取20 000点计算所得的仪器误差值，实际在仿真过程中进行了20次计算，每次取值为20 000点，每次计算所得的误差分布情况基本相同。

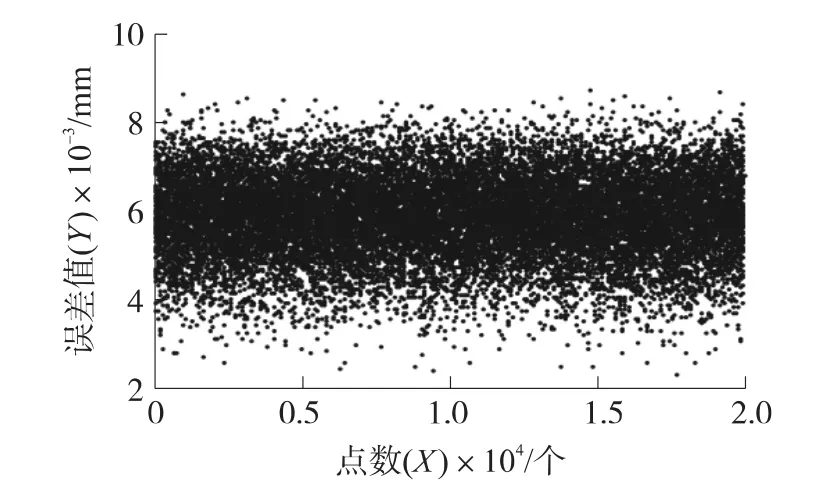
图3 仪器误差值分布1

图4所示为误差值的分布，从图中可以看出，误差的分布大致是以0.006 mm为中心的正态分布。

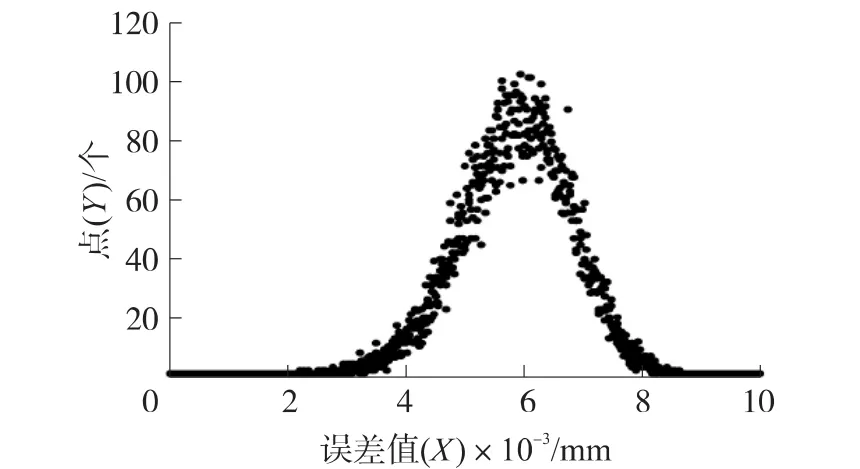
图4 仪器误差值分布2

从误差分布图上能够看出，在随机情况下，仪器的极限误差大多分布在0.006 mm附近，极限值出现的概率较小，说明仪器测量过程中的各项误差具有相互制约的作用，同时也说明了本文精度设计的合理性。

5 结论

本文从理论上全面地分析了平行双关节坐标测量机的误差来源，对测量机进行了合理的精度设计，提出了各项误差的修正精度需求，根据误差分配计算了仪器极限误差值，分析了误差分布情况，说明了精度设计的合理性。本文的研究为指导平行双关节坐标测量机的结构设计和精度分析提供了依据，为实现平行双关节坐标测量机的测量精度指标提供了扎实的理论基础。本文的研究成果可用于指导其它精密仪器的精度设计研究。

［1］Denavit J，Hartenberg R.A Kinematic Rotation for Lower Pair Mechanism Based on Matrices［J］.ASME Journal of Applied Mechanics，1995，22(6):215－221.

［2］WEI Lin，WANG Cong-jun.Coordinate Transformation and Parametric Calibration of Multi-Joint Articulated Coordinate Measuring Machine［J］.Opto-Electronic Engineering，2007，34(5):57－61.

［3］张滋黎，邾继贵，耿娜，等.双经纬仪三维坐标测量系统设计［J］.传感技术学报，2010，23(5):660－664.

［4］Monsarrat B，Gosselin C M.Workspace Analysis and Optimal Design of a 3-Leg 6-DOF Parallel Platform Mechanism［J］.IEEE Transactions on Robotics and Automation，2003，19(6):954－966.

［5］付中正，叶东，张之江，等.新型关节式三坐标测量机的研究［J］.工具技术，1997，31(1):38－40.

［6］Erik L J Bohez，Bancha Ariyajunya，Chanin Sinlapeecheewa，et al.Systematic Geometric Rigid Body Error Identification of 5-Axis Milling Machines［J］.Computer-Aided Design，2007，39(4):229－244.

［7］黄风山，岳彦芳.光笔式视觉传感技术中控制点坐标测量值的修正［J］.传感技术学报，2007，20(11):2513－2516.

［8］程文涛，于连栋，费业泰，等.平行双关节坐标测量机建模［J］.应用科学学报，2009，27(4):430－434.

［9］叶东，黄庆成，车仁生.多关节坐标测量机的误差模型［J］.光学精密工程，1999，2(7):92－95.

［10］王学影，刘书桂，王斌，等.关节臂式柔性三坐标测量系统的数学模型及误差分析［J］.纳米技术与精密工程，2005，3(4):262－266.

［11］王琦，陈晓怀，杨洪涛，等.纳米三坐标测量机的精度设计［J］.工具技术，2006，40(7):71－73.

［12］罗焱，楚纪生，王宝超，等.三关节坐标测量机测量空间分析和随机误差分布的计算方法［J］.机电产品开发与创新，2011，24(3):124－126.