梯形变截面悬臂梁式微质量传感器设计与分析*

高仁璟，赵 剑

(大连理工大学，工业装备与结构分析国家重点实验室，汽车工程学院，辽宁大连 116024)

压电式微质量传感器主要通过测量由微小质量引起的结构谐振频率变化量来检测物质成分，具有体积小、反应灵敏及自激励和自感应的特点，在细菌和病毒等微生物检测、微小颗粒探测、气/液体成分和浓度测量等方面具有广泛的应用前景。由于待测物的质量变化极其微小，传感器必须具有很高的灵敏度才能满足高精度的测量要求。悬臂梁式微质量传感器的灵敏度与结构的谐振频率成正比，探测区的质量吸附面积、结构刚度和质量等都是影响传感器灵敏度的关键因素。对于等截面悬臂梁式微质量传感器，其谐振频率与结构尺寸相关，尺寸越小谐振频率越高，传感器的灵敏度越高。因此，利用先进的工艺技术以制备更加微小尺度的传感器成为提高传感器灵敏度的重要手段［1－5］。近年来随着微纳米制造技术、电子技术及生物技术的发展，国内外研究人员围绕提高微质量传感器灵敏度的设计方法开展了大量研究工作，主要包括:(1)利用MEMS和NEMS加工技术，采用缩小传感器尺度的方法来提升传感器灵敏度［6－8］，灵敏度可以达到 10－18g 量级的吸附质量;(2)采用高弹性材料获得高灵敏度，Johansson and Butt［9］等人采用环氧聚合物制作的悬臂梁比硅悬臂梁更有弹性，且长度可以比硅悬臂梁短40倍;(3)改变各部分结构比例参数，即长度比、宽度比等参数来获得高灵敏度［10－16］;(4)利用悬臂梁结构的高阶谐振频率进行微小质量的探测［17－19］。另外，传感阵列技术［20］也为微质量传感器的发展提供了新的检测手段，实现多种不同性质的微小被测物同时测量。

虽然传感器关键几何尺寸微纳米化可以有效的提升传感器的灵敏度，但其所带来的难以在液体环境工作、动态模式不稳定、易受外界干扰及高精度测量困难等问题直接影响了其应用范围［21－22］。因此，在一定几何尺度约束下，综合考虑传感器结构尺寸、测量难易程度和实用性之间关系的高灵敏度微质量传感器的设计已逐渐引起研究人员的广泛关注。

微质量传感器在测量过程中被测物的种类存在多样性，包括液体浓度值、微小颗粒、细胞以及细菌和病毒等。液体浓度测量所需要的单位面积质量灵敏度不同，具有集中质量的微小颗粒的测量则需要单点或多点位置处的灵敏度最高。因此如何通过结构设计提升悬臂梁结构传感器在某集中区域内的测量灵敏度已成为该类型传感器设计的关键所在。文献［23］中给出的具有三角形表面的悬臂梁传感器，虽然在其尖端部位能够达到最高灵敏度，但在实际应用中被测物难以稳定放置于三角形的尖端部位，从而直接影响了其实用性。因此，针对具有集中质量的被测物的高精度测量问题，本文提出一种兼顾实用性和高灵敏度要求的变截面梁结构的微质量传感器，通过悬臂梁固定端和自由悬臂端宽度的优化设计实现高灵敏度的微小质量测量。

传感器的结构如图1所示，由等厚度(t1)的梯形变截面(变宽度)压电层、等厚度(t2)的变截面(变宽度)弹性层和固定端组成。压电层可黏贴在弹性层的单面(单压电变截面梁)或双面(双压电变截面梁)，并且具有相同的宽度。压电片覆盖弹性层的部分区域，使整体结构沿长度分解成由压电层和弹性层组成的复合段和弹性层构成的延伸段。复合段和延伸段的长度分别为l1和l2，传感器的总长度为l。传感器的宽度由固定端和悬臂端的宽度w0和w1确定。

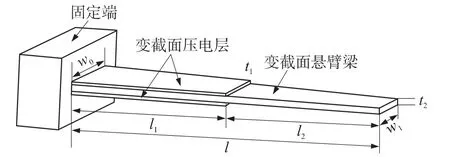
图1 双压电片变截面悬臂梁式微质量传感器的结构

1 变截面悬臂梁微质量传感器灵敏度分析

本文提出的变截面微质量传感器可简化为由变截面复合段和变截面延伸段组成的变截面悬臂梁，其振动方程可由伯努利－欧拉梁理论表示为:

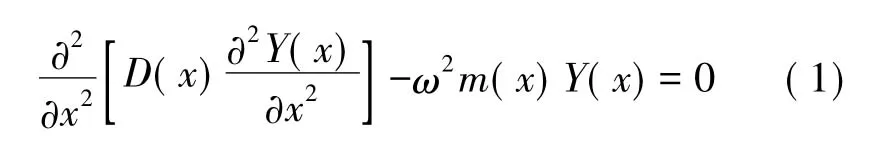
式中D(x)和m(x)分别为悬臂梁的抗弯刚度和单位梁长(线密度)的质量，在复合段与延伸段分别为不同的值。ω为自振频率，Y(x)为振幅。

按照图1所描述的变截面梁，以固定端为坐标原点，梁的截面性质参数可由位置坐标表示为:

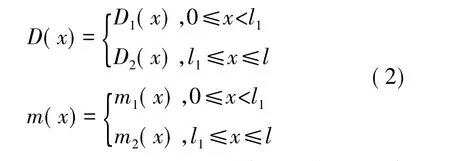
其中，D2(x)和m2(x)为弹性层延伸段的截面抗弯刚度和质量线密度，可表示为:

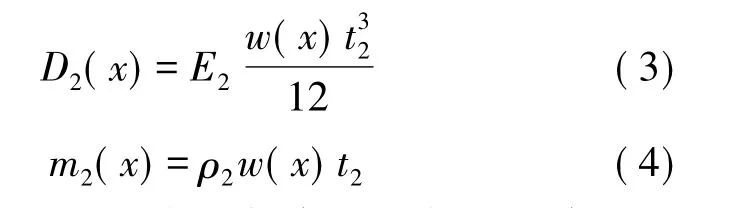
D1(x)和m1(x)为多层复合段的截面抗弯刚度和质量线密度。对于双压电层复合段其定义为:

其中，E1、ρ1为压电材料的杨氏模量和质量密度，E2、ρ2为弹性层材料的杨氏模量和质量密度;w(x)为轴向位置x处的截面宽度，可由梁的两个端部宽度表示为:

将式(3)～式(6)代入方程(1)所得到的方程为变系数微分方程，难以获得其解析解。因此，本文采用有限元法求解。

微分方程式(1)的等效积分弱形式可表示为:

其中Uad为可能的位移集合，定义为:

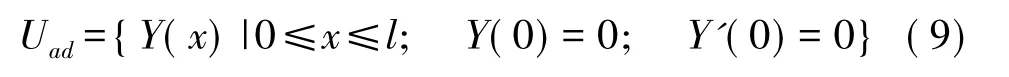
根据有限元理论，将悬臂梁沿轴向分割成n个单元，如图2所示。在每个单元内部截面的挠度(振幅值)可由该单元的两个端面的振幅通过插值函数插值获得。例如，在第e个单元内截面的振幅为:

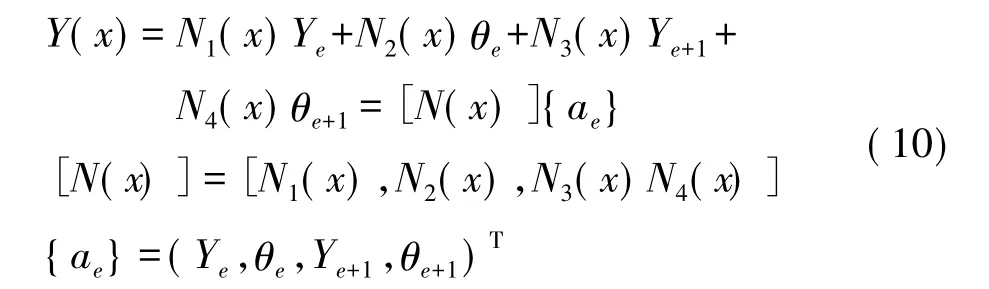
将式(10)代入式(8)得到用单元截面位移表示的振动方程:

令

［Ke］，［Me］分别称为单元刚度矩阵和质量刚度矩阵。定义整体截面位移向量{a}、总体质量矩阵［M］和总体刚度矩阵［K］，其中总体质量矩阵和刚度矩阵按照有限元方法的思想由单元质量矩阵和单元刚度矩阵组装而成。整体位移向量为:

振动方程(12)可写成以下形式的特征方程:

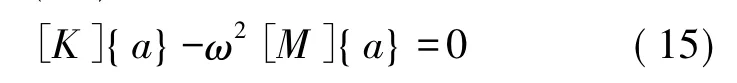
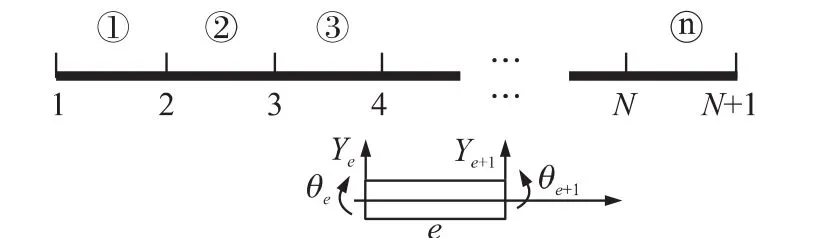
图2 传感器结构的有限元网格与典型梁单元

当梯形变截面悬臂梁传感器用于探测微小颗粒状被测物时，传感器的灵敏度可以通过单位集中质量引起的谐振频率变化量来表示:

其中Δm为被测物质量，Δfn为被测物Δm引起的第n阶频率变化量，fn为第n阶频率，为等效质量，Yn为第n阶振型。等效质量可表示为:

为了便于与文献［12］中所提出的单层压电矩形截面悬臂梁微质量传感器对比，本文采用变截面梁的参数如表1所示，数值模拟得到传感器的灵敏度如图3所示。

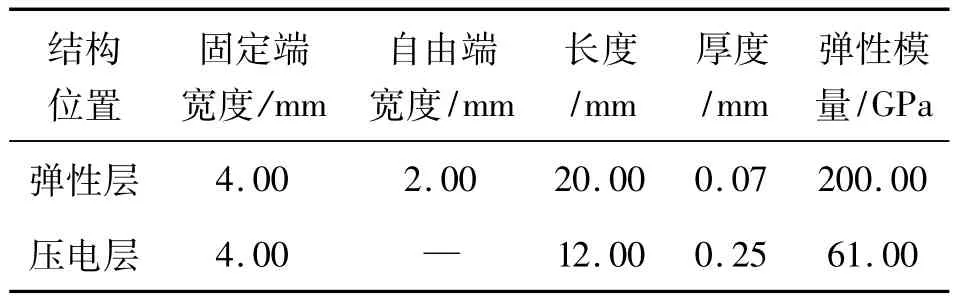
表1 变截面悬臂梁传感器参数

图3 不同结构形式传感器灵敏度对比

从图3中可以看出，文献［12］中传感器的灵敏度为48.00 kHz/g，单压电层梯形变截面悬臂梁式微质量传感器的灵敏度为109.00 kHz/g，双层压电梯形悬臂梁传感器的灵敏度为174.60 kHz/g，与文献［12］相比，灵敏度分别提高了127.00%和263.00%。因此，通过改变弹性悬臂梁和压电层的结构形式可以显著的提高传感器的灵敏度。

2 实验验证

为了验证本文提出的采用梯形变截面悬臂梁结构替代传统的矩形悬臂梁结构来提高传感器灵敏度方法的有效性，采用线切割工艺制作了单压电层梯形变截面悬臂梁传感器，如图4所示，弹性梁为高弹簧钢薄片，压电层为PZT－5。考虑到原材料及制造误差的限制，悬臂梁结构的几何尺寸如表2所示。

图4 梯形变截面悬臂梁传感器

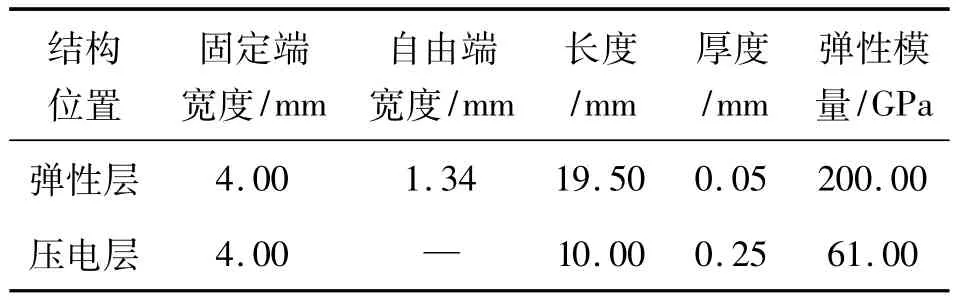
表2 变截面悬臂梁传感器参数

实验中利用WK6500B阻抗分析仪搭建微质量传感器的测试平台，利用细长导线将压电层的两个电极连接于阻抗分析仪的输入端进行频率扫描测试，测试系统如图5所示。按照表2的给定参数，理论计算得到传感器的一阶谐振频率为531.00 Hz，二阶频率为1 761.00 Hz。分析表2中传感器的结构参数发现，由于压电层与弹性梁结构具有较大的厚度比，测量过程中在满足悬臂梁结构复合段与延伸段振动连续性条件的情况下更容易激发得到二阶谐振频率。图6为单压电层梯形悬臂梁传感器的二阶谐振频率测量曲线。测量结果显示，传感器的基频为1 785.00 Hz，如图6(a)所示，红线为阻抗变化曲线，蓝线为相角变化曲线。当附加800 μg质量时，传感器的谐振频率为1 706.00 Hz，如图6(b)所示，传感器的灵敏度为98.00 kHz/g。理论仿真得到单压电层梯形悬臂梁传感器灵敏度为102.00 kHz/g，与实际测量值偏差为4.70%。造成二阶谐振频率下仿真结果与实验结果存在偏差的原因在于导电银浆涂覆厚度以及连接导线的焊点自重等使得传感器的灵敏度测量值偏低。

本文同样测试了具有相同压电层结构参数、厚度，且宽度为4.00 mm的矩形悬臂梁传感器的二阶频率灵敏度，测得其二阶谐振频率为1 540.00 Hz，对应的灵敏度为78.00 kHz/g。由此可以看出，利用梯形悬臂梁结构可以有效的提高传感器的灵敏度。

通过实验结果分析发现，采用梯形变截面悬臂梁结构可以有效地提高传感器的灵敏度，提高约25.00%。通过调整梯形变截面梁的变化斜率可以改变传感器灵敏度的提高程度。因此，可以通过截面变化率的优化设计，来优化传感器的结构形式，以获得最高的灵敏度。综合分析偏差的产生原因，本实验结果与理论仿真结果基本一致，最大偏差不超过5.00%，有效验证了本文所提出的梯形变截面悬臂梁式微质量传感器设计方法的有效性和可行性。

图5 谐振频率测试系统

图6 梯形变截面悬臂梁传感器测试结果

3 结论

本文利于变截面梯形悬臂梁结构作为传感器的关键弹性元件，提出了一种针对具有集中质量特性的被测物测量问题的高灵敏度微质量传感器的设计方法，建立了梯形变截面梁传感器的振动分析模型，采用有限元方法分析了变截面梁微质量传感器灵敏度。实验和仿真结果表明，与等截面矩形悬臂梁式传感器对比，变截面梯形悬臂梁式传感器的灵敏度获得了显著的提高。与现有的传感器灵敏度提升方法相比，本文提供了一种提高微质量传感器灵敏度的新思路，为满足特定环境需求下微质量传感器的设计提供理论依据。

［1］Lee J H，Hwanga K S，Park J，et al.Immunoassay of Prostate-Specific Antigen(PSA)Using ResonantFrequency Shiftof Piezoelectric Nanomechanical Microcantilever［J］.Biosensors and Bioelectronics，2005，20(10):2157－2162.

［2］Yi J W，Shih W Y，Mutharasan R，et al.In Situ Cell Detection Using Piezoelectric Lead Zirconate Titanate-Stainless Steel Cantilevers［J］.Appl.Phys.，2003，93(1):619－625.

［3］章安良，朱大中.Y型表面波质量传感器［J］.传感技术学报，2003，16(4):457－4611.

［4］Li P，Li X.A Single-Sided Micromachined Piezoresistive SiO2 Cantilever Sensor for Ultra-Sensitive Detection ofGaseous Chemicals［J］.Journal of Micromechanical and Microengineering，2006，16(12):2539－2546.

［5］Yang J L，Ono T，Esashi M.Mechanical Behavior of Ultrathin Micro-Cantilever［J］.Sensors and Actuators，2000，82(1):102－107.

［6］Butt H J.A Sensitive Method to Measure Changes in the Surface Stress of Solids［J］.Journal of Colloid and Interface Science，1996，180(1):251－260.

［7］Bouropoulos N，Kouzoudis D，Grimes C A.The Real-Time，in Situ Monitoring of Calcium Oxalate and Brushite Precipitation Using Magnetoelastic Sensors［J］.Sens.Act.B，2005，109(2):227－232.

［8］Li S，Y Li，Huiqin Chen，et al.Direct Detection of Salmonella Typhimurium on Fresh Produce Using Phage-Based Magnetoelastic Biosensors［J］.Biosensors and Bioelectronics，2010，26(4):1313－1319.

［9］Blagoi G，Boisen A，Johansson A.Polymeric Cantilever-Based Biosensors with Integrated Readout［J］.Applied Physics letters，2006，17:1899－2010.

［10］Yi J W，Shih W Y，Shih W H.Effect of Length，Width，and Mode on the Mass Detection Sensitivity of Piezoelectric Unimorph Cantilevers［J］.Appl.Phys.，2002，91(3):1680－1686.

［11］Shen Z，Shih W Y，Shih W H.Flexural Vibrations and Resonance of Piezoelectric Cantilevers with a Nonpiezoelectric Extension［J］.IEEE Trans.Ultrason.Ferro.Freq.Control，2007，54(10):2001－2010.

［12］Shen Z，Shih W Y，Shih W H.Mass Detection Sensitivity of Piezoelectric Cantilevers with a Nonpiezoelectric Extension［J］.Rev.Sci.Instrum.，2006，77(6):065101.

［13］熊娟，顾豪爽，吴雯，等.基于倾斜AlN薄膜的体声波质量传感器的制备及性能分析［J］.传感技术学报，2009，22(8):1114－1116.

［14］Campbell G A，Mutharasan R.Detection and Quantification of Proteins Using Self-Excited PZT-Glass Millimeter-Sized Cantilever［J］.Biosensors and Bioelectronics，2005，21，597－607.

［15］Gossett A Campbell，Raj Mutharasan.Sensing of Liquid Level at Micron Resolution Using Self-Excited Millimeter-Sized PZT-Cantilever［J］.Sensors and Actuators A:Physical，2005，122(2):326－334.

［16］Rijal K，Mutharasan R.Piezoelectric-Excited Millimeter-Sized Cantilever Sensors Detect Density Differences of a Few Micrograms/mL in Liquid Medium［J］.Sensors and Actuators，B:Chemical，2007，124(1):237－244.

［17］Maraldo D，Mutharasan R.Mass-Change Sensitivity of High Order Mode of Piezoelectric-Excited Millimeter-Sized Cantilever(PEMC)Sensors:Theory and Experiments［J］.Sensors and Actuators B:Chemical，2010，(2):731－739.

［18］Parkin J D，Hahner G.Mass Determination and Sensitivity Based on Resonance Frequency Changes of the Higher Flexural Modes of Cantilever Sensors［J］.Review of Scientific Instruments，2011，82，035108.

［19］Lochon F，Dufour I，Rebiere D.An Alternative Solution to Improve Senstivity of Resonant Microcantilever Chemical Sensors:Comparison between Using High-Order Modes and Reducing Dimensions［J］.Sens.Actuators B Chem.，2005，108:979－985.

［20］Campbell，Gossett A，Raj Mutharasan.Detection of Pathogen Escherichia Coli O157:H7 Using Self-Excited PZT-Glass Microcantilevers［J］.Biosensors and Bioelectronics，2005，21:462－473.

［21］Baselt D R，Lee G U，Colton R J.Biosensor Based on Force Microscope Technology［J］.Journal of Science ＆ Technology B:Microelectronics and Nanometer Structures，1996，14:789－793.

［22］Sader J E.Frequency Response of Cantilever Beams Immersed Invicous Fluids with Applications to the Atomic Force Microscrope［J］.Journal of Applied Physics，1998，(1):64－76.

［23］Sukuabol S，Sood D K，Rosengarten G.Geometric Optimisation of SU-8 Piezoresistive Cantilever Sensors for Biochemical Applications［C］//Proceedings of the 2005 International Conference on Intelligent Sensors，Sensor Networks and Information Processing Conference.5－8:247－252.