抗滑桩桩间土拱效应离心模型试验研究
2012-10-20中铁十七局集团第一工程有限公司李熙颖
中铁十七局集团 第一工程有限公司 李熙颖
抗滑桩桩间土拱效应离心模型试验研究
中铁十七局集团 第一工程有限公司 李熙颖
就当前来看,人们对抗滑桩自身强度的设计和处理已经形成了一套完整的理论,但对桩间距的合理选择却没有一套成熟的方法,大多是凭经验来确定。但如果桩间距过小,势必会增加成本;桩间距过大,则很可能不会产生土拱效应,易使桩间土体滑动,导致建筑损坏。因此,在设计抗滑桩时,桩间距是必须慎重决定的一个重要参数。本文,笔者通过FLAC3D软件,对砂土中的桩间距进行离心模型分析,以研究不同间距情况下的桩间土拱稳定性。这不仅对抗滑桩的设计具有一定的理论意义,而且对工程实践也有较大的指导作用。
一、实例分析
利用FLAC3D软件,对桩间净距分别为5d,6d和7d的桩体进行分析(d为桩体直径),得出的桩体弯矩曲线及不同桩间距下的弯矩对比如图1 ~ 4所示。
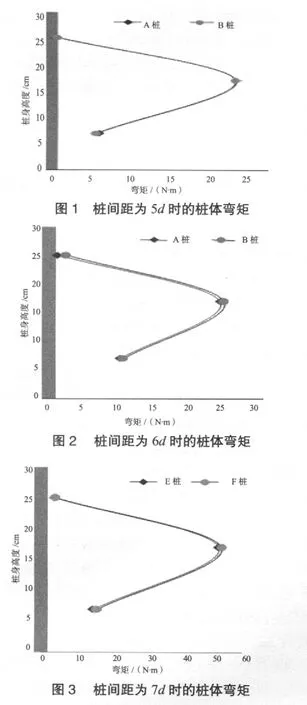
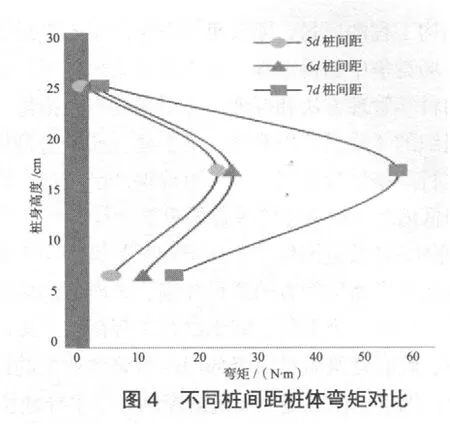
由图1 ~ 4可知,桩间距为5d时,桩间土形成连拱,且土拱矢高较小,桩间土体有开裂趋势;桩间距为6d,7d时,桩间土流出,土拱矢高急剧增大;桩体弯矩随桩身高度呈抛物线形分布;当桩间距增大时,桩体弯矩也随之增大。
从以上分析可知,抗滑桩桩间距越大,拱的受力值就越接近梁的受力值,就越难以产生土拱作用;抗滑桩桩间距越小,土拱的受力值就越能体现受压的实际情况,对土拱结构的受力就越有正面意义。总之,桩间距越大,土拱效应就相应越弱。
二、 对抗滑桩合理桩间距的探讨
从理论上来讲,滑坡工程的土拱问题是一个空间问题。这就导致难以给其建立模型,再加上力系的复杂性,因而建立模型就更是难上加难。本文,笔者将这个问题简化为有一定夹角的平面土拱问题来研究。
1.由矢高确定合理间距。在均布荷载作用下,可以假定拱的合理拱轴线呈抛物线形。这个合理拱轴线的每一个截面上只存在压力,不存在弯矩和拉力。
在此次试验中,当桩间距为n倍桩径时,可建立如图5所示的坐标系。

假定土拱中轴d 线抛物线方程如下:

当 y=f时,x= 0 ,则

当 y = 0时,x =(n-0.5)d/2 ,则

将式(2)、式(3)代入式(1),可得土拱中轴线方程为:
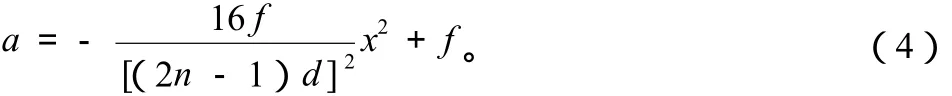
从式(4)可知,土拱中轴线方程由n , f 确定。若能建立函数 f (n) ,就可由n , f 直接确定土拱抛物线方程。假定函数f (n) 为一元二次方程,即

从试验数据可知,n=5时 ,f=1.5 cm;n=6时 ,f =1.7 cm;n=7时 ,f =3.1 cm。将以上数据代入式(5),求解得函数 f (n)的一元二次方程

方程两边对n求导,可得

当 f '= 0时,n= 5.3, f 有最小值,即桩间距为5.3倍桩径时,土拱矢高最小,为最佳桩间距。
将式(6)代入式(4),可得土拱中轴线方程
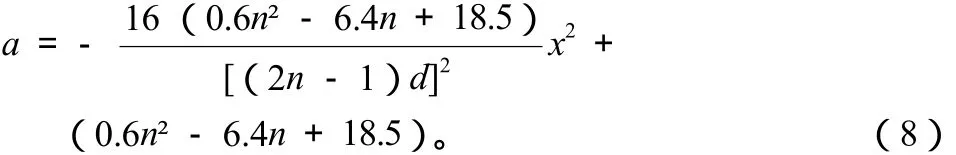
2.由弯矩确定合理桩间距。可假定桩体弯矩与桩间距的变化曲线函数M(n)为一元二次方程,即

由试验所得的测点最大弯矩值可知,n=5时,M= 23.43 N·m;n = 6时,M= 25.78 N·m;n=7 时,M= 53.51 N·m,将以上数据代入式(9),可得a=12.7 N/m,b=-137.36 N/m ,c=393 N·m。将 a,b ,c 的值代入(9),可得函数M(n)的一元二次方程为:
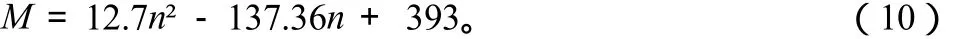
方程两边对n求导,可得

当 M '=0时,n=5.4 ,M 有最小值,即桩间距为5.4倍桩径时,弯矩值最小,为最佳桩间距。
三、结论
1.桩间距与土拱矢高关系分析。桩间距较小时,土拱矢高较大,土拱受力呈现受压特征,容易形成稳定的土拱,土体不致从桩间滑出。桩间距较大时,土拱曲线形状趋于平缓,土拱矢高较小,土拱的受力趋于梁的受力,难以形成稳定的土拱效应;或者说土拱效应随桩间距的增大而减弱。
2.最佳桩间距的确定在一定条件下的砂土中,抗滑桩的最佳桩间距为5.2 ~ 5.5倍桩直径。桩间距过大,就无法起到拦阻作用;桩间距过小,则工程造价较高。只有保持合理的桩间距,才能在保证工程结构的同时,获得较高的经济效益。
