基于循环前缀的OFDM同步算法研究
2012-10-20杨国庆
杨国庆,苏 凤
(烟台南山学院计算机与电气自动化学院,山东烟台 265713)
0 引言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统作为多载波系统无法通过分析眼图找到最佳采样时刻,定时偏差较单载波系统更为敏感。定时估计不准确就可能引起严重的码间干扰,并且载波频率偏差估计是在定时估计后进行的,定时估计的不准确,也会引起频偏估计不准确,从而破坏子载波之间的正交性,引起严重的载波间干扰[1,2]。定时估计方法主要分2类:一类是在 OFDM帧中加入训练序列来实现,这类算法精度较高,但一定程度上降低了数据传输效率。另一类使用OFDM符号本身的循环前缀来实现,不需额外数据,适用于DAB、DVB等数据帧循环前缀较长的系统[3]。主要研究了基于循环前缀的定时同步算法,并在最大似然估计算法的基础上提出了改进算法并进行了仿真。
1 OFDM系统
OFDM的基本思想是将高速数据流串并转换为N路速率较低的子数据流,用它们分别去调制N路频率正交的子载波后再并行传输。子数据流的速率是串并转换前的1/N,即符号周期扩大了N倍,远大于信道的最大延时,这样就把一个宽带频率选择性信道划分成N个窄带平坦衰落信道,使系统的抗多径衰落、脉冲干扰的能力增强并具有较高的频谱利用率。
OFDM符号包含多个经相移键控(PSK)或正交幅度调制(QAM)的子载波。如果N表示子载波个数,L表示循环前缀的长度,dn(n=0,1,2,…,N-1)是分配给每个子信道的数据符号,则OFDM符号可表示为:

接收端采样的数据可表示为:

式中,h(n)为多径衰落信道模型,φ为载波相位偏移因子,ε为归一化载波频率偏差,n(k)为零均值的加性高斯白噪声采样。
2 ML定时估计算法
Van de Beek J J提出的基于循环前缀的最大似然估计算法(Maximum Likelihood,ML)[4]是符号定时估计的经典算法。OFDM符号循环前缀的L个样本点和符号最后L个样本点在干扰不大的情况下具有较强的相关性:样本在循环前缀内,与其相隔N个样本点的样本是一致的,两者具有很好的相关性;不在循环前缀内时,两样本是相互独立的。ML算法如图1所示。

图1 ML算法示意图
设发射信号s(k)子载波个数为N,循环前缀长度为L。接收端信号存在2个不确定性:OFDM符号的开始时刻θ和接收端与发射端的相对频差ε。接收端的基带数字信号可表示为:
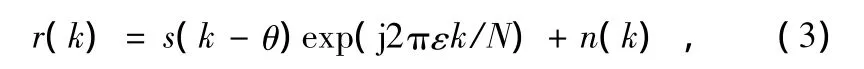
式中,n(k)为高斯噪声的采样。
由图1可知一个OFDM符号有N+L个采样点,连续2N+L个样本必包含一个完整的OFDM符号。假定OFDM符号起始位置为θ。定义2个集合I、I’:

式中,I是第i个OFDM符号的循环前缀,与OFDM符号中I’的元素相同。将2N+L个样本点作为一向量:

相关关系如式(5):
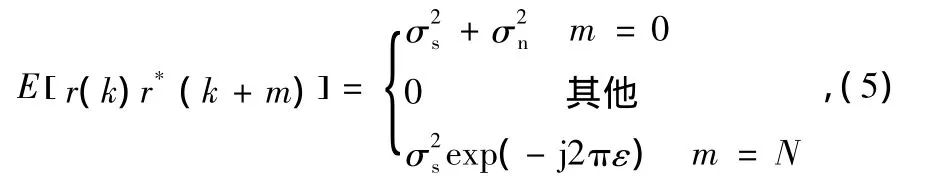
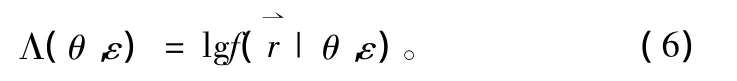
[4]推导可得最大似然函数:

算法在高斯信道下性能较好,通过相关运算得到尖锐的相关峰;但在多径衰落信道环境下由于循环前缀受到符号间干扰(ISI)的影响使得相关性减弱,得到的符号起始位置摆动较大,定时估计性能下降[5]。
3 基于整体相关的改进算法
针对ML算法在多径衰落信道环境下定时估计性能下降的问题,Karthik等人提出了一种基于整体相关的定时估计算法(Ensemble Correlation,EC)[6]。该算法可检测多径时延带来的影响并实现定时估计。多径环境下,循环前缀一部分受到符号间干扰,通过长度为L的相关窗滑动获得相关值,其中有一部分是具有相关性的,而另一部分则由于多径带来的符号间干扰的影响使得相关性减弱。EC算法采用总体相关来进行相关检测:检测多个OFDM符号循环前缀的数据与其复制的序列中数据的相关性。观察窗口由ML算法的2N+L个采样点变为M(M>2)个OFDM符号,滑动窗口由L个采样点变为N+L个采样点,算法如图2所示。

图2 EC算法原理图
对接收序列 r(k),定义一个相关值 C(k),C(k)=r(k)r*(k+N)即序列的第1个数据与间隔N个采样点的数据进行相关处理。对各个OFDM符号中相同位置上的数据与其对应的数据进行相关处理后求和。OFDM符号中相同位置的数据之间间隔为N+L个样值点,所以总体相关是取间隔为N+L个样值点的数据与其对应数据进行相关后的值,再做求和处理。
这里定义一个整体相关系数ρ(k):

因为整体相关函数逐一地检测OFDM符号持续时间内相同位置的数据经过信道传输受到的影响,能较精确地检测信道时延扩展,并得到循环前缀中没有受到符号间干扰的部分。采用EC算法可以保证定时估计能稳定地落在循环前缀区域,但同时造成相关峰存在一个较长的平坦区域(未受ISI影响的循环前缀部分),引起定时估计的不准确性并增加了检测的复杂度。
因此,在EC算法的基础上对算法进行改进:利用EC算法得到未受符号间干扰的循环前缀(CP)的长度作为有效的截短循环长度进行最大似然估计,就能避免循环前缀受ISI影响带来的相关性下降,得到准确的定时估计。定义CL=length(ISI-free CP)为未受ISI影响的CP长度。
定义△=length(CP)-length(ISI-free CP)为截短CP距离OFDM符号起始位置的距离差。对截短CP进行相关运算得到定时估计:

4 仿真实验
仿真中所用的参数为:采用QPSK调制,子载波数N=2048,循环前缀 L=64,OFDM符号长度为224 μs,单个样值点 0.1094 μs,信噪比 SNR 从 0 ~20 dB,每次递增2 dB,每个SNR仿真1000次,EC算法中M=50,采用4径衰落信道,时延分别为0、10、20、40个样值点,幅度衰落相对直达信号分别衰减0、10、20、25 dB。
通过仿真可知在高斯环境下,测度平台由于白噪声的影响出现细小的尖峰,如图3所示,但循环前缀的每个样值点都与其对应的数据保持了较好的相关性,测度平台仍然保持长度L。在多径条件下,测度平台的宽度随着信道的时延扩展而变窄,如图4所示。改进算法有效利用截短CP进行最大似然估计,提高了定时估计的准确性并减小了检测的复杂度,仿真表明改进算法在高斯信道下与ML算法性能差别不大,在多径环境下定时估计性能明显提高,如图5所示。
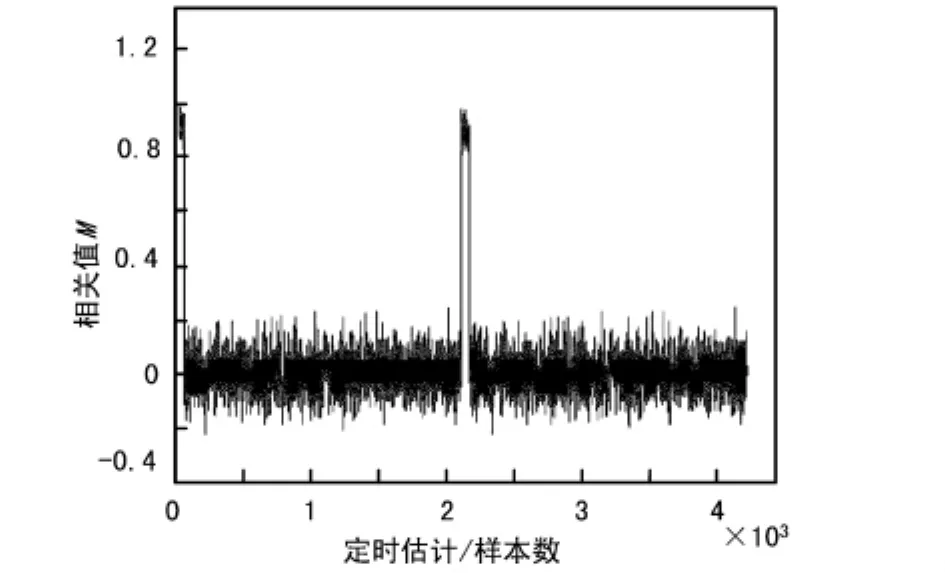
图3 EC算法在高斯信道环境下的定时估计相关峰
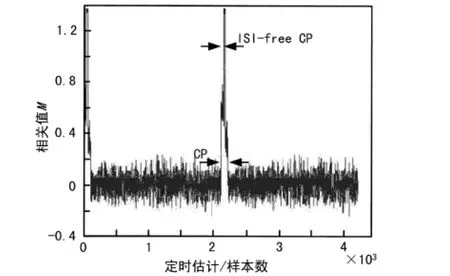
图4 EC算法在多径衰落环境下的定时估计相关峰

图5 2种定时同步算法性能仿真
5 结束语
针对OFDM信号在多径环境中码间干扰带来的定时估计误差,研究了一种基于整体相关的定时同步算法,通过扩大检测范围减小了多径衰落的影响。与传统的ML算法相比较,在高斯信道环境和多径衰落信道环境下都取得了较好的性能。
参考文献
[1]STEENDAM H, MOENECLAEY M.Sensitivity of Orthogonal Frequency Division Multiplexed Systems to Carrier and Clock Synchronization Errors[J].Signal Processing,2007,80(7):1217-1299.
[2]KELLER T,HANZO L.Adaptive Multicarrer Modulation:A Convenient Framework for Time-frequency Processing in Wireless Communications[J].Processings of the IEEE,2007,88(5):611-640.
[3]ETSI TS 101759 V1.1.1(2000.09),Digital Audio Broadcasting(DAB),European Broadcasting Union[S].
[4]BEEK J J V D,BORJESSON P O.ML Estimation of Time and Frequence Offset in OFDM Systems[J].IEEE Trans Signal Processing,1997,45(7):1800-1804.
[5]张海滨.正交频分复用的基本原理与关键技术[M].北京:国防工业出版社,2006:34-35.
[6]RAMASUBRAMANIAN K,BANUM K.An OFDM Timing Recovery Scheme with Inherent Delay-spread Estimation[C]∥New York:IEEE GLOBECOM,2001:3111-3115.
