改进的构造函数盲均衡算法研究

2012-10-20王晓东白长河

无线电通信技术 2012年6期

王晓东，白长河

(中国人民解放军92785部队，河北秦皇岛 066004)

0 引言

当前电磁环境日益复杂，军事通信信号在传输过程中会受到多径效应的严重影响，导致信号特征发生畸变。在实践中多采用均衡技术来消除多径效应的影响。由于传统的均衡器需要依赖不断地发送训练序列来调整均衡器系数，而盲均衡技术仅利用接受信号序列就可以实现信道均衡，所以盲均衡技术的研究得到了普遍的关注。常模算法(CMA)是实际中应用较为广泛的盲均衡方法，其具有收敛性能稳健，计算复杂度低的优点。但同时也有收敛速度慢，剩余误差大，存在相位偏转、不适合处理多模信号等不足。

针对CMA算法无法修正相位偏转的问题，文献［1］提出了修正常模算法(MCMA)，实验结果表明该算法有效解决了相位旋转问题，但是对收敛速度和剩余误差的改善不明显。文献［2］针对CMA算法处理多模信号不理想的情况提出了修正多模算法(MMMA算法)，分析表明该算法不仅解决了相位旋转问题，而且进一步减小了剩余误差。文献［3，4］在文献［1］的基础上进一步改进，通过构造函数的方式利用了函数的确定信息，使均衡器收敛后的剩余误差更小。由文献［5，6］可知，分数间隔均衡的性能要明显优于波特间隔，所以利用上述文献的改进思想提出了修正构造函数算法，并通过实验仿真验证其均衡性能。

1 算法描述

1.1 常用盲均衡算法介绍

设{a(n)}是原始发送序列，{h(n)}是信道冲激响应，{x(n)}是经信道加噪后的信号，{w(n)}是采用抽头延迟线模型的线性均衡器，{y(n)}是均衡后的信号，{e(n)}代表迭代误差。在CMA中误差函数定义为:

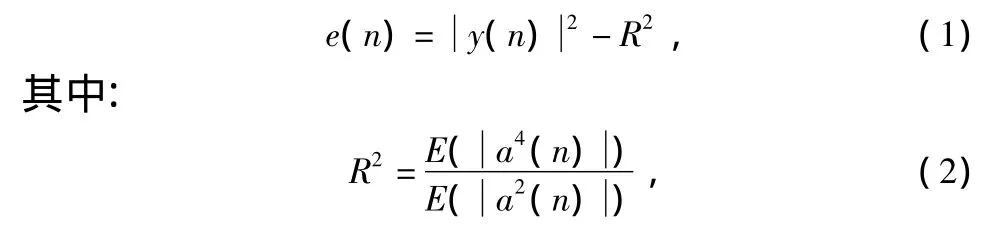
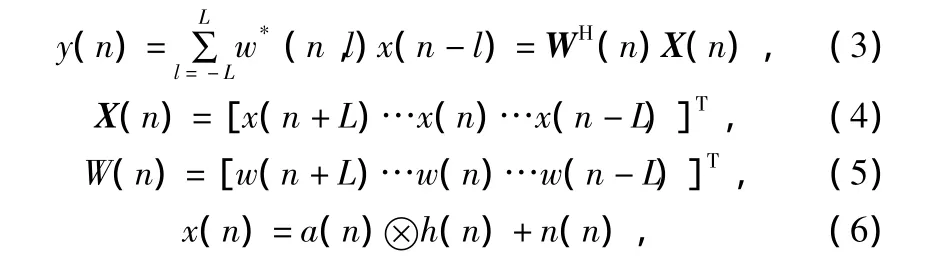
式中，T表示转置，H表示共轭转置，⊗表示卷积，*表示共轭。

在CMA算法中其代价函数为:

均衡器权向量的迭代过程为:

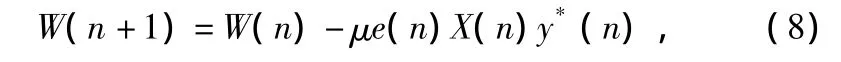
式中，μ表示步进长度。

可以看出CMA的误差函数仅包含信号的幅度信息，这样就导致不能克服信道引起的相位误差。文献［1］中提出分别对信号的实部和虚部进行均衡的MCMA算法，在均衡过程中既包含了信号的幅度信息又包含了相位信息，从而可以补偿信道引起的相位偏转。该算法误差函数的实部和虚部分别为:

CF算法就是在此基础上引入1个构造函数，以64QAM为例，对于单路信号而言在信号发生端有8个数据 -7，-5，-3，-1，1，3，5，7。对于这个 8 个数据构造 1个函数 φ(x)，满足条件:φ(x)=0，x∈(-7，-5，-3，-1，1，3，5，7)。构造这样 1 个函数的目的是使均衡器的输出也能满足上述条件，同MCMA相比，构造函数算法利用了信号的确知信息，所以在信号收敛后稳态误差会进一步减小。参考文献［3］令φ(x)=Acos(π/2x)，所以抽头函数的递推公式为:

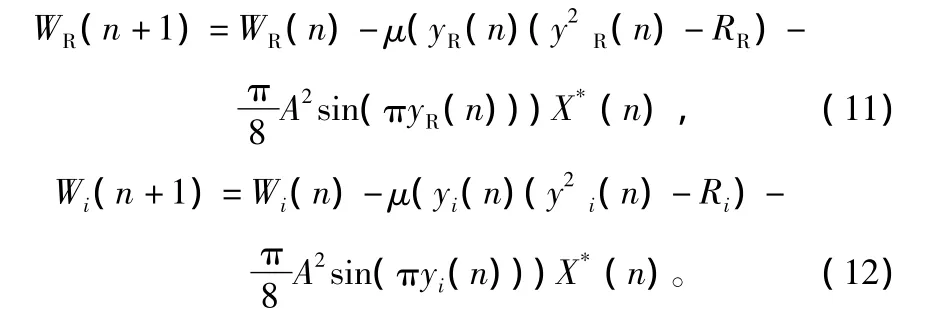
上式中的A值一方面表示了函数的幅度，另一方面也隐含了 φ(x)在(-7，-5，-3，-1，1，3，5，7)这8个点处的变化率。A愈大，这4点处的变化率就越大，函数的区分度就愈好，但A并不能太大，否则不能保证算法的收敛性。

1.2 新算法描述

由式(11)和式(12)可知，CF算法中的模值R是恒定值，这样就会导致均衡器输出的数据向半径为的圆上靠近，而QAM信号属于非常模信号，星座点分布在多个圆上，所以采用CF算法处理QAM信号在算法收敛后势必会存在剩余误差大的问题。针对此问题，对CF算法做了进一步改进，提出修正构造函数算法(MCF)，即用均衡器输出的判决值来代替CF算法中的R［4］，使均衡器输出与信号的多个模值相吻合，算法收敛后稳态误差趋于0，如此便解决了CF剩余误差大的问题。改进后的均衡器抽头函数递推公式为:

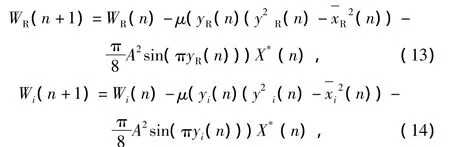
评价均衡效果的2个重要指标是收敛速度和收敛后的剩余误差大小，MCF算法相对CF算法仅减小了剩余误差，而在收敛速度方面并没有改善。上述方法都是采用波特间隔均衡器，分数间隔均衡器的采样频率大于或者等于奈奎斯特频率，从而避免了因欠采样引起的频谱混叠，均衡器可以在较低信噪比环境下补偿更严重的时延和幅度失真。所以利用分数间隔均衡器的这一优势，提出了FSE-MCF算法。与CF算法和MCF算法相比，该算法收敛速度快，稳态误差小。综合考虑均衡器的性能和复杂度，采用1/4分数间隔均衡器，该均衡器比1/6、1/8结构简单，同时又比1/2分数间隔结构收敛速度快，稳态误差小，系统框图如图1所示。

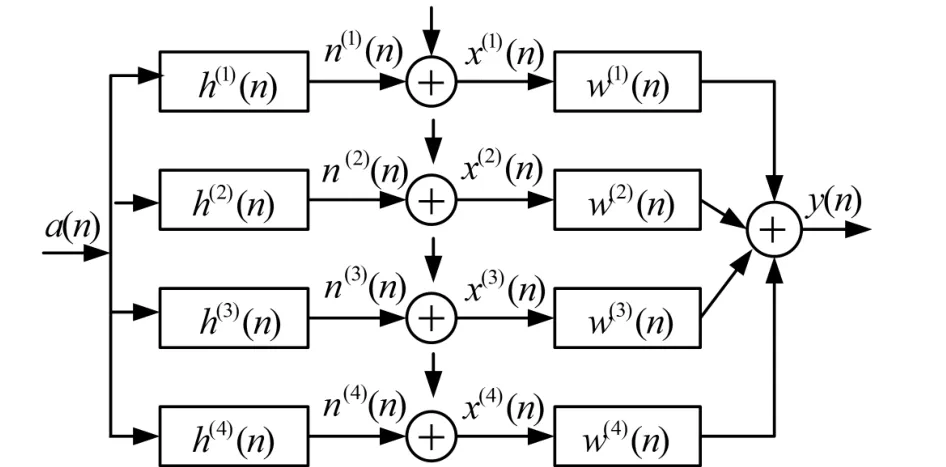
图1 1/4分数间隔均衡器系统框图

图1中{a(n)}是原始发送序列，h(i)(n)表示子信道i(i=1，2，3，4)的冲击响应，且子信道长度为L，写成向量的形式为:

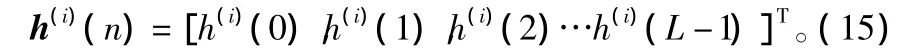
N(i)(n)表示子信道i的加性噪声，x(i)(n)表示第i个子滤波器的输入信号，w(i)(n)表示第i个子滤波器的系数，用向量表示为:

则该均衡器在采样时刻n的输出y(n)为:

2 仿真结果分析

以常用的64QAM信号作为处理信号，信道的冲击响应h=［0.9344-1.0311j 2.2483-1.6682j-1.0780-0.2138j-0.6742+0.8835j 0.3755-0.2771j 0.0886+0.0628j］，均衡器的阶数为11，步进长度为0.0002，构造函数中A=4，信噪比分别为10 dB、15 dB和20 dB，仿真结果如图2和图3所示。

图2 信号未均衡及CF算法、FSE-MCF算法均衡后星座图

图3 2种盲均衡算法剩余误差曲线图

图2中图(a)显示的是接收端数字信号在未经过均衡时的星座图，图(b)显示的是接收信号经过CF算法均衡处理后的星座图，图(c)显示的接收信号经过改进算法FSE-MCF均衡后的信号星座图。由图(a)可以看出经多径信道传输后信号星座图模糊一片，信号特征发生了严重的畸变。对比图(b)和图(c)可以看出在相同条件下，经改进的FSEMCF算法均衡后的信号星座图的收敛性要优于CF算法。图3显示的CF算法和FSE-MCF算法均衡中的剩余误差曲线图，从图中可以看出不仅FSE-MCF算法收敛速度比CF算法快，而且其剩余误差也远小于CF算法。仿真结果分析可见，改进算法在剩余误差和收敛速度方面确实得到了明显的改善，具有一定的参考意义。