Kdv－Burgers方程初边值问题的Lp－衰减估计

易菊燕，罗祠军，陈 诚

(暨南大学 数学系，广州510632)

1 引言及主要定理

考虑下列广义KDV－Burgers方程的一般初边值问题

其中:f是充分光滑的函数，u±是给定的常数.假设f是严格凸的，即存在某个正常数α使得

并且假定特征速度f'(u±)满足

对边界条件作如下假设

在全空间上考虑与式(1)相应的双曲守恒律Riemann问题

其弱熵解是一个稀疏波

当δ=0时，(1)1称为Burgers方程.关于Burgers方程的Cauchy问题和初边值问题的解收敛到稀疏波的渐近性研究已有了不少的结果[1－3].当 μ ＞0，δ∈R时，Z·A·Wang和C·J·Zhang[4]讨论了(1)1的Cauchy问题.当u-＜u+时，在小初值扰动及小强度的条件下，证明了此Cauchy问题存在惟一整体解，并且解渐近收敛到稀疏波.当μ=1，δ=-1时，文献[5]讨论了广义Kdv－Burgers方程初边值问题解的大时间性态，在对初边值做适当小性限制或使f满足某种增长条件下，运用L2-能量方法在u-＜u+的条件下得到稀疏波解的整体存在性.本文在u-＜u+，小初值扰动及小强度的条件下，研究一般初边值问题(1)的解的整体存在性及解衰减到一个稀疏波的衰减率，并由此澄清了一般边界条件对解的衰减率的影响.

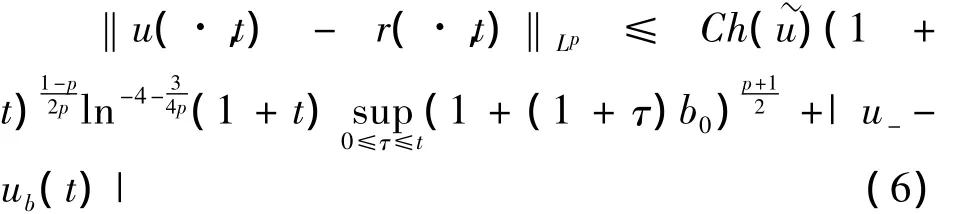
记号注释:文中用Ca，b表示仅依赖于a，b的一般正常数，或在没有混淆的情况下，简记C，Lp=Lp((0，∞))表示一般Lebesgue空间，其范数为表示一般的Sobolev空间，其范数为记表示在[0，T]上取值于的k次连续可微函数空间.为简洁起见，用‖·‖表示‖·‖L2，用‖·‖m表示‖·‖Hm.

2 整体解的渐近收敛性

首先采用Hattori和Nishihara在文献[6]中的思想来构造稀疏波的光滑逼近函数.定义为如下Cauchy问题

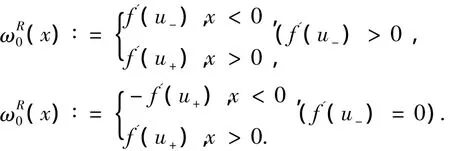
由于式(8)1为Burgers方程，利用Hopf－Cole变换能够得到的显式表达式，进而定义稀疏波r(x，t)的光滑近似 ω(x，t)为

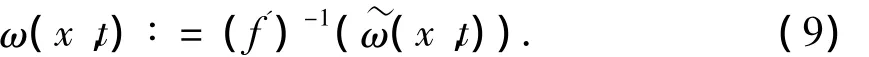
接下来，对边界进行修正，定义修正光滑逼近函数W(x，t)为

其中:Ψ(x，t)∶=(ω(0，t)-ub(t))e-x，

下面定义扰动v(x，t)∶=u(x，t)-W(x，t).则问题(1)转化为

引理2.1对于1≤p≤∞，t≥0，W(x，t)和Q(x，t)满足

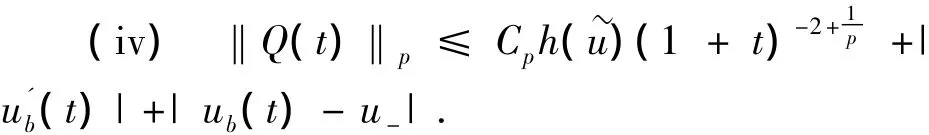
要得出问题(11)解的存在性，需要应用局部解的存在性和先验估计.

首先定义解空间

命题2.2(局部存在性)假设v0∈H1(R+)，则存在一个仅依赖于‖v0‖1≤M和‖ub(·)-u-‖H1.1的正常数T，使得问题(11)有惟一解v∈X2M(0，T).

类似文献[7]，用标准的迭代方法证明命题2.3.为了把命题2.3中得到的局部解延拓到四分之一平面，还需要得到以下先验估计.

命题2.3(先验估计)假设v(x，t)∈X2M(0，t)是问题(11)在命题2.3中得到的局部解，满足先验假设

则存在不依赖于T的正常数C，使得v(x，t)满足

证明 首先取得扰动v(x，t)的L2-估计.(11)1式两边同乘以v得

将(13)在R+上关于x积分，并由式(11)中的边界条件得

由先验假设，根据Sobolev不等式可得到‖v‖∞≤Cδ1，(14)左端第二项可由式(2)及引理2.1(iii)估计为

其中:ξ夹在W与W+v之间.

由Cauchy不等式，式(14)右端估计如下

将(17)在(0，t)上关于t积分，同时由引理2.1(ii)(iv)得

特别地，有

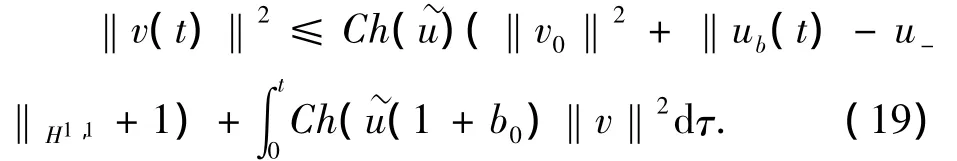
对上式应用Gronwall不等式，得到

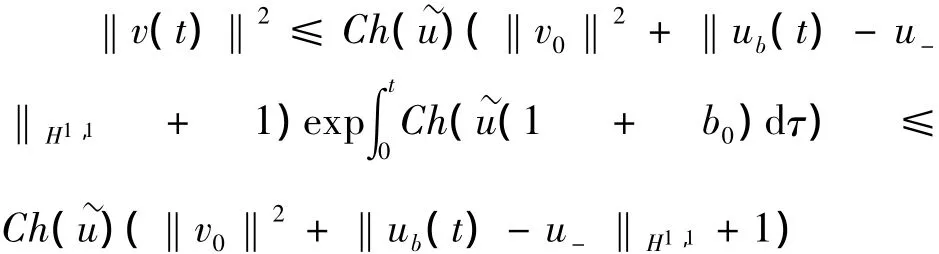
将上式代入式(18)最后一项，可得

利用Wx的有界性和以及Cauchy不等式估计式(21)左端第二项得

由Cauchy不等式，式(21)右端估计如下

将上式在(0，t)上关于t积分，同时由引理2.1(ii)(iv)及式(20)得

最后由式(20)和式(25)即得所需的估计式(12).至此命题2.3得证.

引理2.4若g(t)≥0，g∈L1(0，∞))且g'∈L1(0，∞)，那么当t→∞ 时，g(t)→0.

结合命题2.2，2.3及引理2.4可以得到以下解的整体存在性定理.

3 衰减估计

由于W(x，t)足够快地收敛到稀疏波r(x，t)，因此要证明定理1中的估计式(6)和(7)，只需导出的v(x，t)衰减估计，因此我们需要建立v的如下L1-估计.

命题3.1(L1-估计)假设，则问题(11)的解v(x，t)满足

将(11)1式两边同乘)得

计算式(27)左边的第二项和第三项，并由引理2.1(iii)得

及

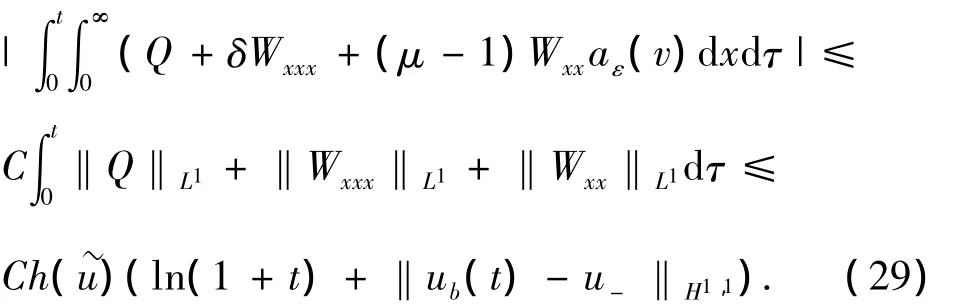
由于K1在R+上的积分等于0，K1＞0，K4＞0.对式(27)在R+×(0，t)上积分并利用以上估计式，然后令ε→0即可得到所需估计式(26).

其中:2≤p＜∞.

特别地，若取|u--ub(t)|，|u'b(t)|=O(1)(1+t)-1则有如下估计式

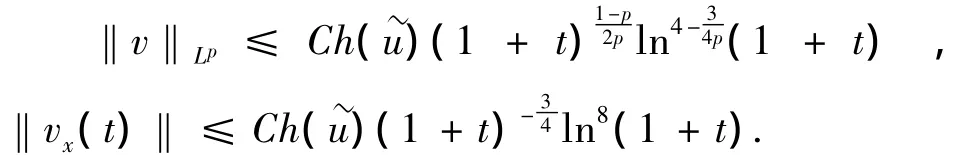
证明 首先推导关于v的收敛率估计.在方程(11)1两边同乘以|v|p-2v得

由W及Wx的有界性，式(30)左边最后一项利用(2)式及引理1(iii)可得

将式(30)右边第一项在(0，∞)上关于x积分得

当p=2时，利用分部积分可知(32)是不大于0的.由于p=2时v相应的衰减估计的证明思路与p＞2时类似，证明过程略[8-9]，因此此处仅给出其估计式

将(11)1两边同乘以-vxx，利用引理1(ii)(iv)，Cauchy不等式，Gagliardo－Nirenberg不等式，Young不等式及式(33)，可证得vx满足如下估计式

特别地，若取|u--ub(t)|，|u'b(t)|=O(1)(1+t)-1则有如下估计式

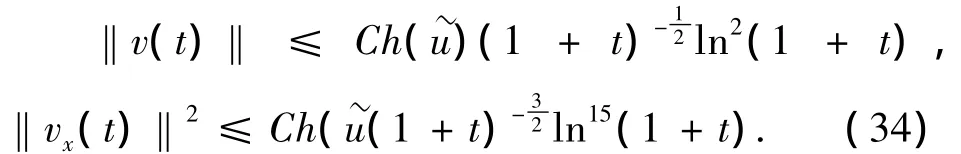
下面主要证明p＞2的情形.当p＞2时，(32)可变为

将估计式(31)和(35)代入式(30)，并在(0，∞)上关于x积分得

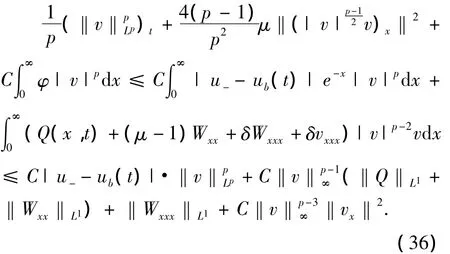
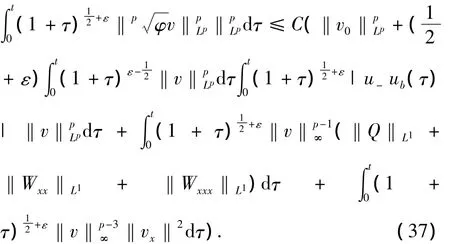
其中ε1为任意小的正常数.

最后也类似地估计式(37)右端最后一项得

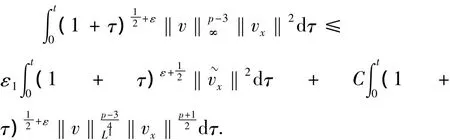
取ε1足够小，将以上估计式代入式(37)可得

利用引理1(ii)(iv)，及(34)式估计J1，J2，J3得

类似地

及

将以上估计式代入式(39)可得

定理3.2证毕.

[1]HARABETIAN E.Rarefactions and large time behavior for parabolic equations and monotone schemes[J].CMP，1988，114:527－536.

[2]IIIN A M，OLELINIKO A.Behavior of the solution of the Cauchy problem for certain quasilinear equations for unbounded increase of the time[J].AMS Transl.，1964，42(2):19－23.

[3]KAWASHIMA S，NISHIBATA S，NISHIKAWA M.Asymptotic stability of waves for two－dimensional viscous conservation laws in half space[J].Discrete and Continuous Dynamical Systerms，2003(Suppl.):469－476.

[4]WANG Z A，ZHU C J.Stability of the rarefaction wave for the generalized Kdv－Burgers equation[J].AMS，2002，22B(3):309－328.

[5]YAO L，RUAN L Z.Asymptotic stability of rarefaction waves for the generalized Kdv－Burgers equation on the half－line[J].Nonl.Anal.，2009，70(1):372－384.

[6]HATTORIY，NISHIHARA K.A note on the stability of the rarefaction wave of the Burgers equation，Japan JIAM，1991(8):85－96.

[7]SCOTT JF.The long time asymptotic of solution to the generalized Burgers equation[J].PRSL，1981，373(A):443－456.

[8]ITO K.Asymptotic decay toward the planar rarefaction waves of solutions for viscous conservation laws in several space dimensions.MMMAS，1996(6):315－338

[9]NAKAMURA T.Asymptotic decay toward the rarefaction waves of solutions for viscous conservations laws in a one–dimensional half space.SJM.Anal.，2003，34(6):1308－1317.