SCILAB在考试的能力结构和维度研究中的应用

2012-10-17曲霄红

网络安全技术与应用 2012年5期

曲霄红

山西大同大学教育科学与技术学院山西 037009

0 前言

开源科学计算自由软件SCILAB具有运行稳定，占用计算机资源少，运行速度快等优点，已经被广泛地引进到教育研究、教学及产品开发中。

教育考试的目的是根据考生在考试设计的行为目标上的测量结果，推测考生具有哪些心理结构，包括心理结构的性质和不同心理结构之间的关系。以考试语言表述，这些心理结构实质就是考试测量的能力，能力结构就是指这些能力的性质以及它们的相互关系。考试维度是指完全描述考生群体在考试中表现出的差异所要求的最小能力数。

从教育测量的角度看，命题人员希望同一试卷中部分试题测量的是某一主要潜质，另一部分试题测量另一主要潜质，即一个试卷可以分解成若干个单维量表。每个单维量表总分的意义比较明确，可以解释考生在考试中的表现依据。这就需要研究考试的能力结构和维度。

1 能力结构和维度分析的原理

从统计学角度看，我们可以利用因子分析的方法分析考试的能力结构和维度。因子分析实际上是一种统计方法，该方法分析一组观察变量与少数假设变量的关系，统计学上称这些假设变量为因子，并且认为这些因子包含了分析的观察变量的大部分信息。因子分析利用观察变量之间的相互关系，以及观察变量与因子之间的关系，用少数因子来解释观察变量的大部分信息。

设有p个观察变量，对n个考生进行测试后，获得的测量结果为xi(i=1，2，…，p)，而且测量结果已经标准化，即每个观察变量的测量结果的平均值为0，方差为1。因子模型为：

式中，Fj(j=1，2，…，m)是由标准化的观察变量分解出来的相互独立的公共因子，其平均值为 0，方差为 1，它们是不可观测的，其含义要根据具体情况来解释。Ei是各观察变量xi所特有的因子，称为特殊因子。它们与公共因子Fj相互独立，表示xi中所不能被公共因子解释的部分。aij是观察变量i在因子j上的负荷，也就是观察变量i与因子j的相关系数。

上式也可以表示成矩阵形式：

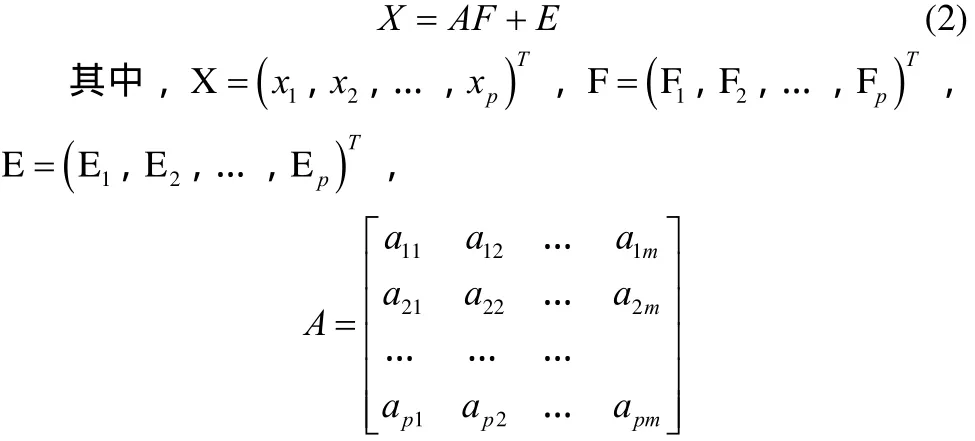
2 因子分析的步骤

2.1 确定观察变量是否合适做因子分析

因子分析是从众多的原始变量中构造出少数几个具有代表意义的因子变量。这里有一个潜在的要求，即原有变量之间要具有比较强的相关性。如果原有变量之间不存在较强的相关关系，那么就无法从中综合出能反映某些变量共同特性的少数公共因子变量来。

判断原始变量是否合适做因子分析，最简单的方法就是计算变量之间的相关系数矩阵。如果在相关系数矩阵在进行检验时，大部分相关系数都小于 0.3，那么这些变量不适合做因子分析。

2.2 构造因子变量和因子矩阵

因子分析中有多种确定因子变量的方法，获得了相关系数矩阵后，需要决定采用哪一种因子分析模型进行因子分析。总体上主成分法是最常用的确定因子变量的方法。

提取出因子后，必须确定应该保留多少个因子，也就是确定考试的维度。保留的因子数不同，对考试内部结构解释也不同，考试结果的一系列处理方式都将相应不同。因此，因子分析研究时要认真考虑应该保留多少个因子。确定保留的因子数有多种规则，这里选用的规则是：根据方差的累积贡献率来确定，通常取累积贡献率为80%。

2.3 因子旋转

提取出因子后，有时可能难以根据因子负荷对因子进行解释和命名。解决这个问题的方法就是对因子进行旋转。因子旋转可以改变因子的负荷结构，因此可以改进对因子的解释。

实际应用过程中，可以对因子分析结果进行旋转，因子旋转分为正交旋转和斜交旋转。通常最常用的因子旋转方式是正交旋转中的方差最大正交旋转。

2.4 因子含义的解释

因子分析的最主要结果是因子负荷和因子得分。这些结果一般以旋转的因子负荷矩阵和因子得分系数矩阵形式报道。

对因子进行解释实际上就是解释哪些观察变量在因子上的负荷有意义。这种意义包含两个方面，统计意义和实际意义。

实际意义就是要确定一个变量在因子上的负荷应该多大才有实际意义。如果变量在因子上的负荷为 0.2，则该因子只能解释该变量方差的4%，这个结果可能太小。J.F.Hair等建议，为了保证因子对变量方差的解释有实际意义，一般因子负荷最低应该在0.3，比较重要的变量应该在0.4以上，大于0.5才真正有实际意义。

3 SCILAB实现分析考试的能力结构和维度

3.1 因子分析算法

根据因子分析法的原理和步骤，这里描述利用因子分析法分析考试的能力结构和维度的计算过程(如图1所示)。

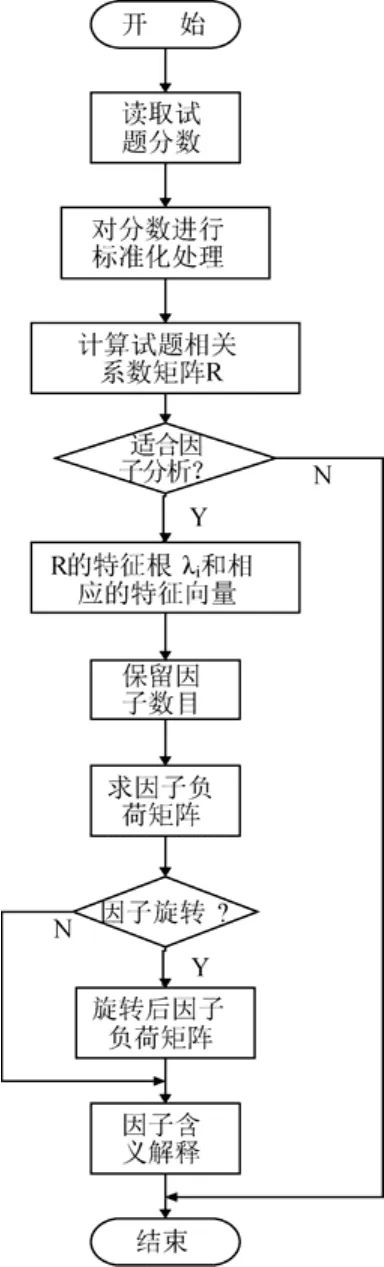
图1 因子分析流程图

3.2 分析英语考试的能力结构和维度

以 2009年贵阳市中考英语科目的部分试题分数为例，并选用试卷中的3道阅读方面的试题t1,t2,t3和4道写作方面的试题t4,t5,t6,t7的分数作为变量。在SCILAB 4.1.2 平台上编写因子分析算法，利用因子分析法确定其能力结构和维度。

表1是根据2009年贵阳市中考英语科目的部分试题成绩计算的相关系数矩阵，从中得知观察变量的测量结果是可靠的。表1可看出试题间相关系数都大于0.30。说明试题间有较好的相关性，适合进行因子分析。

从表1可以看出，有两组相关度较高的试题变量。一组是阅读试题t1，t2，t3，另一组是写作试题t4，t5，t6和t7。每一组变量都是某一潜在变量，即因子的外显变量。

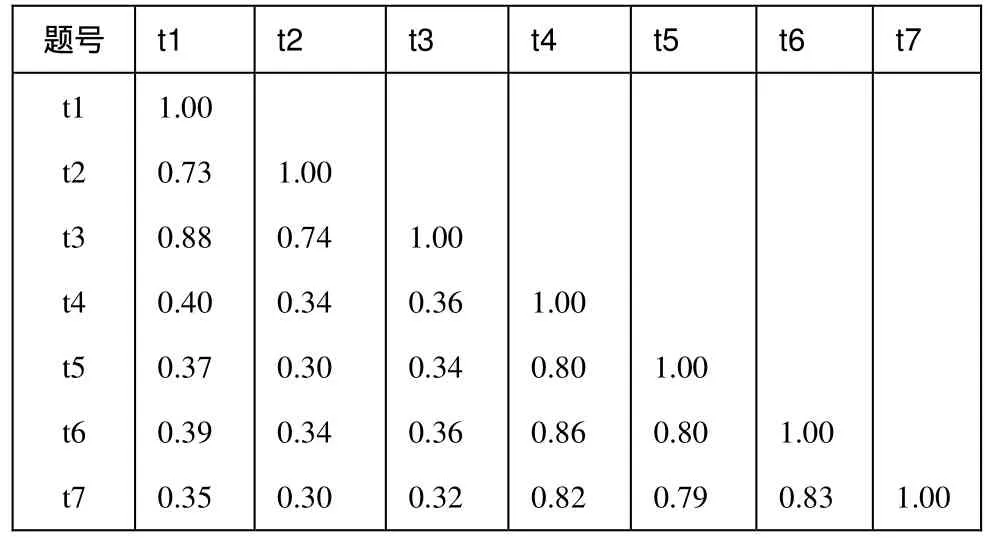
表1 试题相关系数矩阵

表2是由表1中试题相关系数求得的相关系数的特征值和特征向量表，从表2中可以看出前两个特征值的累积百分比为86.0%，结合因子保留的规则，可以提取两个公共因子，并且认为这两个因子基本反映了原变量的绝大部分信息。

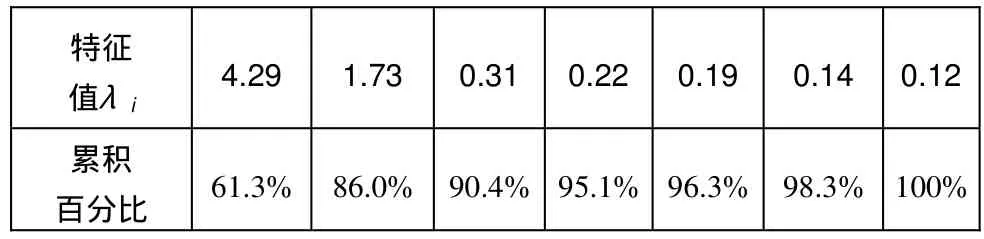
表2 相关系数矩阵的特征根和特征向量

由表3得知，绝大多数的变量共同度都在0.80以上，说明这7项指标之间存在着高度的信息重叠，既验证了数据间的高度相关性，也体现了资料数据的较高可靠性。从表3中可以看出，所有试题变量在因子1上都有相差不太大的正负荷，因子2上负荷有正有负，暂时不好解释因子变量的含义。

表3 公共因子负荷矩阵、共同度、及公共因子方差贡献

为了更加合理解释因子变量的含义，需要将表3中的初始因子负荷矩阵进行因子旋转，经过因子旋转后，三道阅读试题t1，t2，t3负荷集中在因子2上，负荷分别为0.92,0.87和0.93；最小的负荷为0.87，最大的负荷为0.93。四道写作试题在因子1上的负荷分别是0.91,0.89，0.92和0.91，介于0.89到0.92之间。因此，可以确定因子1为写作能力因子，解释为表达信息的能力；因子2为阅读能力因子，解释为接受信息的能力；确定测试是二维的。

由上述分析得出考试的能力结构同实际水平基本吻合，这两个因子的累计贡献率达 86.1%，它们基本上解释了每个试题变量的变异的绝大部分。