煤矸石推剪试验的颗粒离散元细观模拟

段 巍， 张孟喜

(1．上海大学 土木工程系，上海200072;2．上海城建市政工程(集团)有限公司，上海200065)

煤矸石推剪试验的颗粒离散元细观模拟

段 巍1，2， 张孟喜1

(1．上海大学 土木工程系，上海200072;2．上海城建市政工程(集团)有限公司，上海200065)

以现场推剪试验为基础，基于二维颗粒离散元(two dimensional particle flow code，PFC2D)建立煤矸石推剪试验模型．通过不同级配和孔隙率反映治理前后不同密实度的矸石散粒体，较好地模拟煤矸石现场推剪试验的推力-位移曲线;对比分析治理前后推剪模型推力-位移曲线的差异性，从细观力学角度验证推剪试验中矸石颗粒的运动规律．颗粒离散元模拟结果表明:治理前后推剪模型都存在接触力沿滑裂面传递的现象;由于碾压作用，治理后推剪模型的接触力呈倒月牙形分布;治理后煤矸石试样在推剪完成后，其颗粒接触力与水平方向的夹角比治理前更大，集中分布区域更狭窄．通过颗粒位移矢量图确定推剪试验的滑裂面，解决了煤矸石推剪试验中滑裂面难以确定的问题．

煤矸石;颗粒离散元;推剪试验;滑裂面

Abstract:Based on two dimensional particle flow code(PFC2D)，a horizontal push-shear test model of coal waste is established to simulate the push-shear tests that gangue have different compactness before and after improvement reflected by different gradation and porosity．The pushing force-displacement curves of the coal waste specimens are reproduced and verified by the PFC2Dmodel，and the difference in the curves is analyzed．The law of particle mobilization in push-shear tests is verified from the perspective of mesomechanics．The results show that the contact force in the model will transmit along the slip surface．Distribution of contact force after improvement presents inverted crescent-type．Furthermore，the angle between the direction of contact force and the horizontal in the model after improvement becomes larger，and the contact force concentrates in a narrower area．The slip surface is also determined in push-shear tests by means of the displacement vector chart．

Key words:coal waste;particle flow code;push-shear test;slip surface

煤矸石是采煤和洗煤过程中排出的固体废弃物，其排放量正以每年近亿吨的速度在增加，已成为我国累积堆积量和占用场地最多的工业废物．由于煤矸石往往采用露天堆积方式，煤矸石边坡时常由于稳定性问题，发生坍滑、坍塌、滑坡、泥石流等地质灾害，因此研究煤矸石山体的力学特性具有重要意义．

鉴于矸石散体力学特性的复杂性，试验是一种直接有效的研究方法和手段．刘松玉等［1］通过中型三轴试验及现场大型直剪试验得到了煤矸石强度包线的形式和参数，以及煤矸石抗剪强度、围压和孔隙比随粗颗粒含量的变化规律．贺建清等［2］通过筛分试验、击实试验、固结试验、渗透试验、承载比试验和直剪试验，深入研究了掺土对煤矸石工程力学特性的影响．由于煤矸石粒径较大、粗颗粒含量过高，任何试验条件的改变都可能引起材料强度的显著变化，因此，常规的室内试验已经不适用．臧亚军等［3］通过现场大型直剪试验、推剪试验研究了矸石山体的抗剪特性，分析了矸石山不同部位的抗剪强度特性．李晓等［4］提出并规范了针对土石混合体的原位推剪与压剪试验仪器、方法、步骤及其关键问题等．吴硕等［5］对土石混合体进行了原位压剪以及推剪试验研究，揭示了土石混合体在原位受剪情形下的变形与破坏规律，并发现了煤矸石以及碎石类土在推剪试验过程中由于需要开挖试样而容易产生扰动的现象，且存在推剪滑裂面不明显等问题．

目前国内外学者采用颗粒流分析的手段研究了土体的细观作用机理，主要以室内试验为基础．Powrie等［6］采用PFC3D模拟非圆颗粒的平面应变试验，结果表明颗粒离散元可以很好地模拟室内试验的土体宏观特性．Zhang等［7］通过离散元方法研究了加筋土的拉拔破坏机理．周健等［8］利用离散单元法中的二维颗粒流方法对福建标准砂常规三轴试验结果进行了细观数值模拟．史旦达等［9］对砂土直剪力学过程进行了非圆颗粒仿真模拟，揭示了细观组构各向异性的演化规律及其与宏观剪切强度之间的宏细观关联．杨贵等［10］通过比较粗粒料真三轴颗粒流模型试验结果和室内真三轴试验结果，发现三维颗粒流程序能够较好地模拟该种材料的三维力学特性．在现场试验的颗粒流模拟方面，贾学明等［11］基于三维颗粒离散元PFC3D，建立了土石混合料直剪试验模型，进行了不同含石量、不同岩性的土石混合料直剪试验模拟研究．严颖等［12］通过构造三维组合颗粒单元来描述颗粒间的互锁效应，对非规则颗粒材料的力学行为进行了离散元数值模拟，并通过碎石料的直剪试验进行了验证，结果表明组合颗粒单元可用于模拟非规则颗粒材料．孟云伟等［13］以工程中的实体石笼挡土墙为原型，建立了墙背阶梯式石笼挡土墙数值模拟模型，通过在填土表面施加均布荷载，研究了挡土墙的力学行为．

煤矸石是一种不连续的颗粒介质，因而研究中采用非连续的颗粒离散元［14］数值模拟技术更加合理．基于已有研究，本工作提出了一种基于PFC2D的煤矸石现场推剪试验方法，通过不同级配和孔隙率反映治理前后不同密实度的矸石散粒体，研究治理前后煤矸石散粒体内接触力的变化;分析煤矸石在推剪试验过程中的细观机理，以研究不同密实度煤矸石在推剪过程中的强度特性、颗粒接触力传递规律以及滑裂面的形成过程;并研究了推剪速率对推剪试验结果的影响．

1 建立数值模型

二维颗粒离散元PFC2D(two dimension particle flow code)，即二维颗粒流程序，是基于离散单元法，通过模拟圆形颗粒介质的运动及其相互作用来研究颗粒介质的特性．PFC2D应用于岩土工程中的散粒体介质时，通过设定散粒介质的细观力学参数，对试样颗粒单元的几何尺寸进行设计，使得颗粒间的相互作用可以用接触本构模型来代替．

1．1 推剪模型

现场推剪试验装置如图1所示，其中1为推剪土体;2为千斤顶;3为支撑板;4为加载板(尺寸为70 cm×30 cm);5为垫板．PFC2D模型中wall 4用以模拟加载板，高度为30 cm(见图2)．建立PFC2D模型时，不仅需要模拟推剪试样内的土体，还需对推剪试样下部及右侧土体进行模拟，以考虑推剪过程中试样外土体对试样的约束作用．因此，在加载板下取40 cm深度以考虑试样下部土体的作用，模型长度取为140 cm以考虑试样右侧土体的作用．PFC2D模型边界由wall 1～wall 5组成，由于现场试验过程中地基顶部没有约束，所以当颗粒在模型内循环完成后，需将wall 3删除，以解除地基顶部约束，使颗粒在自重作用下达到平衡．

1．2 煤矸石颗粒生成

煤矸石由单位厚度的圆盘颗粒模拟，煤矸石粗颗粒与细颗粒的直径相差很大，且粗颗粒的含量较多．治理前后粗颗粒的最大粒径分别为300和150 mm，最小粒径均小于0．5 mm．在建模的过程中，为模拟治理前后矸石体的力学特性，根据现场实测颗粒级配，生成颗粒时考虑两种不同的级配．考虑到细颗粒对试验结果的影响较小，并且若按煤矸石的实际最小粒径生成颗粒的话，将生成几十万个颗粒，会使得计算机运行十分缓慢，甚至可能无法运行．综合以上因素，将颗粒的最小粒径取为4 mm，将粒径在4 mm以下的颗粒都归为4～10 mm粒径范围，其他粒径范围内的颗粒含量不变，各粒径范围颗粒含量如表1所示．由于采用二维模型，孔隙率与实际三维情况不能等同，因此需要进行转换．考虑到煤矸石颗粒的不均匀性，采用Hoomans等［15］的方法将三维孔隙率转换为二维孔隙率，即

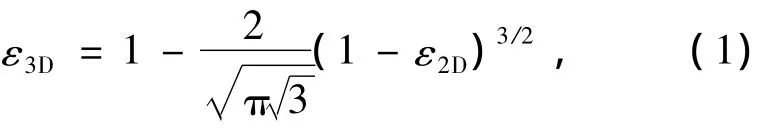
式中，ε3D，ε2D分别为三维和二维孔隙率．通过计算得出治理前推剪模型的孔隙率为0．14，治理后模型的孔隙率为0．12．生成治理前后推剪试验模型的颗粒如图3所示，其中深色网格为标识颗粒的色带．

图1 推剪试验装置结构Fig．1 Structure of push-shear test apparatus

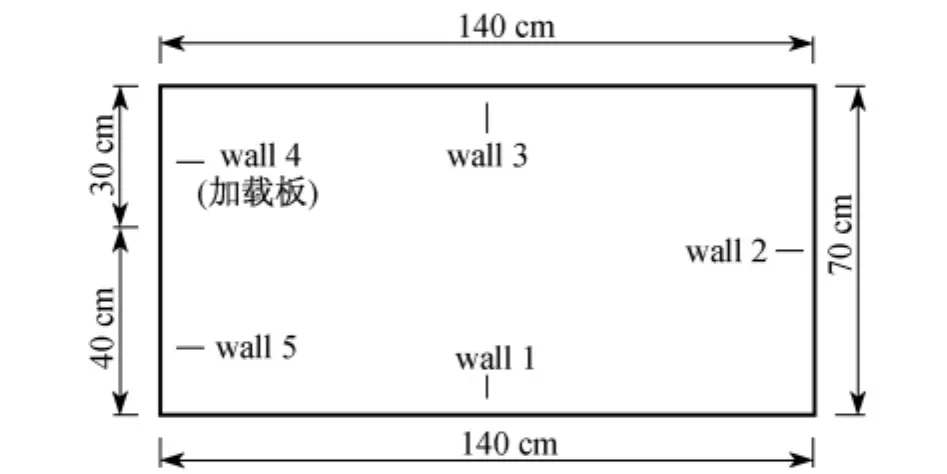
图2 PFC2D模型示意图Fig．2 Sketch of PFC2Dmodel

图3 PFC2D推剪试验模型Fig．3 PFC2Dmodel of push-shear test

表1 不同级配下颗粒组成Table 1 Particles composition with different gradation

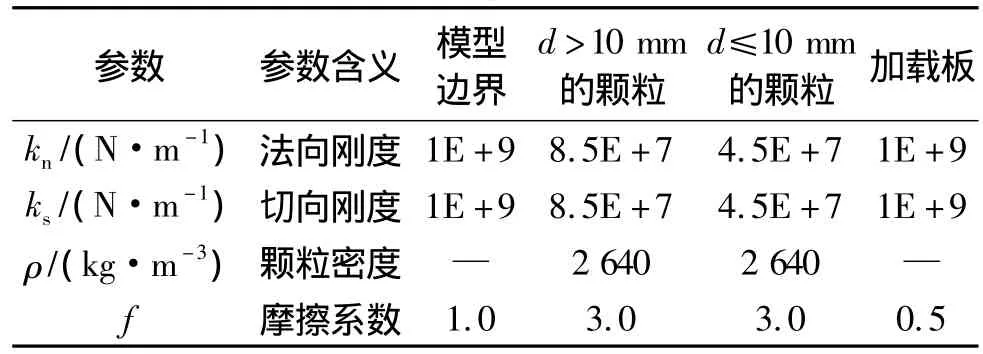
表2 PFC2D模型细观参数Table 2 Values of micro parameters in PFC2Dmodel

本次颗粒流模拟采用PFC2D内的线性接触模型，由于煤矸石颗粒之间没有粘结力，煤矸石散粒体之间主要依靠颗粒间的摩擦传递剪力，因此，本次数值模拟不需要定义颗粒间的连接强度．通过调整颗粒刚度和摩擦系数以及墙体刚度和摩擦系数，使得所模拟的推剪试验得到的推力-位移曲线和试验过程基本一致．对于墙体，不仅要保证其起到边界的作用，还要使其可以比较合理地模拟地基模型以外的煤矸石颗粒对地基模型内颗粒的影响．经过大量试算，最终确定的细观参数如表2所示．

2 数值模拟结果分析

2．1 推剪试验模拟

2．1．1 制样过程模拟

制备现场推剪试验试样时，需要采用人工开挖的方式，在开挖的过程中，试样内部的应力必然发生变化．为了真实地反应试样内部的应力分布，将wall 4以10 mm/min的速度向左移动，运行时间步长以小于程序确定的最小时间步长为准，根据试算结果，将时间步长定义为0．05 s．同时，对 wall 4水平和垂直方向所受的平均接触力进行实时监测，当2个监测值稳定为0时，认为颗粒在自重作用下达到受力平衡状态，即开挖卸压完成．试样制备完成后颗粒间的接触力分布如图4所示．

图4 试样制备完成后的接触力分布Fig．4 Contact stress distribution after specimen preparation

从图4可以看出，治理前煤矸石推剪模型由于孔隙率较大，接触力基本由颗粒的重力作用所产生，呈现从上到下接触力逐渐增大的趋势，颗粒与边界间也存在一定的接触力，并且在大颗粒分布区域接触力明显更大．经过开挖卸压后，试样的前端颗粒间接触力消散，但由于治理前颗粒对侧面墙体的挤压作用并不明显，接触力总体变化不大．而治理后推剪试样内部的接触力分布情况与治理前相比有很大差异．治理后煤矸石推剪模型中颗粒与四周边界的接触力较大，颗粒受到的接触力主要为水平方向，并且也呈现从上到下逐渐增大的趋势．在模型的两端由于边界的约束作用，接触力较模型中部更大，接触力方向与水平方向有一定的夹角，这是由于治理后模型孔隙率更小，删除顶部边界后颗粒受到侧面挤压产生一定程度的回弹所导致的．

2．1．2 推剪过程模拟

在推剪试验的模拟过程中，使加载板以一定的速度向右挤压颗粒，加载板的速度为0．000 85 mm/时间步，换算为实际的推剪速度为0．017 mm/s，即现场试验的推剪速度为1 mm/min．图5为推剪破坏后的推剪模型试样．

图5 推剪破坏后的试样Fig．5 Specimen after shear failure

2．1．3 推力-位移曲线的模拟

图6为治理前后煤矸石推剪试验的推力-位移曲线与现场试验结果的对比．可以看出，模拟曲线的峰值推力和峰值推力点的位移都非常接近于试验值，模拟曲线的形态也比较接近试验曲线，都呈现了完整的全应力-应变曲线的形态．在起始阶段，模拟曲线与试验曲线基本重合;随后模拟曲线比试验曲线数据提升得略高，总体误差在5%以内，这是由于在PFC2D试样内部的颗粒单元全部为圆形所导致的试验数据差异．但总体上PFC2D模型能较好地模拟和反映现场试验情况，因此，也可以采用PFC2D的模拟结果对矸石散粒体内部的情况进行深入分析．

由图6可将推力-位移曲线大致分为4个阶段:①初始接触阶段(OA)，此阶段主要为煤矸石的挤密过程，曲线开始部分斜率较小，这主要是由试验初期钢板与煤矸石试样前侧的贴合过程所引起的;②弹性变形阶段(AB)，加载板与煤矸石颗粒接触紧密后，加载板所受到的作用力增大，因此曲线斜率增大．由于试样受到的推力作用较小，所以此阶段仍处于弹性变形阶段;③弹塑性变形阶段(BC)，此阶段煤矸石试样前侧的底端由于推力作用产生破裂，并且破裂面开始扩散，因此产生了一定的塑性变形．推力和位移不再呈线性关系，当水平推力增大时，位移明显增大，曲线斜率变小，试样在水平推力作用下破裂面进一步扩散．当推力达到一定程度时，破裂面贯通形成完整的滑裂面，试样剪切破坏;④应变软化阶段(C点后)，试样破坏后，由于试样内出现了贯通破裂面，因此出现推力随着位移的继续增大而减小的现象．

对比治理前后PFC2D模拟推力-位移曲线可以发现，治理后煤矸石的推力-位移曲线能更快地进入弹塑性变形阶段．在进入弹塑性阶段后，试样所承受的荷载与所发生的位移都更大，曲线峰值对应的推力和位移都比治理前要大．这是由于治理后的矸石山体密实度较治理前更高，因此在较小的位移下试样内便出现一定的破裂，进入弹塑性变形阶段．由于治理后的矸石山经过碾压作用提高了矸石体的力学特性，使得滑裂面在试样内开展速度较慢，并且需要更大的推力作用．达到破坏状态后，治理后矸石体的推力-位移曲线下降更为明显，这是由于治理后矸石体试样内会出现更为明显的滑裂面所导致的．

2．2 颗粒接触力分布

图7为PFC2D模拟治理前后推剪试样在推剪完成后颗粒间接触力的分布情况，其中虚线表示接触力的主要传递方向．可以发现，由于推力的作用，煤矸石颗粒受到较大的作用力，颗粒间作用力的传递方向是斜向下方，与水平方向存在一定的夹角，这是由于颗粒的上端没有任何约束的缘故．由于试样推剪破坏形成了贯通的滑裂面，推力更多地作用在滑裂体上，滑裂体沿着滑裂面发生剪切位移，远端颗粒对滑裂体具有一定的约束作用，因此在滑裂体边缘，存在接触力沿着滑裂面传递的现象．对比治理前后推剪模型内颗粒接触力分布情况可以发现，治理后推剪模型颗粒间的接触力主要集中在加载板的下半部分，并且接触力的分布集中区域更狭窄，与水平方向夹角更大，从而推剪试样更不容易被破坏．存在这种差异的原因主要是治理后推剪模型的煤矸石颗粒粒径较小，颗粒级配较均匀，并且试样更为密实，从而使接触力的传递区域更为集中．

图6 推力-位移曲线Fig．6 Curves of force-displacement

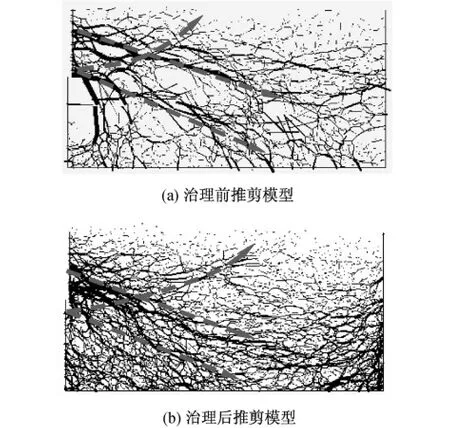
图7 推剪试验完成后接触力分布情况Fig．7 Contact stress distribution after push-shear test

模型在不同时间步长下最大接触力的变化情况如图8所示．由图可见，治理前推剪模型内最大接触力随着推力的增大而增大，直到试样破坏后，接触力减小．而治理后推剪模型内最大接触力增幅较小，随后略微降低．在开始阶段，治理后模型内的接触力是治理前的3．5倍，这是由于治理后模型孔隙率较小，造成颗粒间的挤压．但是在弹塑性变形阶段，治理前模型内的最大接触力比治理后更大，这是由于治理前的模型内存在较大量的大颗粒，而大颗粒的刚度大于细颗粒，并且治理前后模型进入弹塑性变形阶段的位移相差不大，从而造成了这种现象．

2．3 确定推剪试验的滑裂面

煤矸石不同于其他土体的特点是颗粒间不具有粘聚力，属于碎石类土．当采用推剪试验测定其抗剪强度参数时会遇到一个问题，即不能准确判断推剪破坏后的滑裂面，而滑裂面的确定是计算强度参数的重要步骤．颗粒流软件PFC2D可以较好地模拟得到离散颗粒的位移及速度等矢量，所以可采用颗粒流模型来确定推剪滑裂面．

图9为PFC2D模型颗粒位移矢量图，区域A为治理前推剪模型的推剪破坏区，区域内的平均位移为27．02 mm，虚线位置即为滑裂面;区域B为影响区，平均位移为11．53 mm;治理后推剪模型的推剪破坏区为区域C，区域内平均位移为24．59 mm;区域D为影响区，平均位移为10．95 mm;滑裂面为区域A与区域B的分界线．破坏区内的平均位移比影响区大2倍，影响区外的颗粒位移小于5 mm．

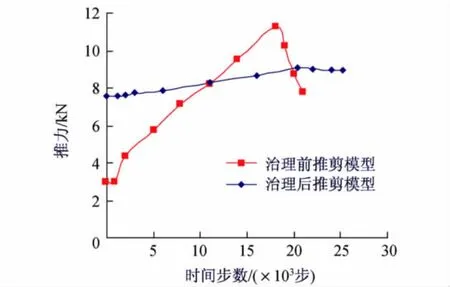
图8 不同时间步长下接触力变化Fig．8 Contact stress curve in different time steps

图9 PFC2D模型颗粒位移矢量图Fig．9 Displacement vector diagram of particle in PFC2Dmodel

可以看出，影响区的范围包含在推剪模型内，说明推剪模型大小选择适宜，并且治理后的推剪模型破坏区与影响区都大于治理前，因此，模型内的更多区域分担了外部作用力，使得模型具有更大的承载力．但治理后推剪模型内各区域的最大位移略小于治理前，这是由于治理后的推剪模型内存在更多的细颗粒，而细颗粒刚度较小，并且在推剪过程中更容易充填大颗粒间的空隙，同时大颗粒的粒径更小，所受作用力也更小，因而导致了治理后推剪模型内具有更小的位移．

2．4 推剪速率对抗剪强度的影响

在推剪试验中，需要控制千斤顶以恒定的速率对试样进行推剪，但是不同试验往往采用不同的推剪速率．为了研究推剪速率对抗剪强度的影响，本研究采 用 PFC2D程 序 分 别 以 0．5，1．0，1．5，2．0，3．0 mm/min的推剪速率对煤矸石试样进行推剪，结果如图10和图11所示．试验结果表明，推力-位移曲线的峰值推力与推剪速率成线性正比关系，峰值推力对应的位移与推剪速率成幂函数关系，并随推剪速率增大而减小．通过模拟确定各推剪速率下模型的滑裂面，计算得出抗剪强度参数，可以发现粘聚力与内摩擦角均随推剪速率的增大而增大，粘聚力和内摩擦角分别与推剪速率成指数函数和幂函数关系．通过对各拟合曲线函数关系式的对比，可以发现治理后煤矸石推剪试验中推剪速率对抗剪强度参数计算结果的影响更大，从而说明强度特性越好的土体的抗剪强度参数计算结果对推剪速率越敏感．

图10 峰值推力、位移随推剪速率的变化Fig．10 Variation regularity of peak force and displacement along push-shear rate

图11 抗剪强度试验结果随推剪速率的变化Fig．11 Variation regularity of push-shear rate and shear strength

3 结论

(1)对现场推剪试验中不同密实度、不同级配的煤矸石推剪试样制备过程和加载过程进行了PFC2D模拟;通过多次试算选取了模拟煤矸石颗粒以及模型边界所用的参数，模拟得到的推力-位移曲线与试验值基本吻合，说明颗粒流仿真模拟能够对煤矸石推剪试验进行细观方面的分析．

(2)对模拟得到的推力-位移曲线进行分析，将其分为初始接触、弹性变形、弹塑性变形、应变软化4个阶段．治理后的煤矸石能更快进入弹塑性阶段，并且在推剪过程中具有更大的塑性变形．

(3)治理前后推剪模型在试样制备完成后的接触力有明显不同，治理前接触力分布大致符合自重应力的分布特点，治理后由于碾压作用，接触力呈倒月牙形分布．推剪完成后颗粒接触力的传递方向与水平方向成一定夹角向下，在滑裂体边缘存在接触力沿着滑裂面传递的现象．治理后推剪模型接触力的集中分布区域更狭窄，与水平方向的夹角更大．

(4)根据位移的大小将推剪模型分为破坏区和影响区，影响区外的颗粒位移小于5 mm，说明推剪模型尺寸取值合理．根据颗粒位移矢量图确定了推剪试验的滑裂面，解决了煤矸石推剪试验中滑裂面难以确定的问题．

(5)推剪速率对推剪试验结果有一定影响，推剪速率越大，推力-位移曲线中的峰值推力线性增大，峰值推力对应的位移减小，且二者成幂函数关系．通过试验计算得出的粘聚力和内摩擦角随推剪速率的增大而减小，并且与推剪速率分别成指数函数和幂函数关系．推剪速率对粘聚力的计算结果影响更为明显，并且煤矸石抗剪强度越大，对推剪速率的敏感性越高．

［1］ 刘松玉，邱钰，童立元，等．煤矸石的强度特征试验研究［J］．岩石力学与工程学报，2006，25(1):199-205．

［2］ 贺建清，靳明，阳军生．掺土煤矸石的路用工程力学特性及其填筑技术研究［J］．土木工程学报，2008，41(5):87-93．

［3］ 臧亚君，刘东燕，彭文轩，等．重庆矿区矸石山体特性现场试验研究［J］．岩土工程学报，2009，31(4):558-563．

［4］ 李晓，廖秋林，赫建明，等．土石混合体力学特性的原位试验研究［J］．岩土力学与工程学报，2007，26(12):2006-2013．

［5］ 吴硕，李晓，赫健明．土石混合体原位水平推剪试验［J］．岩土工程技术，2007，21(4):184-189．

［6］ POWRIE W，NI Q，HARKNESS R M，et al．Numerical modelling of plane strain tests on sands using a particulate approach［J］．Geotechnique，2005，55(4):297-306．

［7］ ZHANG J， YASUFUKU N， OCHIAI H． A few considerations of pullout test characteristics of geogrid reinforced sand using DEM analysis［J］．Geosynthetics Engineering Journal，2007，22(11):103-110．

［8］ 周健，史旦达，贾敏才，等．砂土单调剪切力学性状的颗粒流模拟［J］．同济大学学报:自然科学版，2007，35(10):1299-1304．

［9］ 史旦达，周健，刘文白，等．砂土直剪力学性状的非圆颗粒模拟与宏细观机理研究［J］．岩土工程学报，2010，32(10):1557-1565．

［10］ 杨贵，肖杨，高德清．粗粒料三维颗粒流数值模拟及其破坏准则研究［J］．岩土力学，2010，31(S2):402-406．

［11］ 贾学明，柴贺军，郑颖人．土石混合料大型直剪试验的颗粒离散元细观力学模拟研究［J］．岩土力学，2010，31(9):2695-2700．

［12］ 严颖，季顺迎．碎石料直剪实验的组合颗粒单元数值模拟［J］．应用力学学报，2009，26(1):1-7．

［13］ 孟云伟，柴贺军，贾学明．石笼挡土墙的颗粒离散元细观力学模拟研究［J］．岩土力学，2010，31(8):2677-2684．

［14］ CUNDALL P A，STRACK O D L．A discrete numerical method for granular assemblies［J］． Geotechnique，1979，29(1):47-65．

［15］ HOOMANS B PB，KUIPERS JA M，BRIELSW J，et al．Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidized bed:A hard-sphere approach［J］．Chemical Engineering Science，1996，51(1):99-118．

Mesomechanical Simulation of Push-Shear Tests on Coal Waste with Particle Flow Code

DUAN Wei1，2， ZHANG Meng-xi1
(1．Department of Civil Engineering，Shanghai University，Shanghai 200072，China;2．Shanghai Urban Construction Municipal Engineering(Group)Co．Ltd．，Shanghai 200065，China)

TU 413．1

A

1007-2861(2012)05-0531-07

10．3969/j．issn．1007-2861．2012．05．017

2011-08-31

张孟喜(1963～)，男，教授，博士生导师，博士，研究方向为新型土工加筋技术及环境岩土工程等．E-mail:mxzhang@staff．shu．edu．cn