树依能量的排序
2012-10-16王文环徐薇薇
王文环, 徐薇薇
(上海大学理学院,上海200444)
树依能量的排序
王文环, 徐薇薇
(上海大学理学院,上海200444)
令Tn是顶点个数为n的树的集合.已有学者针对Tn中树依能量从小到大的排序提出了两个猜想,其中一个猜想是Tn中两个图能量的比较,另一个是Tn中当n≥7 117 599时的第10小至第12小能量树.该文证明这两个猜想成立;确定Tn中当n≥7 117 599时前12个具有较小能量的树.
树;排序;最小能量
Abstract:Let Tnbe a set of trees with n vertices.The increasing orders in terms of the minimal energies of the trees in Tnhad been considered and two conjectures were proposed.The first one is the comparison of the energies of two graphs in Tn.The other is about the trees with the 10th to 12th minimal energies for n≥7 117 599.This paper proves that the two conjectures are true,and obtain the first 12 trees within Tnfor n≥7 117 599.
Key words:tree;ordering;minimal energy
设G为具有n个顶点的简单图.在Hückel分子轨道(Hückel molecular orbit,HMO)意义下,图 G 的能量定义为

式中,λ1,λ2,…,λn为 φ(G,x)=0 的 n 个根,这里

为G的特征多项式[1],I为n阶单位矩阵,A(G)为G的邻接矩阵,a0,a1,…,an为 φ(G,x)的系数.由于A(G)是对称的,因此每个λi(1≤i≤n)是实的.
图的能量是图所对应的共轭分子化学结构和热力学稳定性之间的一个桥梁[2].在化学图论中,图的能量越大(小),相应化合物的热力学稳定性越强(弱).基于图能量的实际意义和理论价值,在化学图论中,研究具有极值能量的图具有十分重要的地位和意义[3].进一步了解图能量的数学概念和性质可参见文献[1-2].
研究图依能量排序的一个有效方法是系数比较法,即对所考虑的图根据其特征多项式的系数绝对值的大小进行比较[4-10].树是图论中具有典型意义的一种图类.令Tn是顶点个数为n的树的集合,对Tn中树依能量从小到大(从大到小)的排序已有一些研究结果.利用系数比较法,Gutman[4]得到了Tn中前 4个具有较小能量的树.Li等[9]拓宽了Gutman[4]的结果,得到了 Tn中当 n≥6时的第5小能量树,给出了Tn中当n≥14时的第6小能量树.但是,系数比较法具有一定的局限性,在某些情况下,对图的能量比较失效.例如,Li等[9]就未能得到Tn中第7小能量树.
除了系数比较法,另外一个有效的方法是利用零点定理来比较两个图的能量.因此,人们极大地拓宽了图依能量的排序范围[11-14].利用上述两种方法,对Tn中树,当 n≥46,7 117 598≥n≥26 和25≥n≥18时,Wang等[11]分别得到了前9个、前12个和前11个具有较小能量的树且进行了排序;当17≥n≥7时,Wang等[11]也得到了许多具有较小能量的树且进行了排序.
虽然零点定理可成功地用来比较两个图的能量,但也具有其局限性.为了克服系数比较法和零点定理的局限性,需要引入新的有效方法来比较图的能量.例如,Huo等[15]发展了一种新方法,即直接从Coulson积分公式出发,利用实分析的方法比较了两个图的能量大小.在文献[11]中,零点定理不能用来比较Tn中当n≥7 117 599时两个候选图的能量大小.对此,Wang等[11]只是给出两个猜想,其中一个是两个候选图能量的比较,另一个是Tn中当n≥7 117 599时的第10小至第12小能量树.
1 准备工作
记Tn中直径为 d的树的集合为 Tdn,其中2≤d≤n-1.令Pn是顶点个数为n的路,Pn上的顶点依顺序标号为 v0,v1,…,vn-1.令 Tdn(n1,n2,…,nd-1)为在Pd+1上的顶点 vi(i=1,2,…,d-1)上分别加

ni(ni≥0)条悬挂边后得到的树.显然,d -1,Tdn(n1,n2,…,nd-1)∈ Tdn.T4n(n -5,0,0),Un=T4n(n -6,0,1),Hn=T4n(0,n -5,0),Qn'=T4n(n -6,1,0).
令T1和T2为Tn中的两棵树.为了简单起见,引入符号“⇀”,“⇌”和“→→”如下:

当n≥14时,Tn中前8个具有较小能量的树为

式中等号成立当且仅当n=8.下面用符号(◇)来替代式(4).式(4)中前 4 个图由 Gutman[4]得到,第 5和第6个图由Li等[9]得到,第7和第8个图由Wang等[11]得到.此外,当 n≥46 时,Wang 等[11]得到了 Tn中前9个具有较小能量的树,即(◇)⇀Hn⇀T,其中T不等于Hn和(◇)中的图.
对于不等式中的T,假定T∈Tn且T不是不等式中已列出的图.利用零点定理,Wang等[11]得到了如下引理1.
引理1 当7 117 598≥n≥11时,Tn4(n-8,0,3)⇀Qn'.
在引理1的基础上,当7 117 598≥n≥59时,Wang等[11]得到了 Tn中前12个具有较小能量的树,即有如下定理1.
定理1 令T∈Tn且7 117 598≥n≥59,则
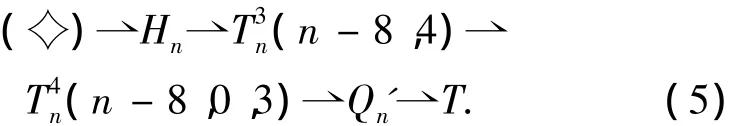
由于零点定理的局限性,在引理1中,不能证明当 n≥7 117 599 时,T4n(n -8,0,3)⇀Qn'成立.因此,Wang等[11]给出了如下2个猜想.
猜想1 当 n≥7 117 599,T4n(n -8,0,3)⇀Qn'.猜想2 令T∈Tn且n≥7 117 599,则

本研究将利用根与特征多项式系数之间的关系,严格证明猜想1和猜想2成立,从而确定了Tn中当n≥7 117 599时前12个具有较小能量的树.
2 主要结果
首先证明猜想1成立,则有如下引理2.
引理2 当 n≥11 时,T4n(n-8,0,3)⇀Qn'.
证明 文献[11]已得到

不妨令 z1<z2<z3.

最后,由图能量的定义式(1)以及式(7)~(10),可得


引理2证毕.
由文献[11]和本研究的引理2,下面证明猜想2成立,则有如下定理2.

由文献[11]的引理12和引理14,当 T∈{T3n(n1,n2),T4n(n1,0,n3)}且 n≥59,其中 n2≥5,n3≥4 时,有 Qn'⇀T3n(n -9,5)→→T.又由文献[11]的引理 19,当T∈Tn{T3n(n1,n2),T4n(n1,0,n3)}且 n≥59 时,有Qn'⇀T.因此,对于T∈Tn且T不为式(11)中所列出的图,当 n≥59时,皆有 Qn'⇀T成立.显然,由式(12)~(14),定理2成立.
定理2拓宽了文献[11]的排序范围,当 n≥7 117 599时,得到了Tn中前12个具有较小能量的树,比原有文献多了3个.由定理1和定理2可以发现,Tn中当7 117 598≥n≥59和n≥7 117 599时,前12个具有较小能量的树及其排序是相同的,因此有如下推论1.

推论1弥补了定理1的不足,完全得到了Tn中当n≥59时前12个具有较小能量的树并进行了排序.同时,将文献[11]的排序结果进行了推广,使排序结果更加完满.
[1] CVETKOVIC D M,DOOB M,SACHS H.Spectra of graphs theory and application[M].New York:Academic Press,1980.
[2] GUTMAN I,POLANSKY O.Mathematical concepts in organic chemistry[M].Berlin:Springer-Verlag,1986.
[3] 唐熬庆.分子轨道图形理论[M].北京:科学出版社,1980.
[4] GUTMAN I.Acyclic systems with extremal Hückelπelectron energy[J].Theoretica Chimica Acta,1977,45:79-87.
[5] ZHANG F,LI H.On acyclic conjugated molecules with minimal energies [J].Discrete Applied Mathematics,1999,92(1):71-84.
[6] HOU Y P.Unicyclic graphs with minimal energy[J].Journal of Mathematical Chemistry,2001,29(3):163-168.
[7] ZHANG J B,ZHOU B.On bicyclic graphs with minimal energies[J].Journal of Mathematical Chemistry,2005,37(4):423-431.
[8] LI X L,ZHANG J B.On bicyclic graphs with maximal energy[J].Linear Algebra and Its Applications,2007,427(1):87-98.
[9] LI N N,LI SC.On the extremal energies of trees[J].MATCH-Communications in Mathematical and in Computer Chemistry,2008,59(2):291-314.
[10] LI S,LI X,ZHU Z.On tricyclic graphs with minimal energy[J].MATCH-Communications in Mathematical and in Computer Chemistry,2008,59(2):397-419.
[11] WANG W H,KANG L Y.Ordering of the trees by minimal energies [J]. Journal of Mathematical Chemistry,2010,47(3):937-958.
[12] GUO J M.On the minimal energy ordering of trees with perfect matchings[J].Discrete Applied Mathematics,2008,156(14):2598-2605.
[13] WANG W H,KANG L Y.Ordering of the trees with a perfect matching by minimal energies[J].Linear Algebra and Its Applications,2009,431(5/6/7):946-961.
[14] LIU Y.Some results on energy of unicyclic graphs with n vertices[J].Journal of Mathematical Chemistry,2010,47(1):1-10.
[15] HUO B F,JI SJ,LI X L.Note on unicyclic graphs with given number of pendent vertices and minimal energy[J].Linear Algebra and Its Applications,2010,433(7):1381-1387.
Tree Ordering According to Minimal Energies
WANG Wen-huan,XU Wei-wei
(College of Sciences,Shanghai University,Shanghai 200444,China)
O 157.6
A
1007-2861(2012)05-0480-04
10.3969/j.issn.1007-2861.2012.05.008
2011-09-15
国家自然科学基金资助项目(11001166);上海市重点学科建设资助项目(S30104)
王文环(1975~),女,副教授,博士,研究方向为图论及其应用.E-mail:whwang@shu.edu.cn
