基于SAR测量的改进型VIE降雨反演算法

郑 和， 谢亚楠， 万智龙， 刘文渊

(上海大学通信与信息工程学院，上海200072)

基于SAR测量的改进型VIE降雨反演算法

郑 和， 谢亚楠， 万智龙， 刘文渊

(上海大学通信与信息工程学院，上海200072)

提出一种新型降雨反演算法，该算法是对沃尔塔积分方程(Volterra integral equation，VIE)降雨反演算法的改进．首先，对雷达接收到的回波数据进行预处理，得到降雨起点和降雨宽度等信息;然后，仅利用沃尔塔积分反演算法处理少量特定区域，通过深度挖掘数据变化的规律来分析得出降雨分布的类型和降雨速率;最后，根据通常研究对象的分布对称性，结合已经获得的信息反演得到整个区域的降雨分布情况．通过仿真结果可知，该算法高效、计算速度快，并且具有较高的精度．

反演算法;沃尔塔积分方程改进算法;面向统计反演模型;降雨;合成孔径雷达

Abstract:This paper proposes a new type of rainfall retrieval algorithm，which improves the method using the Volterra integral equation(VIE)．The proposed algorithm makes pre-analysis on the data received by synthetic aperture radar to get information such as the rainfall start point and the scope of the rain．The VIE retrieval algorithm is then applied in a short distance to get information of the rain distribution．Further analysis is then made on the information obtained in the previous step to find parameters such as shape of the rain and the rain rate．According to the most commonly studied rainfall distributions that are symmetric，the rainfall distribution is obtained．Simulation results show that the proposed algorithm is effective and efficient，with high accuracy．

Key words:inversion algorithm;improved Volterra integral equation(VIE)method;statistic oriented inversion model;rainfall;synthetic aperture radar(SAR)

降雨不仅影响人们的日常生活，而且改变了全球的热分布，因此对全球范围内的降雨情况进行监控，对气象和水循环研究都具有重要的意义．常用的降雨监测方法主要有2种:一种是使用地基雷达，但是地基雷达的观测范围小，无法实现针对全球范围的有效监测;另外一种是采用星载雷达进行监测，主要有红外遥感和微波遥感．目前全球唯一在运行的是1997年美国和日本联合研制的“热带降雨使命(tropical rainfall measuring mission，TRMM)”卫星［1］，这颗卫星已经运行了十几年，积累了大量的降雨数据．由于TRMM的“寿命”将尽，美国和日本联合研制的“全球降雨使命(global precipitation mission，GPM)”卫星也将发射．文献［2-3］分别对因测雨雷达波束不均匀填充带来的误差和后向迭代降雨反演算法的适用性进行了分析．而且，文献［4］提出了对星载测雨雷达相控阵天线实现低副瓣的粒子群算法．

合成孔径雷达的回波数据含有丰富的降雨区域和地面背景散射信息，能够准确得到地面的降雨分布情况．1999年中国首颗SAR卫星开始工程研制，但中国SAR卫星都没有气象观测任务．由于测雨雷达(precipitation radar，PR)造价昂贵、元器件采购困难，而且X波段和Ku波段很接近，因此探索如何将X-SAR用于全球降雨监测，对于测雨理论的补充和满足实际需要都有重要意义．Moore等［5-6］针对用于测雨的合成孔径雷达，从雷达方程、最小可测雨量等方面进行了研究;Pichugin等［7］提出了VIE反演算法并进行了验证，该算法数学推导严谨，但是计算繁杂，运算量很大;Weinamn和 Marzano等［8-9］分别详细论述了面向模型的反演算法，以及将球面波简化为平面波带来的误差，并把VIE反演算法和面向模型反演算法进行了比较;Marzano等［10］进一步论证了合成孔径雷达测雨的能力，并且给出了根据雨区衰减补偿回波图像的方法;Xie等［11-12］提出了对于面向模型反演算法的改进并通过对雨滴形状的分析来提高反演精度．本工作在上述研究的基础上，为了克服VIE反演算法计算复杂、运算量大的缺点，结合回波数据预处理、VIE反演算法以及雨区分布的对称性，提出了一种新型反演算法，达到了高效、准确反演降雨量的目的．

1 归一化雷达反射截面方程

归一化雷达截面来源于两个方面:地面散射以及雷达波面遇到降雨粒子带来的体散射．X-SAR测雨模型如图1所示．本模型忽略地球曲率，不考虑波束宽度，将球面波简化为平面波来处理．则归一化雷达反射截面(normalized radar cross section，NRCS)为［8］

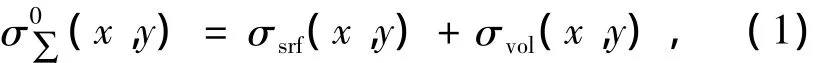
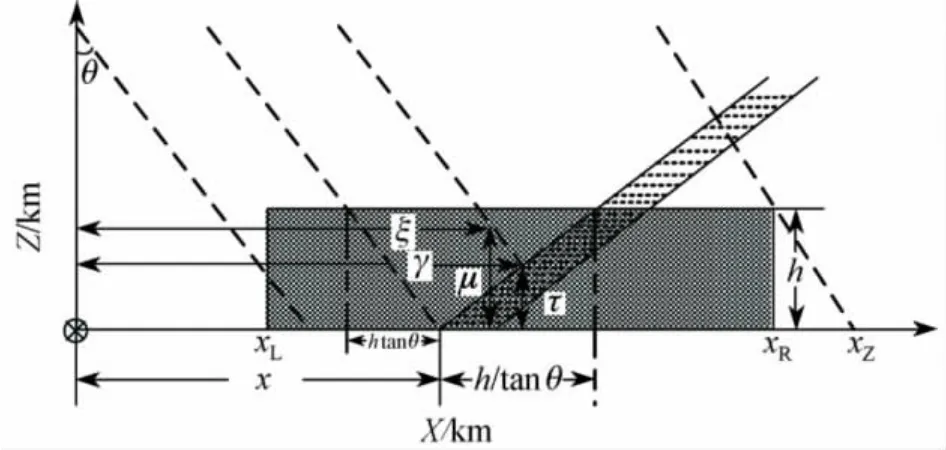
图1 降雨反演算法原理图Fig．1 Rainfall retrieval method schematic diagram

式中，

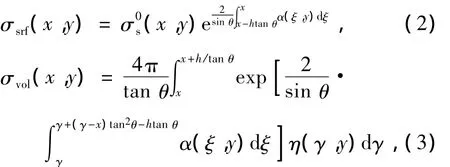
其中σ0∑为归一化雷达反射截面，σsrf为面散射回波，σvol为体散射回波．如图1所示，x为与观测点之间的横向距离，y为与观测点之间的纵向距离，方向垂直指向纸张(向里)，Z轴表示高度．(ξ，μ)为体散射波回波路径上任意一点的坐标，(γ，τ)为波面处散射粒子的坐标，h为降雨区的高度，θ为入射角．xL为雨区开始位置的横坐标，xR为雨区终止位置的横坐标，xZ为体散射波结束位置的横坐标．

2 改进的VIE降雨反演算法

由雷达测雨的近似公式［8］可知:

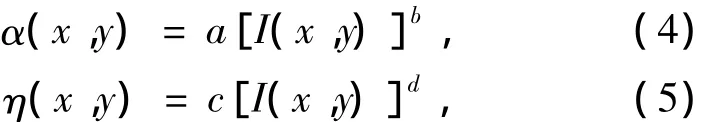
式中，系数a，b，c，d与雷达波的频率、水滴的大小和分布、温度等条件是密切相关的;α为降雨对雷达波的衰减;I为降雨强度;η为降雨对雷达波束的散射．对于降雨分布，Weinman等［8］提出了几种典型的系数取值:a=2．6 ×10－3，b=1．11，c=300，d=1．35．如果把式(4)和(5)代入到式(1)中，可得到一个非线性的积分方程．应用VIE反演算法对其进行处理，使得方程简化为线性的第二类沃尔塔积分方程，从而实现降雨的反演，但是，使用上述方法使计算复杂度大幅增加．本工作提出的改进的VIE降雨反演算法有效解决了这个问题．

2．1 VIE反演算法推导

引入函数［7］

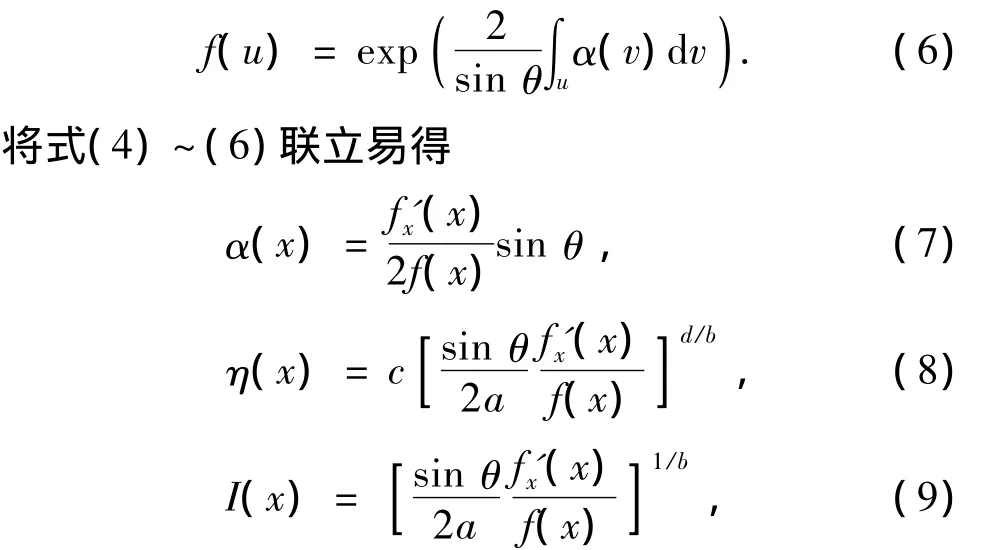
其中fx'(x)为f(x)对x的一阶导数．这里没有考虑y，是因为现在处理的是图像的同一行数据．处理不同行数据就可以得到整个分布．考虑到

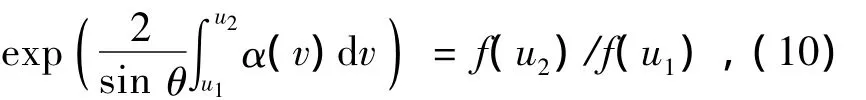
则将式(4)～(10)代入式(1)，并将观测点从x移到x+h tan θ，可得［9］

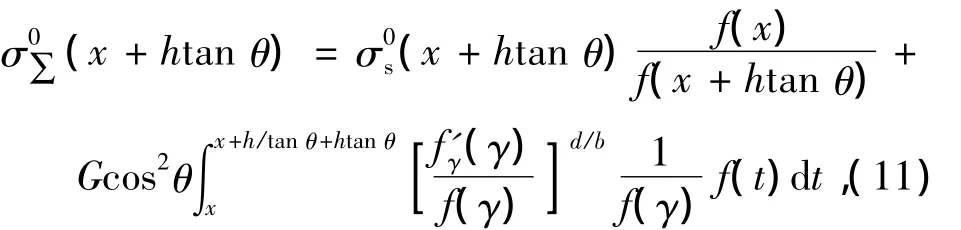
式中，

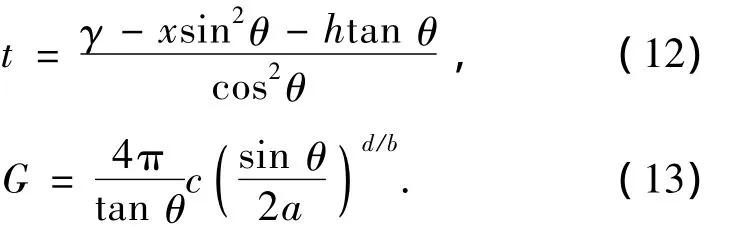
由式(11)解出f(x)得

情况三：如图6，作△ADB的外接圆⊙E，假设E在AB上，连接DE，在⊙E中，∠DEA=2∠DBA=60°，又因为DE=AE，所以△ADE为等边三角形，所以AD=AE，因为AB=2AE，AC=AB，所以AC=2AE，因为AD=AE=CD，所以AC=AD+CD，在△ACD中AC

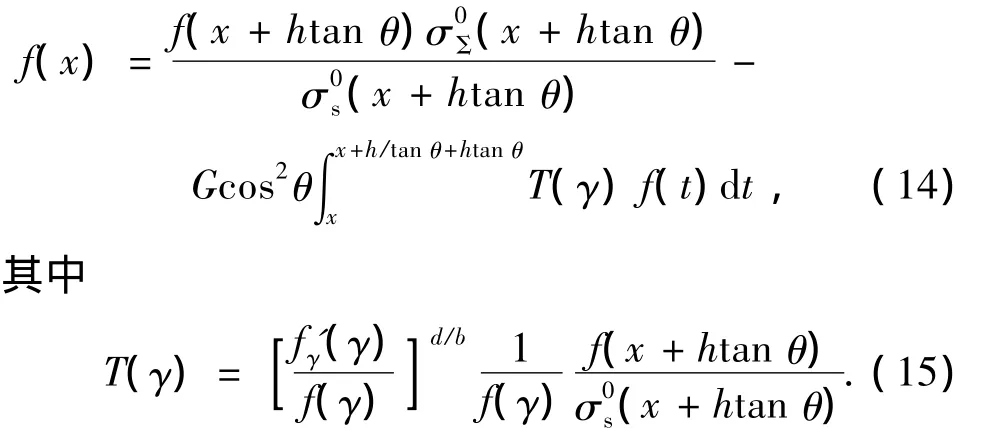
通过解第二类沃尔塔积分方程就可以解出式(14)．具体步骤如下:在区间x＞xZ，通过图1可知，反射波不经过降雨区，即α=0，代入式(6)易知［9］，

在区间 xZ－h tanθ≤x≤xZ，由式(12)和(14)得γmin＞xZ，由式(16)得 f(γ)=1，则 fγ'(γ)=0，则由式(14)易知［9］，

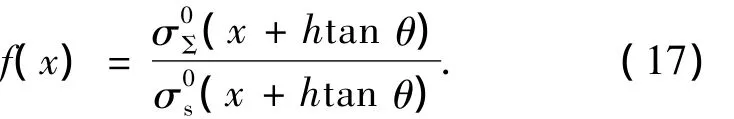
如上所述类推，即可得到f(x)的分布情况;然后采用数值积分的方法，利用插值得到所有分布;最后代入式(9)即得反演结果．对于上述反演算法，每隔h tanθ距离，反演的表达式都不相同．而且在计算式(14)时，需要使用数值积分，比如使用Newton-Cotes公式进行数值积分计算．由于计算科特斯系数的限制，进行数值积分的点数不宜太多，这样缺少的信息只能通过插值来获得，因此带来了较大的误差．而且很显然，随着降雨区域长度的增加，VIE反演算法的计算量和计算的复杂程度一直在大幅增加，这大大降低了其反演的处理能力．

2．2 VIE反演算法的改进

为了解决上述VIE算法存在的问题，本工作提出了改进算法，以达到不仅计算量小而且高效准确的目的．本算法的核心思想是通过对回波数据的预处理，得到降雨起点、回波最小值、降雨区域宽度等信息;然后，通过在一个特定的区域使用VIE反演算法，获得降雨分布的形状和降雨速率等信息．由于通常将降雨区域视为对称分布，这样根据上面的两个步骤就可以对称得出整个降雨区域的分布．这种方法随着降雨区域的增大，计算量增加不多且保证了反演精度．具体步骤如下:

(1)反演降雨起始点x^0和回波最小值x^min，σSAR(x)＜{An(σSAR)－3Rn［σSAR－An(σSAR)］}，(18)式中，An和Rn值分别表示在x点前5个回波数值的平均值和均方根［4］．当x满足上述条件时，即为降雨起始点x^0．

通过比较回波数据就可以得到回波最小值x^min．但是为了避免随机噪声带来的影响导致误判，需要多考虑两个参数，D1和D2．D1为对回波数据进行一阶求导，D2为对回波数据进行二阶求导．根据拐点的特点容易得到，在拐点处D1=0，D2值最大，

(2)反演降雨宽度w^．根据统计公式，对于矩形分布，

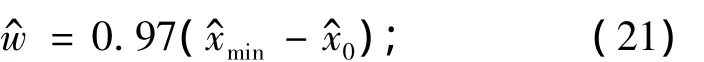
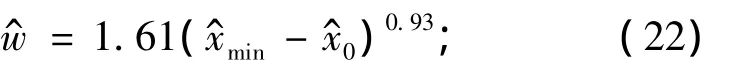
对于三角形分布，对于梯形分布，采用矩形分布和三角形分布的加权平均来表示，即

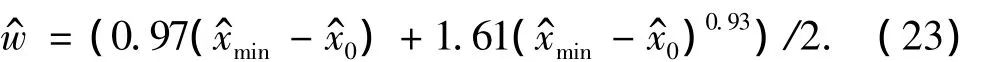
(3)反演降雨水平分布的形状和降雨速率．

如式(16)和(17)所示，本算法在处理降雨区域时，仅仅在区间长度为h tanθ这个较小的区域使用VIE反演算法，然后对其他数值进行填充．通过分析数据变化的规律，反演降雨水平分布的形状和降雨速率．接着，代入式(9)中得到区间(0，xZ)降雨的分布类型，存储于数组I(·)中并设Δx为计算步长．结合矩形分布、梯形分布和三角形分布的特点易知，若k=ΔI(x)/Δx＞30，则可以认为斜边斜率足够大而视为矩形分布．对于矩形分布，斜边的斜率理论上是无穷大，但是由于数值运算求导的限制，实际运算出的斜率与网格的划分有关，这里选取一个典型值．如果不符合上述条件，对于I(·)中所有的点计算以下两个参数:

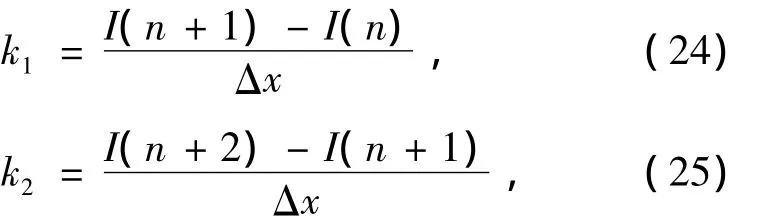
式中，k1和k2意味着I(x)数值内每个点的斜率，I(n)表示数组I(·)中的任一数值．根据梯形分布和三角分布的特点易知，如果出现k1≥2k2且k2≥0，说明是梯形分布;如果k1≥2k2且k2＜0，说明是三角形分布．对数组I(·)进行处理，记数组中第一个拐点为I(M)，第一个不为零的点为I(N)，则对于梯形分布，I(M)为反演的降雨量;对于矩形分布，查找I(·)的最大值即为反演的降雨量;对于三角形分布，如果 I(M)和 I(N)之间的距离大于等于w^/2，则I(M)是最大降雨量．否则，根据斜率相等的原则，填充数组I(·)，使得I(M)和 I(N)之间的距离等于w^/2，此时I(M)是三角形分布的最大降雨量．

(4)反演整个区域的降雨水平分布．

如上所述，降雨分布的起点、终点、形状、大小都已经确定，下面分不同情况将降雨分布信息反演出来．对于矩形分布，给定起点、终点和大小即可确定;对于梯形分布，左侧斜边的长度为L1=(M－N)Δx，则梯形的上底宽度为w1=w^－2L1;对于三角形分布，如果L1＜w^/2，说明左侧三角形并没有达到降雨速率的最大值．由此依据三角形左侧图形斜率相等，将左侧三角形补充完整，然后左右对称即可．反之，则直接在L1=w^/2处左右对称．

(5)补偿降雨水平分布区域的位置．

从对I(x)的处理过程可知，反演出的降雨起点并不准确，但式(18)已经得到了降雨的起始点．这样将整个区域对应进行降雨位置调整即可得到最终的反演结果．

3 仿真结果

下面分别对常见的矩形降雨分布、梯形降雨分布和三角形降雨分布进行仿真，验证算法的可靠性．重点探讨对VIE反演算法的改进效果，并对此进行仿真验证，相关应用会在今后进行进一步研究．

降雨分布类型为矩形分布，降雨起点为8．34 km，降雨宽度为10 km，降雨速率为20 mm/h．反演结果如下:降雨分布类型为矩形分布，降雨起点为7．902 km，降雨宽度为 10．024 km，降雨速率为19．29 mm/h，降雨速率反演误差为 3．55%(见图2)．

降雨分布类型为梯形分布，降雨起点为8．34 km，降雨宽度为10 km，左侧边斜率为6．7，降雨速率为20 mm/h．反演结果如下:降雨分布类型为梯形分布，降雨起点为 8．510 km，降雨宽度为9．456 km，降雨速率为17．67 mm/h，左侧边斜率为5．8，降雨速率反演误差为11．65%(见图3)．

降雨分布类型为三角形分布，降雨起点为8．34 km，降雨宽度为10 km，降雨速率为20 mm/h．反演结果如下:降雨分布类型为三角形分布，降雨起点为8．206 km，降雨宽度为10．614 km，降雨速率为18．73 mm/h，降雨速率反演误差为6．35%(见图4)．

仿真结果分析:上述仿真设定的雷达入射角为40°，地面最大面散射为－5 dB，是常见的典型取值．仿真实际的降雨起点和降雨宽度以及降雨速率的选取不影响仿真结果．上述结果表明:①梯形分布和三角形分布的降雨反演误差均在10%以内．梯形分布由于在数据预处理时无法获得准确的统计公式，导致反演误差稍大，达到11．65%，但是仍能满足反演算法要求，拟合出梯形分布公式则可以大幅提高梯形分布反演精度．本算法的反演精度与VIE反演算法的精度11%左右［7］相当;②本算法仅仅计算长度为h tanθ的数据，然后通过数据预处理和对称来得到整体降雨水平分布;而VIE反演算法需要计算(0，xZ)内的降雨分布，且每隔h tanθ的长度，都需要重新计算式(14)．所以，本算法要比VIE算法的计算量小得多，且随着雨区宽度的增大，计算效率高的优势将更加明显．

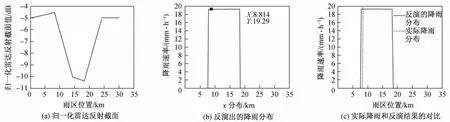
图2 矩形降雨分布反演结果Fig．2 Retrieved results of rectangular rainfall distribution

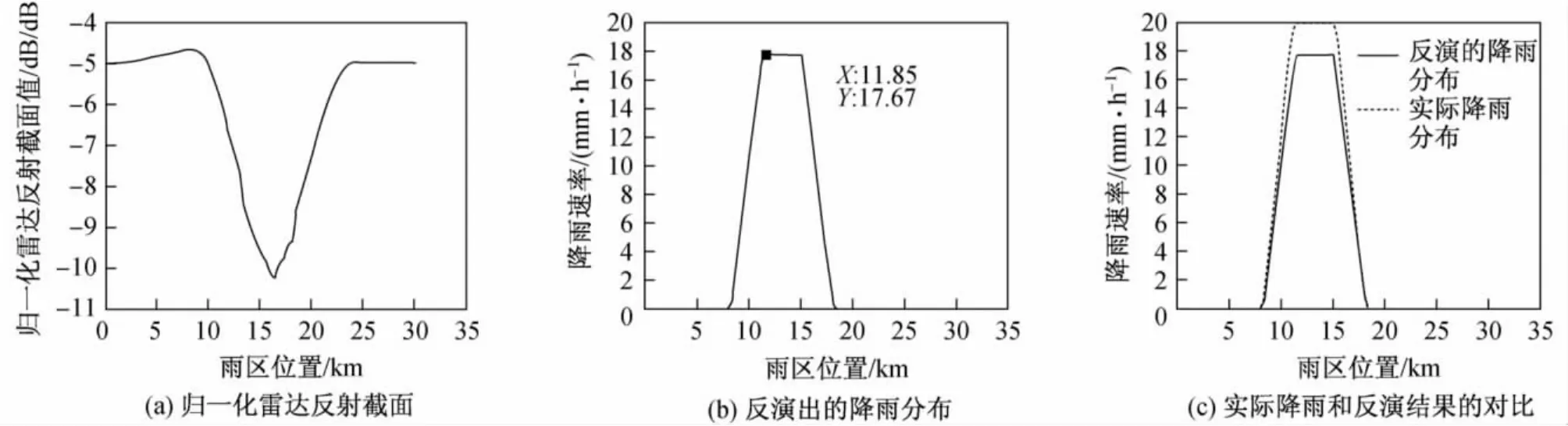
图3 梯形降雨分布反演结果Fig．3 Retrieved results of trapezoidal rainfall distribution

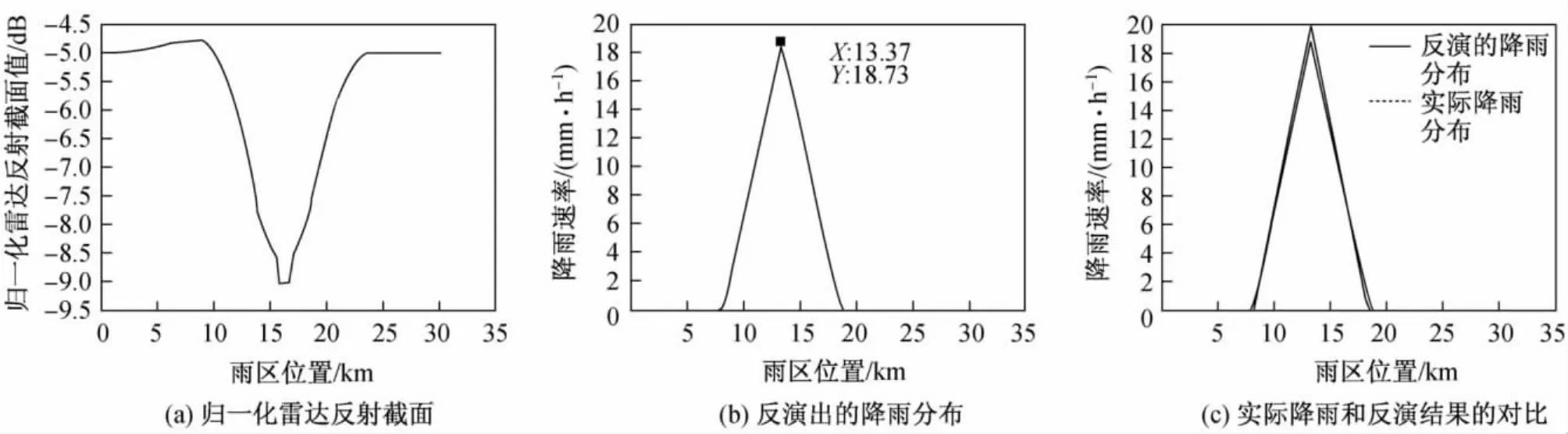
图4 三角形降雨分布反演结果Fig．4 Retrieved results of triangle rainfall distribution

4 结束语

本工作分析了VIE降雨反演算法的过程和特点，对算法存在的问题进行了讨论，解决了原算法存在的数学计算过程复杂、计算量大等问题;提出了依据回波预处理、降雨区域的对称性并结合VIE反演算法来反演降雨的改进反演算法．从仿真结果可以看出，该算法的反演精度在10%左右，与VIE反演算法精度相当．而且从上述理论分析可知，本算法能大大简化数学运算过程，大幅降低运算量．针对本算法的下一步工作是对相关应用情况进行研究．

［1］ MENEGHINI R，JONES J A． Standard deviation of spatially averaged surface cross section data from the TRMM precipitation radar［J］．IEEE Geoscience and Remote Sensing Letters，2011，8(2):293-297．

［2］ DURDEN SL，TANELLI S．Predicted effects of nouniform beam filling on GPM radar data［J］．IEEE Geoscience and Remote Sensing Letters，2008，5(2):308-310．

［3］ SETO S， IGUCHI T． Applicability of the iterative backward retrieval method for the GPM dual-frequency precipitation radar ［J］． IEEE Transactions on Geoscience and Remote Sensing，2011，49(6):1827-1838．

［4］ 徐锋明，孟令琴，谢亚楠．基于改进的粒子群算法实现阶梯幅度量化相控阵天线的低副瓣［J］．上海大学学报:自然科学版，2010，16(4):361-366．

［5］ ATLAS D， MOORE R K． The measurement of precipitation with synthetic aperture radar［J］．Journal of Atmospheric and Oceanic Technology，1987，4(3):368-376．

［6］ MOORE R K，MOGILI A， FANG Y， et al． Rain measurement with SIR-C/X-SAR ［J］．Remote Sensing of Environment，1997，59(2):280-293．

［7］ PICHUGIN A P，SPIRIDONOV Y G．Spatial distributions of rainfall intensity recovery from space radar images［J］．Sov J Remote Sens，1991，8:917-932．

［8］ WEINMAN JA，MARZANO F S．An exploratory study to derive precipitation over land from X-band synthetic aperture radar measurements［J］．Journal of Applied Meteorology and Climatology，2008，47:562-575．

［9］ MARZANO F S，WEINMAN J A．Inversion of spaceborne X-band synthetic aperture radar measurements for precipitation remote sensing over land ［J］．IEEE Transactions on Geoscience and Remote Sensing，2008，46(11):3472-3487．

［10］ MARZANO F S，MORI S，WEINMAN J A．Evidence of rainfall signatures on X-band synthetic aperture radar imagery overland［J］．IEEE Transactions on Geoscience and Remote Sensing，2010，48(2):950-964．

［11］ XIE Y N，HUAN J P，TAO Y．Study on the algorithm to retrieve precipitation with X-band synthetic aperture radar［J］．Acta Meteorologica Sinica，2010，24(5):614-621．

［12］ XIE Y N，ZHOU X L，YANG Z D．Error analysis of nonspherical raindrops on precipitation measurement［J］．Journal of Shanghai University:English Edition，2011，15(2):92-95．

Improved VIE Rainfall Retrieval Algorithm Based on SAR Measurements

ZHENG He， XIE Ya-nan， WAN Zhi-long， LIU Wen-yuan
(School of Communication and Information Engineering，Shanghai University，Shanghai 200072，China)

P 435

A

1007-2861(2012)05-0464-06

10．3969/j．issn．1007-2861．2012．05．005

2011-11-09

国家自然科学基金资助项目(61071185);上海市重点学科建设资助项目(S30108);上海市科委重点实验室资助项目(08DZ2231100);上海市科委科技攻关计划资助项目(10511501702)

谢亚楠(1962～)，男，研究员，博士生导师，博士，研究方向为微波遥感、电磁散射、射频电路等．E-mail:yxie@shu．edu．cn