基于机会维修模型的风电机组优化维修

赵洪山，鄢盛腾，刘景青

（华北电力大学，河北保定 071003）

风电机组一般安装在偏远的户外，运行环境恶劣，故障频繁发生。机组一旦发生故障，维修人员与维修设备到达故障现场，需要较长的时间和运输成本。据欧洲风电协会统计，风力发电机组每kW·h的运行检修费用占总生产成本的15%～25%[1]。目前风电场通常采取计划检修与事后维修方式。

风电机组是由叶片、齿轮箱、发电机、主轴承、电气系统、偏航系统、液压系统、机舱、塔架等部件组成的多部件复杂系统。对于复杂系统的维修，将其看成一个整体，用单部件维修策略确定的维修决策，已不能满足系统对维修费用最小化的要求，而必须考虑系统中不同部件的不同失效率、维修费用以及部件之间在维修方面存在的相关性[2-3]。在适合复杂系统的维修策略中，机会维修策略是研究较多的一种。所谓机会维修策略是指在对一个部件进行维修的同时对其他也达到维修要求的部件一起进行维修，这样分摊了系统的拆装、调试等高额固定维修费用，达到节约维修费用的目的。文献[4-8]考虑了状态和风险的各种电力设备的维修策略。

本文将机会维修考虑到预防维修和故障维修中，当一个部件需要维修时，对其他部件超过机会维修阀值的一起进行维修，从而节省了固定维修成本。通过仿真分析，机会维修策略比传统的役龄维修策略更加节省成本，从而验证了机会维修的科学性。

1 机会维修的基本原理

系统由N个不同部件组成，每个部件的失效率和维修费用都不一样，且每个部件的维修只在3种情况下发生，如图1所示。本文采用多部件维修策略中考虑了机会维修的情况，根据此维修策略优化系统各部件最优的机会维修役龄W和预防性维修役龄T，使系统的平均维修成本率最小。

对于机会维修，如图1所示，当部件的役龄在（0，Wi）之间时，如发生故障就进行故障更换；当部件的役龄在（Wi，Ti）之间时，如发生故障进行故障更换，或者如有其他部件因故障或达到预防性维修役龄而更换时进行机会更换；当部件的役龄达到Ti时，进行预防性更换。

图1 机会维修策略Fig.1 Opportunistic maintenance strategy

由于风机系统的复杂性，为了便于机会维修建模，做了如下假设：

1）风机系统中各部件故障率随时间的增加而增加。

2）风机系统中的各部件的故障率分布互相独立，且在机会维修策略中，只考虑部件之间的经济相关性，不考虑故障相关性。

3）风机系统中任意部件的故障更换或预防性更换都要求风机停机。

4）风机部件因故障导致的故障更换费用远远大于预防性更换费用。

2 风机关键部件的机会维修模型

2.1 风机关键部件概率密度函数

考虑一个1.5 MW的风机，其主要由齿轮箱、主轴承、发电机、叶片4个部件组成，且这4个部件的故障时间服从威布尔分布

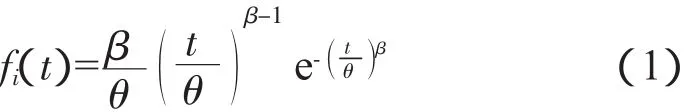
式中，fi（t）为威布尔函数；θ为特征寿命参数，天；β为形状参数。

2.2 风机关键部件的机会维修概率密度函数的确定

根据更新过程理论可知，当一个部件经过一定的周期或更换次数后，它的更换率就会接近一个常数，为部件更换期望周期的倒数。而且根据图1的机会维修策略可知，部件期望的更换率λi由3部分组成：部件役龄在（0，Ti）时的故障更换率λfi,部件役龄在（Wi，Ti）时的机会更换率λoi，部件役龄达到Ti时的预防性更换率λpi。因此

式中，λfi=Pi{f}·λi；λoi=Pi{o}·λi；λpi=Pi{p}·λi；Ei[T]为部件i的期望寿命；Pi{f}为部件进行故障更换的概率；Pi{o}为部件进行机会更换的概率；Pi{p}为部件进行预防性更换的概率。

由于部件i的机会更换是由任意其他部件的故障更换或预防性更换引起的，因此，引起部件i产生机会维修有2种可能：任意其他部件的故障更换率λfi和预防性更换率λpi。从可靠性角度来看，可以将这2种更换率看成是串联的，可以近似地将部件的机会更换概率密度函数看成如下的指数分布函数，即

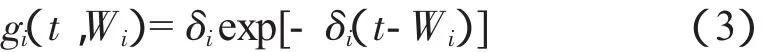
式中，gi（t，Wi）为机会更换概率密度函数；δi=为风电机组系统中关键部件的个数。

2.3 风机关键部件更换概率

风机各部件在1个更换周期内，部件i会进行3种更换策略：故障更换，机会更换和预防性更换，根据图1的机会维修策略可知它们的概率分别为

2.4 机会维修策略优化模型

在风电机组每个部件一个更换周期内，部件i的维修费用由更换费用和停机损失费用等组成，风机系统每次停机都有固定的维修费用，因为机会维修是在停机的基础上发生的，因此机会维修不包括系统的固定维修费用。

部件i的一个更换周期内的期望费用可以表示为

式中，C0为固定的维修费用；Ci1为部件i的故障更换费用；Ci2为部件i的预防性更换费用。

部件i的1个更换周期内的期望寿命可以表示为

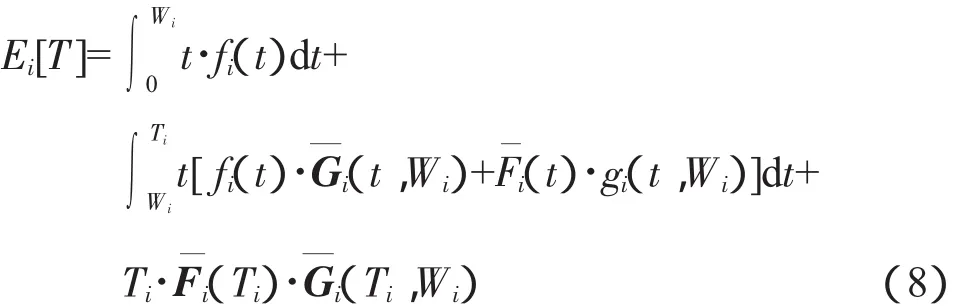
由上述分析，建立如下优化模型，优化风机各关键部件的机会维修役龄和预防性维修役龄使其平均费用率最小。

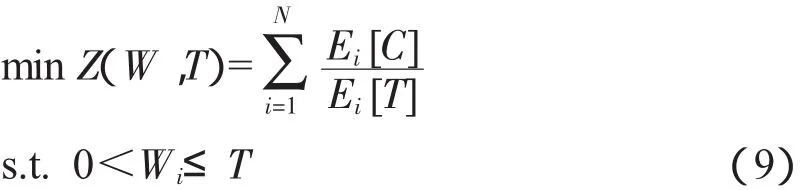
式中，Z（W，T）为风机平均费用率，￥/天。

3 风机机会维修的数值计算

本文所建立的机会维修模型是多变量，非线性的优化问题。由于目标函数很难推导出梯度和Hessian矩阵，所以无法对其应用牛顿法或内点法来进行寻优，因此，采取下面两步来进行寻优：第一步，求出已知优化参数情况下的目标函数值；第二步，在约束条件下，通过改变要优化的参数使目标函数最小，这里采用循环坐标法 (cyclic coordinate search)来达到优化目标。

首先，求出给定风机关键部件的机会维修役龄Wi和预防性维修役龄Ti时的风机平均费用率Z（W，T）。而要求解 Z（W，T），必须知道风机关键部件的机会更换率δi、故障更换率Pi{f}、机会更换率Pi{o}、预防性更换率Pi{p}和期望寿命Ei[T]的值，而根据式（2）、式（3）可知，确定 δi必须知道 Pi{f}、Pi{o}、Pi{p}、Ei[T]，根据式（4）、式（5）、式（6）、式（8）可知，确定 Pi{f}、Pi{o}、Pi{p}、Ei[T]必须知道 δi，这种互为前提的存在，必须先预估δi的值，然后进行迭代求解，其求解流程图如图2所示。

其次，通过优化风机关键部件的机会维修役龄Wi和预防性维修役龄Ti使目标函数值最小，采用循环坐标法来达到优化目标。该方法的主要原则是进行多变量优化时，搜索其中一个变量的同时保持其他变量为常数，且对其中一个变量的搜索采用黄金分割法来使目标函数最小。通过循环对每个变量都采用黄金分割法，最终使目标函数值达到最小。

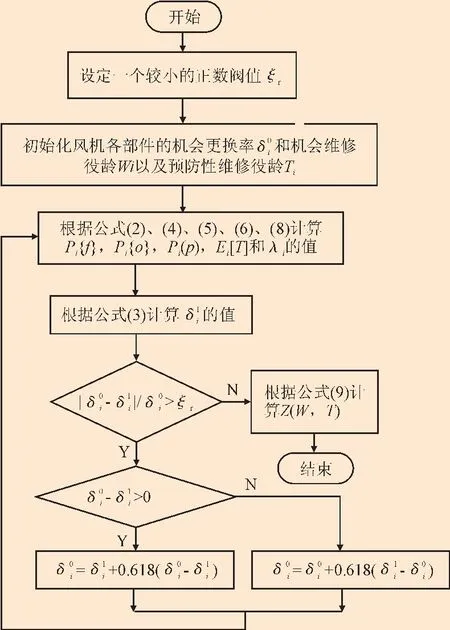
图2 求解Z（W，T）的流程图Fig.2 Solution of procedure of Z（W，T）

4 仿真分析

4.1 风机参数

对于一个1.5 MW的风机，其主要由齿轮箱、主轴承、发电机、叶片4个部件组成，且这4个部件的故障时间服从威布尔分布，表1给出了威布尔分布参数，表2给出了风机关键部件的更换费用[9]。

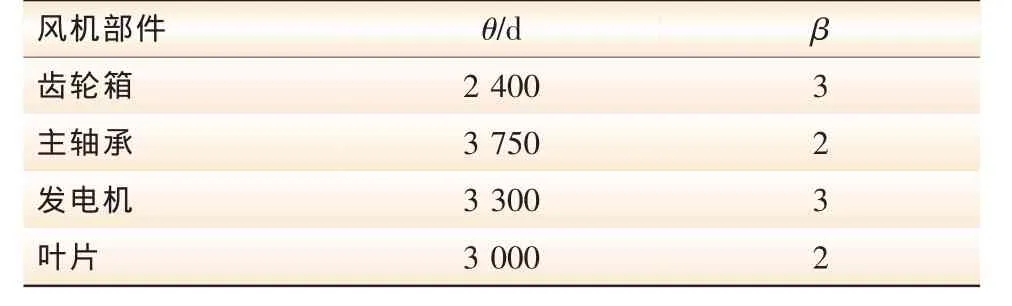
表1 风机关键部件的威布尔分布参数Tab.1 Weibull distribution parameters for major components of wind turbine

4.2 风机系统役龄维修策略结果

当采用役龄维修策略时[10]，优化风机关键部件的预防性更换役龄T使其平均维修费用率最小，表3显示了风机关键部件的役龄维修策略的优化结果。

表2 风机关键部件的更换费用Tab.2 Replacement costs for major components of wind turbine

表3 役龄维修策略优化结果Tab.3 Optimization results of age maintenance strategy

4.3 风机系统机会维修仿真结果

将表1、表2的数据带入上述机会维修模型中优化风电机组的各个部件的W和T，使目标函数达到最小。

当取初值W=600，T=3 000（初始值设置一）和初值为W=300，T=6 000（初始值设置二）时，机会维修的优化结果是一样的，见表4。其迭代过程和次数见图3。

表4 机会维修优化结果Tab.4 Optimization results of opportunistic maintenance

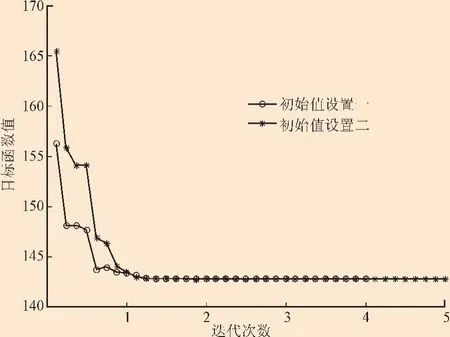
图3 初始值不同时的迭代结果Fig.3 Iterative results of different initial values

4.4 结果对比分析

由表3和表4结果对比可知，风机采用机会维修策略比役龄维修策略的维修费用率低21.688 7。在机会维修策略下，如果齿轮箱运行时间不多于1490 d，则进行故障更换，如果运行时间达到1490 d，则进行预防性更换，在上述2种齿轮箱更换情况下，如果主轴承的运行时间在（1 301，4 000），则进行更换，如果发电机的运行时间在（1 514，2 984），则进行更换，如果叶片的运行时间在（961，270 5），则进行更换，对于风机的其他部件也是如此分析。而在役龄维修策略下，部件的运行时间未达到T就进行故障更换，达到T就进行预防性更换。

机会维修策略是在维修一个部件的时候考虑另一部件是否达到维修要求，从而考虑一起维修，这样节约了固定维修成本，而役龄维修策略是对单部件的维修，对每个部件的每次维修都会产生固定维修成本，所以机会维修策略比役龄维修策略更加科学。

5 结语

由于风电机组的维修费用占风机运行总费用很大比例，所以研究风机维修很有意义。本文研究了机会维修策略，其优势在于各个部件有机会一起维修，节省了停机费用。通过仿真分析验证了机会维修的科学性，机会维修的期望费用要比役龄维修的期望费用要少，所以从长远角度上说，机会维修费用要少，从而节省了风机运行总费用，对风机维护有指导价值。

[1]BRAAM，RADEMAKERS L，VERBRUGGEN T W．CONMOW:ConditionMonitoring for Offshore Wind Farms[C]．ECN-RX-03-036.Petten，June 2003．

[2] 左洪福，蔡景，王华伟．维修决策理论与方法[M]．北京:航空工业出版社，2008．

[3] 刘华鹏．基于威布尔的风机齿轮箱元件最优更换时间[J]．电网与清洁能源，2011，27（4）:62-65．LIU Hua-peng．Optimal replacing intervals of wind turbine gearboxes elements based on weibull distribution[J]．Power System and Clean Energy，2011，27（4）:62-65（in Chinese）．

[4] 张宏．兼顾可靠性和经济性的电力设备最优状态维修策略[J]．电力科学与工程，2006，28（2）:8-13．ZHANG Hong．Optimal scheduling of condition-based maintenance for electric equipment considering reliability and economy[J]．Electric Power Science and Engineering，2006，28（2）:8-13（in Chinese）．

[5] 张燕．考虑备用成本的含风电场短期经济调度[J]．电力科学与工程，2011，27（4）:6-12．ZHANG Yan．Short-term economic dispatch considering spinning reserve costs for wind power integrated systems[J]．Electric Power Science and Engineering，2011，27（4）:6-12（in Chinese）．

[6] 谢荣斌．建立变电设备状态估计的智能信息平台[J]．南方电网技术，2009（3）:211-213．XIE Rong-bin．The platform of intellectual information based on electric equipment state assessment[J]．Southern Power System Technology，2009（3）:211-213（in Chinese）．

[7] 林金洪．基于气候因素的配电网络维修风险管理[J]．南方电网技术，2010，4（5）:92-95．LIN Jin-hong．Maintenance risk management of distribution network based on climatic factors[J]．Southern Power System Technology，2010，4（5）:92-95（in Chinese）．

[8]郭丽娟．基于风险的输变电设备状态检修实用技术体系[J]．南方电网技术，2011（5）:69-73．GUO Li-juan．A practical technology system for risk-based maintenance of transmission and transformation facilities[J]．Southern Power System Technology，2011（5）:69-73（in Chinese）．

[9] TIAN Zhi-gang，JIN Tong-dan，WU Bai-rong，et al．Condition based maintenance optimization for wind power generation systems under continuous monitoring[J]．Renewable Energy，2011（36）:1502-1509．

[10]RADOUANE LAGGOUNE，ALAA CHATEAUNEUF，DJAMIL AISSANI．Opportunisticpolicyforoptimalpreventive maintenance of a multi-component system in continuous operating units[J]．Computers and Chemical Engineering，2009（33）:1499-1510．