基于舰船噪声小波包重构子带权重系数的确定方法＊

张 洋 李训诰 林一品

（1.海军潜艇学院 青岛 266000）（2.东海舰队司令部 宁波 315000）

1 引言

潜艇及水面舰艇在海战中，先敌发现并有效地对敌进行水声对抗，先敌使用武器攻击，正确有效地进行目标特征提取是克敌制胜的前提，也是海军各型潜艇和水面舰艇急需解决的关键技术。然而，舰船辐射噪声的复杂性和多样性，同类目标信号的离散性和不同类目标信号之间的相似性，海洋环境和本艇各种噪声的污染，水声信道的特殊性，使得舰船噪声的特征提取一直是水声信号处理的一个难题。

提取舰船噪声特征，进行噪声源的识别与定位，是降低舰船辐射噪声强度的基础，因而舰船的噪声源识别已成为人们关注的焦点问题之一。传统的噪声源识别方法在时域处理范畴，主要有分部运转、时力分析、辐射效率测定和相关分析等方法；在频域处理范畴主要有谱分析方法、相关分析方法和偏相干分析方法。

小波包变换对信号具有任意的多尺度分解形式。它通过小波包分解将频带多层次划分，并能够根据被分析信号的特征自适应地选择频带。不同的小波包基具有不同的性质，反映不同的信号特性，能提供其他变换所不能提供的信号的重要特征。本文提出了一种基于小波包分解与能量特征提取的分析方法。

2 基于小波包的噪声分解与重构

小波包分析能够为信号提供一种更加精细的分析方法。它将频带进行多层次划分，对多分辨分析没有细分的高频部分进行进一步分解，并能够根据被分析信号的频率，自适应地选择相应频带，使之与信号频谱相匹配，从而提高时频分辨力，因此小波包具有更广泛的应用价值。

2.1 小波包分解与重构的基本原理

式中：g（k）＝（－1）kh（1－k）即两系数也具有正交关系。

在多分辨分析中，φ（t）和ψ（t）满足双尺度方程：

由以上各式构造的序列 ｛wn（t）｝n∈z＋为 由基函数 w0（t）＝φ（t）所确定的小波包，它是包括尺度函数 w0（t）和小波母函数w1（t）在内的一个具有一定联系的函数的集合。

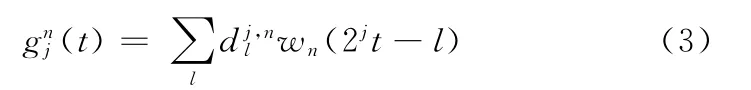
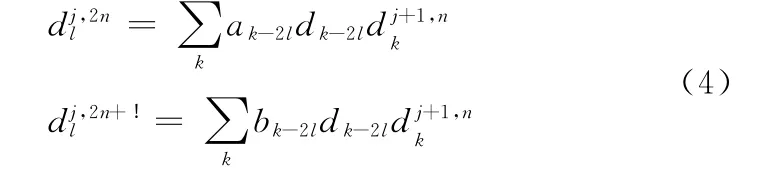
小波包的分解示意如图1所示。

图1 小波包分解示意图

2.2 小波包的构建

根据小波包函数空间正交剖分理论，设噪声信号采样率为fs，小波包第j层的第n个子带的中心频率和带宽为

依据式（6）确定各子代的中心频率及带宽，将其与适当的频率尺度进行对照，即可得到小波包分解的结构。本文采用的舰船噪声信号样本采样率为Fs＝44.1kHz。采用db6小波，以最大小波包分解层数N＝8对分解。本文采用的频率尺度为Mel频率尺度，线性频率f与Mel频率之间的转换公式为

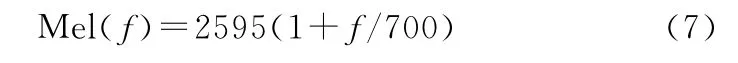
图2 Mel小波包结构图

图2为使用24个叶节点构建的小波包结构图以及各子带所对应的中心频率，该小波包在低频部分较高频部分划分更为精细，较好的模拟了人耳基底膜对信号的非线性处理过程，本文将使用此小波包对舰船噪声进行分解和重构。

3 小波包重构子带权重系数的确定

为了综合利用各Bark子带的信息，需要在重构时给于各子带一权重系数。本文以小波包系数能量百分比作为子带权重系数。

小波包变换是一种线性变换，满足能量守恒定理，小波包系数具有能量的量纲，可用作类似能量的分析。设Wi，j表示的子带是经过N层小波包分解后的第i层第j个叶节点，其中0≤j≤2N－1，cj，k为这个节点的小波包分解系数，k＝1，2，...，n，其中n为此叶节点的系数总数，本文取n＝24。其系数能量可通过随机信号能量计算方法计算：

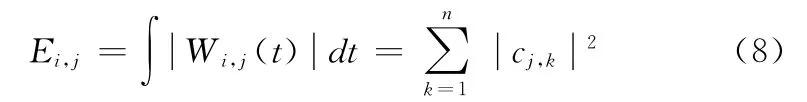
则第j个叶节点所分配的权系数为

Bark子带系数能量特征向量为［η1，η2，η3，...，ηn］，即小波包重构所需子带权重系数向量。

4 实验结果分析

实验采用大量不同水文气象条件下实录的采样率为Fs＝44.1kHz的舰船噪声信号作为样本，按照如下的实验步骤：

1）对舰船噪声信号样本进行滤波，选择合适的频带宽度，同时降低采样率，以降低运算量提高运算速度；

2）对滤波后的噪声使用分解结构如图4的Bark小波包进行分解，提取子带能量，构建子带系数能量特征向量［η1，η2，η3，...，ηn］，并以此作为权重系数。

3）对每个子带的系数能量向量进行权重为ηnj∈［0，1］的加权，按照式（10）进行重构：

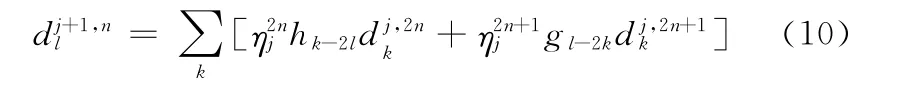
实验流程如图3所示：

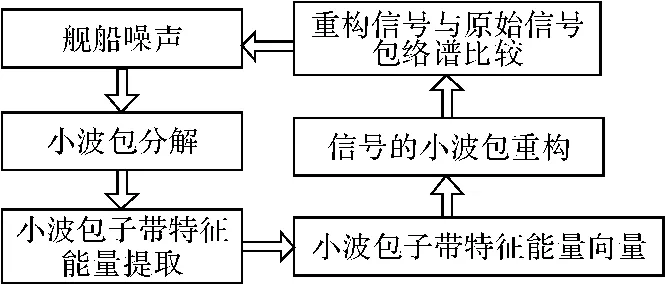
图3 Mel小波包结构图

图4为1号舰船目标重构噪声与原始噪声的比较。在时域，重构信号较原始信号去除了一些冗余成分，“瘦身”许多；在频域，主要特征信息的频段得到了加强；从重构信号的包络谱中能看出基频与其各次谐波，以及本艇自噪声，而这些信息在原始信号包络谱中是不易看出的。

图5为2号舰船目标重构噪声与原始噪声的比较。重构噪声信号的包络谱线谱干净、清晰，所表达的基频及谐波成分一目了然，在听测时也发现重构噪声中节奏更加明显。

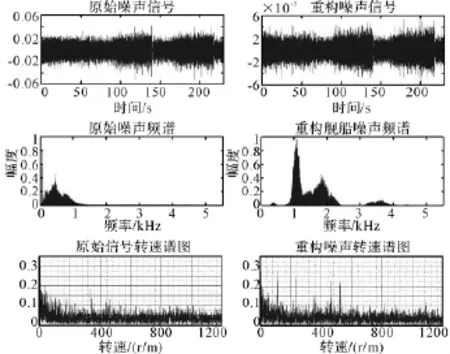
图4 1号目标原始噪声与重构噪声包络谱对比图

图5 2号目标原始噪声与重构噪声包络谱对比图

综合以上分析，利用听觉模型，模拟人耳基底膜对信号的频率分解特性，对舰船噪声使用Bark小波包分解，并以小波系数能量百分比为权重系数进行重构的信号，较原始信号特征更为明显，有更强的类别可分性。

［1］曾芸，武和雷.基于小波包的频带能量的特征提取及智能诊断［J］.计算技术与自动化，2008（12）：115－118.

［2］谷小红，张光新.小波包分解与能量特征提取相结合的水管泄露位置的确定［J］.四川大学学报，2001（11）：145－149.

［3］谢光军，等.Matlab7辅助信号处理技术与应用［M］.北京：电子工业出版社，2005.

［4］Hrvoje Sikic，Tight frame wavelets and the dimension function［J］.Wavelets and Applications－Lecture Notes，2002（1）：79－486.

［5］王品，小波变换用于舰船轴射噪声调制信息检测［J］.哈尔滨工程大学学报，2004，25（1）：53－57.

［6］Simon Tueke，Auditory analysis of sonar signals［R］.PhD.Transefr RePort，2001.

［7］王大凯，彭进业.小波分析在信号处理中的应用［M］.北京：电子工业大学出版社，2006.

［8］于帆，张硕.一种基于小波基函数的电网故障测距方法研究［J］.计算机与数字工程，2012（8）.

［9］Fu Tai Wang，Jenny Chih Yu Lee，Shun Hsyung Chang，et al.Signal Detection in Underwater Sound by Dual－Tree Discrete Wavelet Transform，1－4244－0635－8／07，IEEE，2007.

［10］Hrvoje Sikic，Tight frame wavelets and the dimension function，Wavelets and Applications－Lecture Notes，vol.1，2002：79－486.

［11］张静远，张冰.基于小波变换的特征提取方法分析［J］.信号处理，2000，16（2）：155－162.