电子装备故障预测方法研究*
2012-10-16刘爱军金国庆
刘爱军 金国庆
(海军工程大学 武汉 430033)
1 引言
由于电子装备日趋复杂,很难了解系统的行为特征,实际中还需利用电子装备系统的历史信息和动态信息,实现对系统未来的运行状态和发展趋势做出估计,防止灾难性故障的发生,因此迫切需要有效的预测模型来监督电子系统劣化的变化趋势。状态预测是比故障诊断更高级的监测技术,是一门涉及多学科综合的新兴边缘学科。它以当前系统的状态为起点,结合被预测对象的近期监测数据、环境条件及历史数据,通过相应的预测算法对被监测数据进行分析,对系统未来时刻的运行状态进行预测、分析与决策,以便及时在故障发生之前采取有效措施保证系统的顺利运行。电子装备系统的状态预测比故障诊断具有更重要的实际应用价值:它可以实现对故障的提前预警,以便及早采取相应的措施,为系统后续的正常运行争取时间,其次也增加了系统的故障预测能力,对装备在未来时刻中可能出现的故障进行预测,以便进行预防维修。
20世纪90年代后,随着人工智能技术的发展,模糊理论、神经网络、小波技术以及支持向量机都相继应用于该领域并取得了良好的效果。本文主要引入最新的故障预测方法。
2 故障预测的流程

图1 故障预测流程图
故障预测的流程如图1所示。首先根据电路元器件的失效机理,设定其性能参数随时间的变化趋势;接着根据此趋势设置电路参数进行电路仿真;然后选择适当的监测信号,根据监测信号与特征参数之间的关系,选择适当的特征提取方法计算特征参数;重复上述过程,监测一段时间内若干时刻点特征参数值,作为预测的训练样本;利用预测算法进行建模,得到特征参数的变化趋势并对未来时刻进行预测;最后对预测结果进行分析,实现故障预测与剩余寿命估计。
3 电子装备的故障预测方法
3.1 灰色模型预测方法
3.1.1 灰色系统理论
灰色理论认为任何随机过程都是在一定幅值范围和一定时区变化的灰色量,并把随机过程看作灰色过程。灰色系统是通过对原始数据的整理来寻求其变化规律即称为灰色序列生成。该理论认为尽管客观系统数据表现离乱,但它总是有整体功能的,因此必然蕴含某种内在规律,关键在于如何选择适当的方式去挖掘和利用它。一切灰色序列都能通过某种生成弱化其随机性,显现其规律性。灰色系统在建模时常用以下几种序列缓冲算子对原始数据进行生成处理,使生成的数据序列具有一定规律。
1)累加生成
累加生成是使灰色过程由灰变白的一种方法,通过数据累加来弱化数据信息的随机性,显示出数据中蕴涵的规律,从而建立系统预测模型。对于非负序列,累加生成次数越多,数列的随机性就弱化得越多,在GM模型中一般只对数据作一次累加生成。

称D为X(0)的一次累加生成算子,记为1-AGO(Accumulating Generation Operation,AGO),称r阶算子Dr为X(0)的r次累加生成算子r-AGO,习惯上记为

其中,
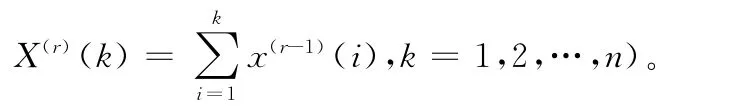
非负序列经过上述累加生成后都会减少随机性,呈现出近似的指数增长规律。原始序列越光滑,生成后的指数规律也越明显。
2)累减生成
累减生成是在获取增量信息时常用的生成,与累加生成是一对互逆的序列算子,设有原始序列 X(0)=(x(0)(i),i=1,…,n),D 为序列算子
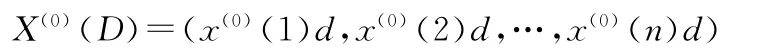
其中 X(0)(k)=x(0)(k)-x(0)(k-1),k=1,2,…,n。
称D为X(0)的一次累加生成算子,称r阶算子Dr为X(0)的r次累加生成算子r-AGO,习惯上记为
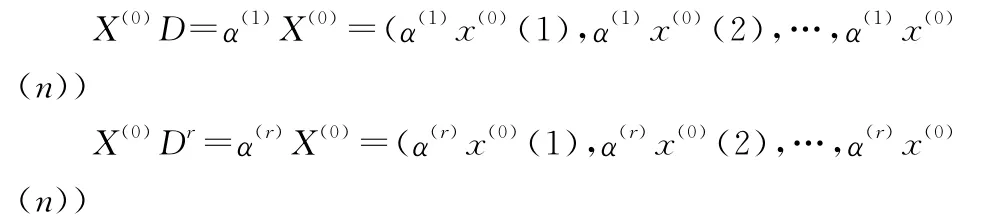
其中,α(r)X(0)(k)=α(r-1)x(0)(k)-α(r-1)x(0)(k-1),k=1,2,…,n
3)均值生成
由于一些不可预知的外界因素有时会导致数据序列出现空缺,或数据虽完整但某个点的数据为明显异常数据,删除该数据也会导致原有数据序列出现空缺,均值生成成为填补空缺数据的有效方法。设序列x=(x(1),x(2),…,x(n)),若x*(k)=0.5x(k)+0.5x(k-l)则称x*(k)为紧邻信息的均值生成,由紧邻均值生成数构成的序列称为紧邻均值生成序列。
3.1.2 灰色模型的建立
设有原始数列X(0)=(x(0)(i),i=1,…,n),对序列做一次累加生成:
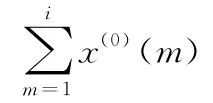

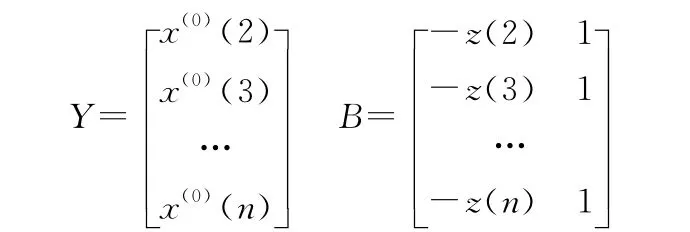
灰色模型方程的解为

则模型的还原值为

3.2 SVR预测方法
支持向量回归(Support Vector Regression,SVR)是支持向量机(SVM)用于回归预测问题时的一种技术。通过回归训练,实现函数拟合功能,并在此拟合函数的基础上实现外推预测 。
1)LS-SVM 算法原理
最小二乘支持向量机(Least Squares Support Vector Machines,LS-SVM)回 归 预 测 是 SVM 用 于 回 归 预 测(SVR)的一种算法,它继承了SVM众多优点,已被用于时间序列的预测中。其基本思想是通过非线性映射将输入向量X映射到高维特征 Hilbert空间,并在这个空间进行线性回归,通过一个线性约束的二次规划问题得到全局最优解。
SVM回归函数表达式为

其中,f(x)为预测的输出;φ(·)表示非线性函数;x为输入;w为权值;wT为w 的转置;b为偏差;Rn是N 维实数空间;R为实数。
基于Support Vector的最优回归函数是指满足结构风险最小化原理,极小化上式将不等式约束转化成等式约束,变为

其中,ei为误差;γ为常数;xi为训练样本输入X=(x1,…,xi,…,xn)中第i个分量;yi为输出样本Y=(y1,…,yi,…,yn)中第i个分量。
依据对偶定理,建立拉格朗日(Lagrange)方程,引入Lagrange算子αi,得到:

根据 Karush-Kuhn-Tucker定理,最终可得LS-SVM 回归函数如式所示:

空间映射过程是通过核函数K(x,y)=φ(x)·φ(y)实现的,核函数是满足Mercer条件的内积核函数,常用的有线性核函数、多项式核函数、径向基核函数、Sigmoid核函数等。
2)LS-SVM算法主要参数
利用LS-SVM进行预测的函数主要有回归训练trainlssvm函数和预测simlssvm函数。函数的主要输入参数为训练样本、预测样本、核函数kernel、调整参数gam和核参数sig2。
3.3 BP神经网络预测方法
反 向 传 播 神 经 网 络 (Back-Propagation Neural Network,BPNN)是1986年由Rumelhant和Mcllelland提出的一种多层网络的“逆推”学习算法,它是目前应用最为广泛和成功的神经网络之一,已被广泛的应用于函数逼近,模式识别、分类和数据压缩等领域。
1)前馈神经网络
前馈神经网络通常可分为不同的层,第i层的输入只与第i-1层的输出相连,输入输出节点由于可以与外界相连,直接受环境的影响,成为可见层,而其他的中间层则成为隐层。
2)反向传播算法
反向传播算法的主要思想是从后向前(反向)逐层传播输出层的误差,以间接算出隐层误差。BP算法的学习过程由正向传播和反相传播两部分组成。在正向传播过程中,输入模式从输入层经隐层神经元的处理后,传向输出层,每一层神经元的状态只影响下一层神经元状态。如果在输出层得不到期望的输出,则转入反向传播,此时误差信号从输出层逐层向输入层传播并沿途调整各层间连接权值和域值,以使误差不断减小,直到达到精度要求。
3)BP神经网络主要参数及选取
在进行BP神经网络设计时,主要的参数有网络的层数、每层的神经元个数、初始值、学习速率及期望误差等。
(1)隐层数及其神经元个数设计
理论上已经证明一个S型隐层加上一个线性输出层网络,可以逼近任何有理函数。所以最常用的BP神经网络一般为3层,即输入层,1个隐层(S型)、输出层(线性)。增加隐层数主要是为了降低误差,使精度更高,但层数的增加也使网络变得复杂,增加网络权值的训练时间。增加每层神经元的个数的目的也是为了提高精度,而且相比增加隐层数其训练效果更容易观察和调整。所以一般都是在满足一定的误差精度的条件下尽量增加每层神经元的个数,在增加个数仍不能满足精度要求时,才考虑增加隐层数。
神经元个数的确定一般根据经验确定。其中一种确定方法如式所示

(2)初始权值的选取
一般希望经过初始加权后每个神经元的输出值都接近于零,保证每个神经元的权值都能够在S型激活函数变化最大处进行调节,所以,初始值一般取值在-1~1之间。
(3)学习速率的选取
学习速率决定每一次循环训练中所产生的权值变化量。为了保证系统的稳定性,学习速率一般选择在0.01~0.8之间。本文中采用可以减小寻找学习速率的训练次数以及训练时间的自适应学习速率方法。
(4)期望误差的选取
在训练过程中,期望误差值的大小直接决定了训练的精度及训练时间,需根据误差精度要求及训练性能综合考虑确定。
4 结语
本文介绍了电子装备系统故障预测的概念,以及故障预测的流程,并对预测的方法进行了研究。其中展开对灰色系统理论进行研究并建立了故障预测的灰色模型方法;以及建立了最小二乘支持向量机(LS-SVM)回归预测算法和反向传播神经网络预测方法。三种故障预测方法的建立为后续电子装备的故障预测建立了理论基础。
[1]曹立军,杜秀菊,秦俊奇,等.复杂装备的故障预测技术[J].飞航导弹,2004,20:23-27.
[2]朱冰静,朱宪辰.预测原理与方法[M].上海:上海交通大学出版社,1991:3-8.
[3]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987:1-25.
[4]江田汗,束炯.基于LS-SVM 的混沌时间序列的多步预测[J].控制与决策,2006,21:77-80.
[5]吴珂,杨丽霞,王海瑞.量子神经网络在电力谐波检测中的应用[J].计算机与数字工程,2012(02).
[6]黄晶晶,熊才权.粗糙集-神经网络在作战效能评估中的应用[J].计算机与数字工程,2011(05).
[7]闻新,周露,王丹力.MATLAB神经网络应用设计[M].北京:科技出版社,2000:207-232.
