水下拖体和拖缆运动模型研究探讨*
2012-10-16曹帅辉
曹帅辉
(中国船舶重工集团公司第七一〇研究所 宜昌 443003)
1 引言
近年来,随着海洋工程的发展,水下拖曳系统作为一种水下探测平台得到了广泛关注,如海洋环境勘测、海洋石油开发等。一般来讲,此类拖曳系统可简化为由水面拖船、拖缆、水下拖体组成的多体系统,如图1所示,其中,水下拖体作为搭载各种探测仪器的主体,在设计时需要研究其运动特性,并采取相应的控制手段确保其运动稳定性。

图1 水下拖曳系统示意图
水下拖体在运动时所受的干扰主要由流场干扰和拖缆干扰两部分组成。在海洋工程中,由于拖曳深度较深,通常只研究拖缆干扰。拖缆干扰主要由流场干扰、自身振动干扰和拖船干扰几部分组成,其中,拖船干扰通常被认为是主要部分。拖船在波浪上的不规则运动常会通过拖缆传递到拖体上,从而对拖体产生不稳定扰动,扰动程度取决于作业海况和拖船对波浪的响应程度,这种扰动常常会导致拖体中的仪器超出正常工作范围。因此,迫切需要建立拖船、拖缆和拖体的系统运动模型,研究拖船干扰对拖体运动的影响,为水下拖曳系统的研制提供基础。
针对上述情况,本文将结合水下拖曳系统的工程实际,建立由拖船、拖缆和拖体组成的水下拖曳系统的运动模型,并进行仿真研究,研究拖船干扰对拖体运动的影响。
2 水下拖体运动模型
记水下拖体在地面惯性坐标系中的广义位置向量为η=[x y z φ θ φ]T,其中,x,y,z为水下拖体浮心处的坐标,φ,θ,φ为水下发射平台的俯仰角、偏航角和横滚角;同时记水下拖体在其随体坐标系中的广义速度向量为v=[vxvyvzωxωyωz]T。
根据Newton-Euler方法,将体坐标系下水下拖体的运动方程写成矢量形式有:

式中,M=MA+MB为广义质量矩阵,MA为附加质量矩阵,MB为水下拖体的质量矩阵,有:


C=CA+CB为Coriolis矩阵,CA为附加流体的Coriolis矩阵,CB为水下拖体的Coriolis矩阵,有:



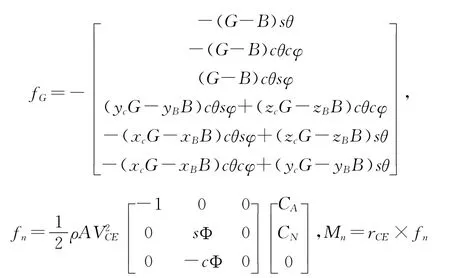
其中,VCE为水下拖体压力中心的速度;Φ为旋转角,定义为:Φ=tan-1(-vCE/wCE);rCE为体坐标系原点到水下拖体压力中心的距离矢量;CA为水下拖体在纵平面内的阻力系数,CN水下拖体在纵平面内的升力系数,CA和CN可通过流体动力参数试验获得。
另外,拖缆对水下拖体的作用力fM由水下拖体和拖缆之间的边界条件决定。
3 拖缆运动模型
在本文的建模中,拖缆被假设成连续的细长圆柱状缆索,并将其看成完全绕性构件,忽略其剪应力和弯矩,沿拖缆轴向的应力只能为张力。


式中,


其中,d0为拖缆直径,w为单位长度拖缆在水中的重量,(ut,un,ub)为拖缆微元相对于水的运动速度,(vwet,vwen,vweb)为水流速度在拖缆局部坐标系中的分量,ct和cn为拖缆的切向和法向阻尼力系数。
4 边界条件
系统运动模型求解的边界条件即为拖缆的首端和自由端(系留点)的边界条件。
1)首端边界条件:

式中,下标bottom表示拖缆下端点,速度Vbottom为船在波浪等外界干扰下的速度。
2)自由端边界条件
(1)速度边界


(2)拉力边界
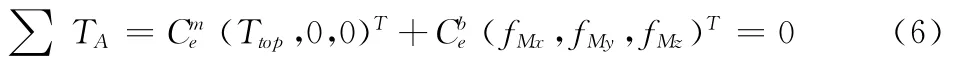
式中,(Ttop,0,0)T为拖缆自由端所受拉力在拖缆局部坐标系中的坐标矢量,fM=(fMx,fMy,fMz)T为拖体受拖缆拉力在其体坐标系中的坐标矢量。
联立方程(1)~(6)即得到水下拖曳系统的运动方程组,在给定初始运动条件的情况下,结合相应的数值算法,该系统的运动模型可以封闭求解。
5 仿真算例与结论
在上述系统模型下,对某直径为0.34m,长度为1.57m的拖体,在水面拖船拖曳下进行仿真,拖船速度6.28m/s,波高1m,波浪周期6s,波向与拖体呈45°夹角,拖体在水下的92m附近能实现稳定拖航,其仿真计算结果如图2。
由仿真结果可看出,当拖船受到波浪等外界因素干扰时,拖体的位置和姿态也随之改变,该运动模型建立可很好得反映了水下拖体受干扰情况下的运动状况,通过不同外界条件的仿真,可很好得评估整个拖曳系统的安全运动工况,为水下拖曳系统的研制及实海况试验提供参考。

图2 拖体在水中位置与姿态随时间的变化曲线
[1]Ablow C M,Schechter S.Numerical simulation of undersea cable dynamics[J].Ocean Engineering.1983,10(6):443-457.
[2]Fossen T I.Guidance and control of ocean vehicles[M].UK:John Wiley&Sons Ltd.,1994.
[3]Hearn,G.H.,Thomas,D.O..The influence of practical time integration schemes on dynamic mooring line analysis.Proc.of the 23th Offshore Technology Conference OTC Paper 6604,1991,397-409.
[4]Jason Evans,Meyer Nahon.Dynamics modeling and performance evaluation of an autonomous underwater vehicle[J].O-cean Engineering,2004,31:1835-1858.
[5]Jiaming Wu,Allen T Chwang.A hydrodynamic model of a two-part underwater towed system[J].Ocean Engineering,2000,4(27):455-472.
[6]休斯顿,刘又午.多体系统动力学[M].天津:天津大学出版社,1991:1-103.
[7]刘乐华,罗金玲.水下锚系动基座发射系统动力学建模[J].舰船科学技术,2005,27(6):54-57.
[8]邵成,艾艳辉,代军.水下锚系导弹发射系统运动研究[J].兵工学报,2011(9).
[9]邵成,宋保维,李家旺,等.携带正浮力载荷AUV的载荷分离运动仿真研究[J].系统仿真学报,2008(9).
