基于时间序列分析的预测控制算法＊

张 同 李 伟 叶永安 阎 隽

（1.中国船舶重工集团公司第七二二研究所 武汉 430079）（2.73141部队司令部 南安 362301）（3.武汉东湖学院 武汉 430212）

1 引言

按照时间次序排列的一系列离散观测值称为一个时间序列，分析时间序列数据的统计方法被称为时间序列分析。传统的统计分析认为，观测是统计上相互独立的，而在时间序列分析中，观测的次序是很重要的，观测值都是相互关联，相互依赖的［1］。

时间序列理论通过引入线性系统的分析方法，寻找一个能完成将相关的时间序列输出化为不相关的独立数据转化模型，然后对独立的多次观测使用一些标准的统计方法，进行估计、预测和控制。

线性预测这一概念最早是维纳在1947年提出的，此后，线性预测应用于许多领域中。线性预测分析的基本概念是信号的抽样能够用过去若干个语音抽样的线性组合来逼近。通过建立高阶线性方程的方法来描述模型，预测系数就是线性组合中所用的加权系数。

2 插值和拟合

根据所给的函数表，求一个不高于n次的代数多项式

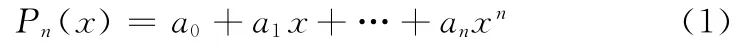
使得

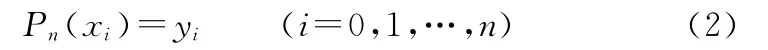
满足公式（2）的多项式（1）称为函数f（x）在节点xi（i＝0，1，…，n）上的n次插值多项式。求函数f（x）的n次插值多项式Pn（x）的几何意义，就是通过曲线y＝f（x）上的n＋1个点Mi（xi，yi）（i＝0，1，…，n），作一条n次代数曲线y＝Pn（x）近似代替曲线y＝f（x）。

3 预测控制算法

建立n阶多项式线性模型：

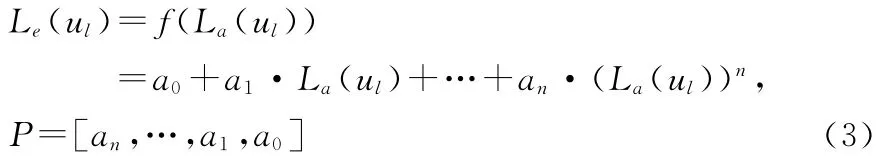
其中P为系数向量。在已知n次迭代过程中的La（ul）和Le（ul）的基础上对n＋1次迭代过程中的Le（ul）进行预测估计［4］。

图1 改进的Turbo码译码结构

线性模型可以是多项式线性模型，也可以是AR模型，建模的关键和难点并不在建立模型本身，因为建模本身是非常成熟的，预测的难点在于模型建立之后处理数据时所用到的误差补偿算法，即对预测结果进行控制［5］。针对采样点过少可能会导致预测出现偏差的问题，误差补偿算法需做到以下两点：

1）保证预测值与采样值具有相同的正负取值［6］。迭代译码本身就是通过外部信息值在分量译码之间的传递，使得外部信息值随着迭代次数的增加，分布和取值趋于稳定的过程。在少数情况下，外部信息值的波动，会影响线性预测模型的预测系数，进而出现不能反映变化趋势的预测点，应加以纠正。

2）需根据信道环境的不同，设定预测值与前一个采样值之间的差值阈值。高信噪比情况下，外部信息值的变化较为舒缓，应采用较小的差值阈值；低信噪比情况下，外部信息值的变化较为震荡，应根据采样点的差值情况，确定适当的差值阈值。阈值的选取应使得实际抽样和线性预测抽样之间差值的平方和达到最小，即进行最小均方误差的逼近［8～9］。

不同的预测算法和不同的信道环境下，误差补偿算法应为不同且自适应的。误差补偿算法选取不当会直接影响预测值的准确性。

4 改进的迭代译码过程

在有限次的迭代译码过程中，预测控制算法可以彼此叠加，形成基于一次、复次甚至多次预测的改进译码结构，从而缩短译码时延，提高译码效率，所加入的预测次数与误码率成正比关系［10］。

在串行译码结构中，预测模块的叠加在单通道中顺次进行，如图2所示。试验表明，多个预测模块之间的间隔有助于误码率性能的平稳。

图2 串行译码结构中的单、复次预测

在并行结构中，由于在两个通道中，分量译码器的译码过程是彼此独立不相关的，预测模块的叠加是在双通道中顺次进行的［11］，如图3所示。

图3 并行译码结构中的单、复次预测

5 仿真分析

5.1 外部信息对比分析

通过观察分量译码外部信息的变化，验证在迭代过程中加入预测控制模块的可行性。仿真试验采用并行译码结构，迭代次数为10次，分别对译码器2的外部信息进行单次和复次预测。

图4（a）～（d）为采用线性预测控制模块对第6～9次迭代过程中分量译码器2外部信息值的单次预测与传统分量译码器译码的外部信息值的比较；图4（e）和（f）分别是采用线性预测控制模块在一次译码中对第6次和第8次、第7次和第9次迭代过程中分量译码器2外部信息值的复次预测与传统分量译码器译码的外部信息值的比较。

仿真结果表明，单次预测时，外部信息值能够很好的回归，与传统译码具有相同的趋势；复次预测时，波动较大，但仍能有回归的趋势。线性预测控制模块得到的外部信息值的走势与传统译码相同，证明可以使用线性预测控制模块代替传统译码结构中的分量译码器。

图4 外部信息值的预测仿真

5.2 译码时延对比分析

引入线性预测控制模块的最终目的是减少迭代过程中的译码时延。在L（2）a（n＋1）（ul）未送入预测计算单元之前就能够计算出P值，为达到减少时延的最佳效果，在第n＋1次迭代过程中，分量译码器2的译码过程即可简化为对系数P 已知的多项式Le（ul）＝f（La（ul））的求解过程。

图5（a）～（e）分别为帧长1024、512、256、128、64时，分量译码器1的译码时延tdec1与P值运算单元的计算时间tpc的比较（表1列出具体数值）。当帧长为1024、512、256、128时，tdec1大于tpc，即在L（2）a（n＋1）（ul）未送入预测计算单元之前即可计算出P值。当帧长为64时，tdec1与tpc在一个动态范围之内。因此，对于短帧译码序列，线性预测控制模块并没有体现出较大的优势，帧长越长优势越明显。

表1 译码时延对比

图5 分量译码器1的译码时延与P值运算单元的计算时间的比较

［1］H.E.Gamal and A.R.Hammons.Analyzing the turbo decoder using the Gaussian approximation［C］／／Proc.ISIT’2000.Sorrento，Italy.June 2000：870－876.

［2］X.Liao，J.Ilow，and A.Al－Shaikhi.Trellis termination in turbo codes with full feedback RSC encoder［C］／／4th International Symposium on Turbo Codes and Related Topics，Apr，2006：504－510.

［3］Xiangyu Xue，Ke Wang，Zhao Xu.Parallel Decoding Structure of Turbo Code Based on Double Prediction Control ［C］／／WiCom2010.September，2010.

［4］孙增友，赵云鹏，李春前.一种基于 Matlab的Turbo码仿真技术的研究与实现 ［J］.东北电力大学学报，2007，27（6）：44－48.

［5］刘陈，吴成林.Turbo码并行译码算法的研究 ［J］.南京邮电学院学报（自然科学版），3，2002，22（1）：90－94.

［6］Zhao Xu，Ke Wang，Zhuo Li，et al.Iterative Decoding Structure Design of LPCA－Turbo ［C］／／The Second International Conference on Information and Computer Science，UK，May 21－25，2009.

［7］杜星玥，卢昱，陈立云.制导弹药飞行视景仿真系统的时间管理研究［J］.计算机与数字工程，2012（2）.

［8］肖东亮，石鸿凌，孙洪，等.一种改进的S－random随机交织器的设计 ［J］.电路与系统学报，8，2005，10（4）：23－27.

［9］J.Nonnenmacher，E.Biersack，D.Towsley.Parity－based loss recovery for reliable multicast transmission ［J］.IEEE／ACM Trans.Networking，Oct.1998，6（8）：349－361.

［10］J.Nonnenmacher，E.Biersack，D.Towsley.Parity－based loss recovery for reliable multicast transmission［J］.IEEE／ACM Trans.Networking，Oct.1998，6（8）：349－361.

［11］A.Al－Shaikhi，J.Ilow.Improved upper bound for erasure recovery in binary product codes［C］／／Proc.IEEE 16th International Symposium PIMRC’05，Sept.2005，2：1086－1090.