舰船运动姿态仿真与多层AR预报研究＊

王玉珍 姜礼平 肖 鹏

（海军工程大学 武汉 430033）

1 引言

舰船构成海上的主要战斗力，各种作战装备如弹炮装备、舰载机等均以舰船海上作战平台为依托。保障舰船航行的安全性，以确保舰船各项作业的顺利完成，是我国海军关注的重点。为此，国内诸多单位陆续开展了舰船运动姿态预报理论的研究［1～3］。

对舰船运动姿态预报的方法［4～5］主要有频域分析法和时域分析法两种，其中，频域分析法假设任何一种无趋势的时间序列都可以分解成若干不同频率的周期波动，从能量叠加角度进行时间序列分析与预报，该方法是一种非常有用的动态数据分析方法，但方法复杂，结果抽象，有一定的使用局限性；时域分析法认为事件的发展通常都具有一定的惯性，通过寻找序列的相关关系进行预报，其理论基础扎实，操作步骤规范，分析结果易于解释，是时间序列预报的主流方法。

2 舰船运动姿态仿真

舰船航行海情复杂，随机海风、海浪、洋流等因素均对舰船运动产生较大影响。本文在仿真随机风浪的基础上构建船舶运动姿态仿真模型。

2.1 随机风浪仿真

随机风浪的建模方法主要为波浪叠加法［6］和有理谱法。本文采用波浪叠加法进行海浪仿真。某一定点海浪在t时刻的振幅表达式如下：

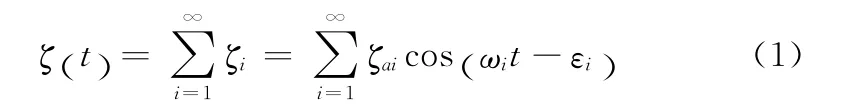
式中，ζai为单元规则波的振幅；ωi为单元规则波的圆频率；εi为单元规则波的相位，可在0～2π之间任意取值，且是等概率分布的。

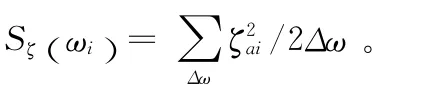
本文采用纽曼海浪谱进行分析，即：

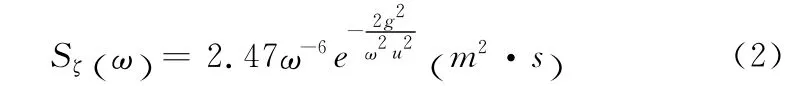
式中，u为平均风速，m／s；ω为波浪圆频率，m／s－1；g为重力加速度，9.81m／s2。

由此，海浪波倾角为：

综上，即可求得波倾角仿真规律。取风速u为8（m／s），规则海浪频率ω取0.3～3（rad／s），步长为0.1（rad／s），采样频率为0.1s。仿真得到随机海浪的波倾角如图1所示。

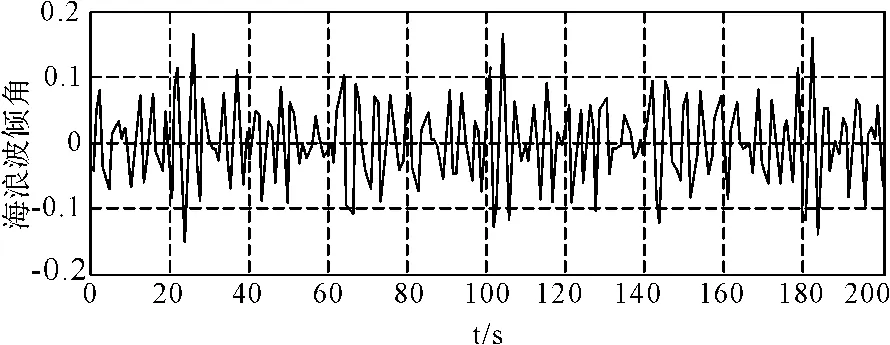
图1 随机海浪波倾角仿真

2.2 随机风浪中的舰船运动仿真

舰船在海上航行有横摇、纵摇、艏摇、纵荡、横荡、垂荡六自由度的运动姿态［8］。本文以横摇为例，将横摇角作为衡量船舶横摇运动的标准。通常，舰船横摇角的影响因素包括船型参数、舰船航速、浪向角及随机风浪等。

假定船体为刚体，忽略它的弹性变形。根据刚体动平衡原理，船舶的平衡条件为力矩为0。按照Conolly理论，则有船舶横摇运动方程［9］为

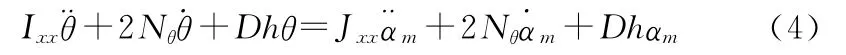
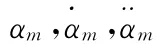
综上，给定船长L＝112.5m，船宽B＝32.2m，吃水d＝5.4m等船型参数，在船速V＝10m／s，浪向角β＝30°，仿真在4～5级海况的随机风浪中船舶的横摇角如图2所示。

图2 船舶横摇角仿真

3 舰船运动姿态预报

自回归模型是常用的时间序列分析模型，运算简单易于执行，适用于线性时间序列分析。而舰船运动姿态一般是非线性、非平稳的，因此，可采用多层自回归模型，使非线性问题线性化，不规则对象规则化。

3.1 自回归预报模型

自回归模型［10］，简称AR模型。该模型仅通过时间序列变量的自身历史观测值来反映有关因素对预测目标的影响和作用。

p阶自回归模型AR（p）的数学形式为

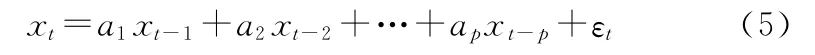
定义：

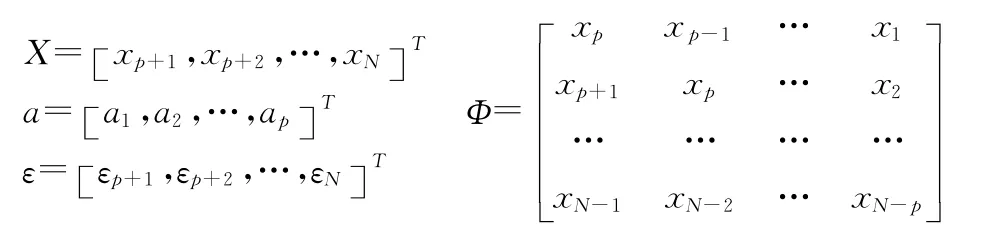
当模型阶数p固定时，用最小二乘法估计模型系数。最小二乘法目标函数为

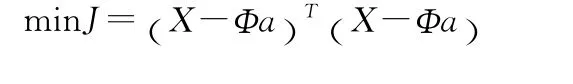
根据矩阵理论可知，参数估计值为

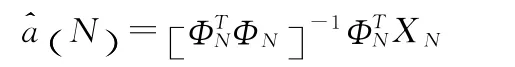
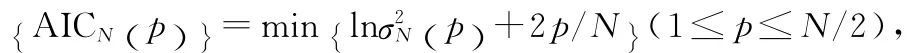
未来第N＋l时刻（l为预报步数）的预报值为

3.2 多层AR预报模型

多层AR预报方法的基本思想是：把动态系统的状态预报问题分为两部分，即对系统的时变参数的预报和在此基础上的对系统状态的预报。这种方法充分注意到了系统的时变特性，因此可以较好地提高预报精度［12］。

多层AR模型是建立在AR模型基础上的，通过分析时间序列的平稳性进行预报。当系统状态不平稳时，采用AR模型对时变参数进行第二层预报，若时变参数的时间序列仍为不平稳，则需对时变参数的参数进行下一层预报，直至最底层参数平稳为止。

多层AR模型形式为

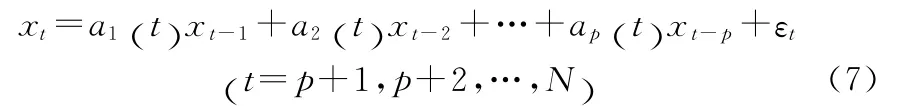
其中，ai（t）为t 时 刻 参 数ai的 值，a1（t），a2（t），…，ap（t）为待估的时变参数序列，p为模型阶数。

根据以上多层AR模型的形式，给出具体实现的步骤如下：

步骤一：利用AR方法建立第一层模型。

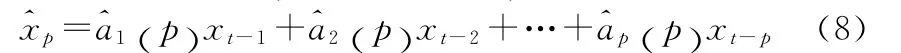
多层AR模型是在AR模型基础之上，增加考虑了模型参数的时变性。令多层AR模型在p＋1时刻的时变参数为AR模型求解所得参数：

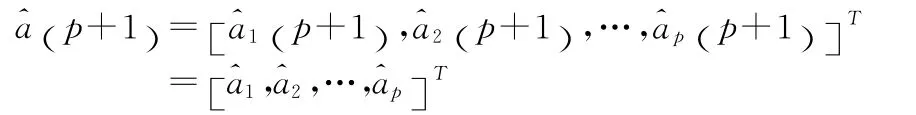
根据p＋1时刻的时变参数及最小二乘法，可以估算出p＋1到N时刻的各参数值。具体如下：

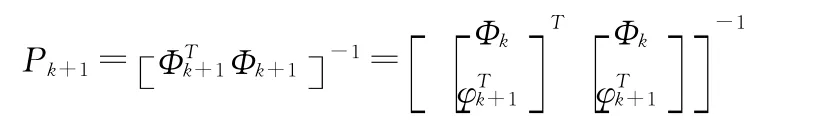
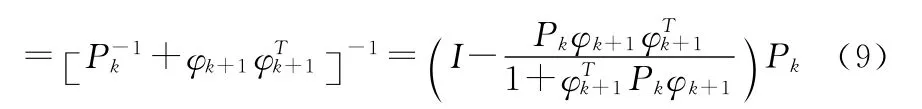
因此可得：

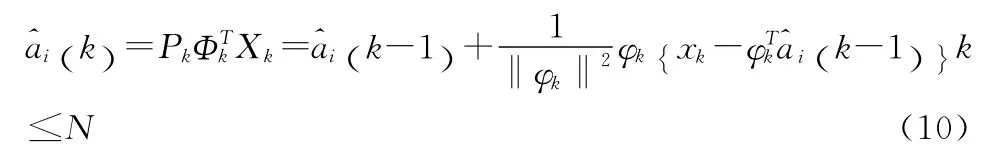
对参数进行平稳性检验的方法有相关系数法、游程法等。若序列为平稳序列，则算法到该层结束，利用AR模型进行各时序的预报即可。若不平稳，则需建立下一层级的多层AR模型。

步骤四：根据步骤三的检验结果，建立多层AR模型，直至参数序列为平稳序列。

步骤五：利用预报得到的时变参数值对原序列值进行预报。

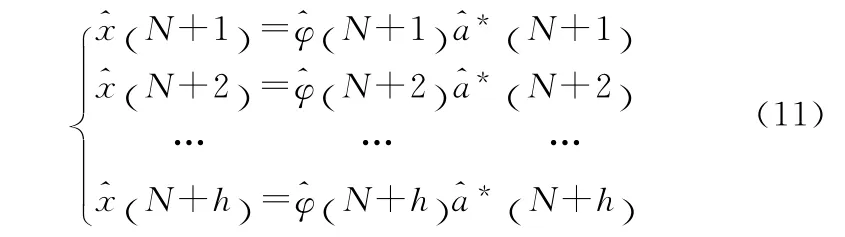
4 仿真预报结果及分析

船舶的运动姿态仿真为预报方法评价提供数据。具体风浪参数及船型参数见2.1节和2.2节中利用的仿真参数。根据自回归预报方法对数据量的需求，本文利用第41s～80s的横摇角数据建立预报模型，并分别利用此后6s和15s的数据进行预报检验。其中一次运行得到的预报结果如图3、图4所示。

图3 6s的横摇角预报图

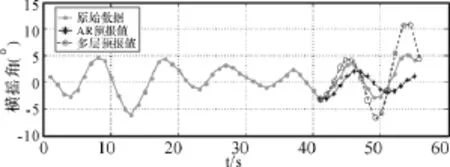
图4 15s的横摇角预报图

运用AR模型及多层AR模型对船舶横摇进行预报，统计方差、绝对误差和相对误差等误差指标，对预报的准确性进行评价，误差结果见表1。在对船舶横摇6s预报时AR方法的平均相对误差为1.01，较难满足预报精度，多层AR方法预报的平均相对误差为0.1708，较AR模型提高了预报的精度；15s预报中多层AR方法优越性不如极短期预报明显。分析可知主要原因在于多层AR模型在对时变参数进行预报时放大了时变参数对原始序列的影响。综上，多层AR模型在一定程度上改进了AR模型，提高了预报精度和预报时长，改善了预报效果。

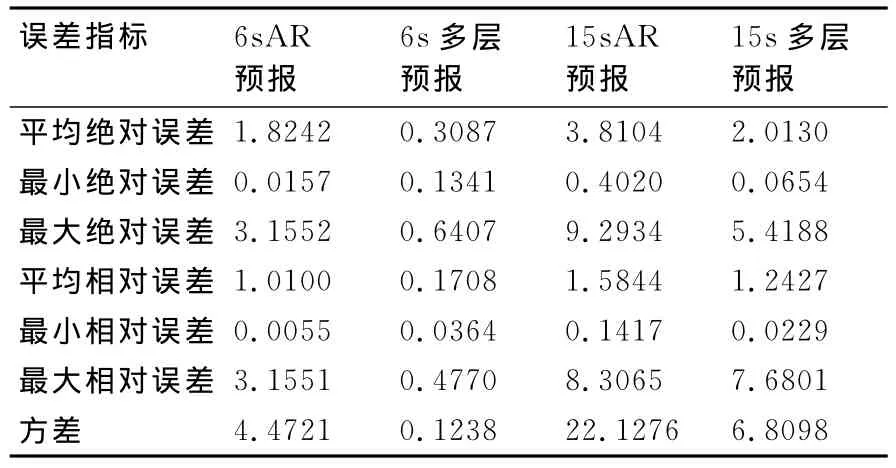
表1 预报误差比较表

5 结语

舰船的运动姿态的仿真与预报研究极为重要。本文从频域角度进行随机风浪的仿真，据此仿真获取横摇角数据，在此基础上，采用AR模型和多层AR模型进行横摇角的预报。多层AR模型可应用于舰船其它自由度的运动姿态预报中，该方法能解决非线性预报问题，较AR方法有一定的改进和提高。

［1］赵希人.具有艏前波观测量的大型舰船姿态运动极短期预报［J］.船舶力学，2003，7（2）：39－44.

［2］翁震平，顾民，刘长德.基于二阶自适应Volterra级数的船舶运动极短期预报研究［J］.船舶力学，2010，14（7）：732－740.

［3］彭秀艳，赵希人，高奇峰.船舶姿态运动实时预报算法研究［J］.系统仿真学报，2007，19（2）：267－271.

［4］王燕.应用时间序列分析［M］.北京：中国人民大学出版社，2005：5－8.

［5］陈远明，叶家玮，张兮龙.船舶运动的极短期预报试验［J］.船海工程，2010，39（1）：13－15.

［6］Gunther F.Clauss.Dramas of the sea：episodic waves and their impact on offshore structures［J］.Applied Ocean Research，2002，24：147－161.

［7］马雪倩，叶锡君，谢忠红.基于模型的海浪模拟仿真［J］.计算机工程与设计，2009，30（2）：446－447.

［8］Tristan Perez.Ship Motion Control［M］.Trondheim：Norwegian University of Science and Technology，2005：18－26.

［9］Nayfeh A H，Sanchez N F.Stability and complicated rolling responses of ships in regular beam seas［J］.International Shipbuilding Progress，1990，37（412）：331－352.

［10］马洁，韩蕴韬，李国斌.基于自回归模型的船舶姿态运动预报［J］.舰船科学技术，2006，3（28）：28－30.

［11］赵建军，肖雄波，杨利斌.基于AR模型和ZMNL变换的分布海杂波仿真方法［J］.计算机与数字工程，2011，39（8）.

［12］韩志刚.多层递阶方法及其应用［M］.北京：科学出版社，1989：139－141.