小波阈值去噪方法在多普勒雷达测速系统中的应用＊

陈 铖 刘昌锦

（陆军军官学院 合肥 230031）

1 引言

传统信号的去噪方法常用短时傅里叶变换，将信号划分为许多小时间段通过傅里叶变换分析每一段时间间隔，以确定该时间间隔内包含的信号频率，滤除噪声频率，再通过傅里叶逆变换恢复信号。

多普勒信号中的噪声主要是随机加性噪声，这种噪声会极大影响对测速数据的统计和处理，对系统稳定和数据可靠性产生危害，因此必须加以滤除。多普勒测速系统通常采用的去除噪声方法即为短时傅里叶变换法，由于噪声的能量一般集中于一定的频段，而信号频谱则分布于一个有限区间，根据这一特点，用傅里叶变换将含噪信号变换到频域，然后采用低通滤波器进行滤波。但是当信号和噪声的频带相互重叠时该滤波方法往往在抑制噪声的同时也将信号的边缘部分变的模糊；而高通滤波器可以使边缘更加突出但背景噪声同时被加强。因此，基于傅里叶变换的去噪方法在保护信号局部性和抑制噪声之间有矛盾。

相比之下，小波变换则具有良好的时频局部化性质，通过小波变换可以更容易地分离出噪声或其他不需要的信息，因此小波变换在信号噪声分析中有着越来越广泛的运用。

2 噪声模型的建立

设长度为N的多普勒信号s（n）被噪声污染后成为u（n），则基本噪声模型为

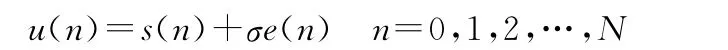
其中e（n）为噪声，σ为噪声强度。多普勒系统中，通常情况下可以认定e（n）为高斯白噪声，且σ＝1。

由于小波变换是线性的，所以对含噪信号进行小波变换等于信号的小波变换与噪声的小波变换之和［1］。基于这一特点，小波去噪的基本方法是：首先对经过预处理的含噪信号进行多尺度小波变换，然后在各尺度下尽可能增强信号的小波系数并去除噪声的小波系数，最后重构信号［2］。

3 小波分析的降噪过程

通过以上分析，小波去噪的过程如下：

1）分解过程：选定一种小波，对信号进行N层小波分解；

2）作用阈值过程：对分解得到的各层系数选定一个阈值，并对细节系数作软阈值处理；

3）重建过程：降噪处理后的系数通过逆小波变换重建恢复原始信号。

该过程基于如下基本假设，即携带信息的原始信号在频域或小波域能量相对集中，而噪声的能量谱相对分散，此时去噪的效果最佳［3～4］。小波去噪过程如图1，其中u为污染信号，e为噪声，s为所需信号。

图1 小波降噪模型

4 小波阈值去噪

该方法在最小均方差意义下可达近似最优，并且可得良好的视觉效果，因此是信号处理中最常用的小波去噪方法［5］。

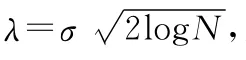
图2 对直线作用硬阈值和软阈值的结果

软阈值：

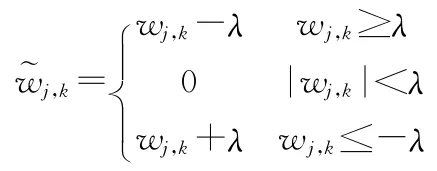
硬阈值：

图2显示了两种阈值情况的不同结果。

去噪结束后再进行逆小波变换，得到恢复的原始信号的估计值。

5 阈值去噪实验及改进

为了说明阈值去噪在多普勒信号分析中的可行性，以下通过Matlab仿真对含有标准白噪声的Doppler信号进行去噪，去噪时选择合适的小波基很重要，小波基的形状要尽可能地贴近原信号波形，这样能取得较好的效果［8～9］，因此试验选择sym6小波基分析。

图3中横轴为时间单位，纵轴表示信号的幅度值。可以看出在图像视觉上软阈值去噪效果不如硬阈值去噪效果，硬阈值可以保留信号的特征，但在平滑方面有所欠缺；而软阈值去噪通常会使去噪后的信号平滑，但会丢失掉一部分原始信号信息。去噪前后在能量及标准差方面对比如表1所示。

表1 去噪效果对比表

在均方误差意义上硬阈值法优于软阈值法，但是由于硬阈值处理函数在λ处不连续，所以得到的信号会产生附加震荡出现伪吉布斯现象（Pseudo－Gibbs），不具有原始信号的平滑性［11］。因此可对硬阈值处理函数作一定改进，采用加权平均方法优化处理函数如下：

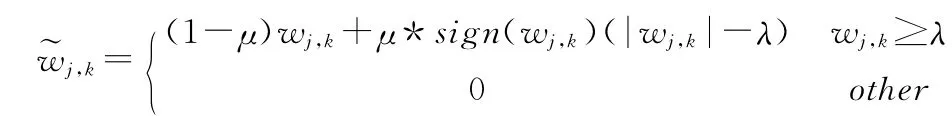
并令

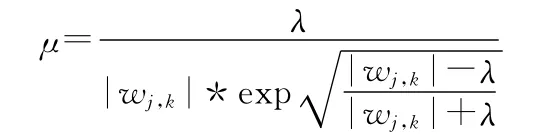
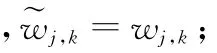
图3 Doppler信号去噪效果

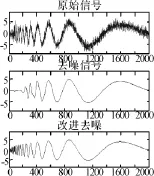
图4 改进阈值后去噪效果

6 结语

仿真结果表明利用小波变换对多普勒信号进行去噪在恢复原信号的光滑性及相似性方面比传统方法即傅里叶变换去噪效果好，原因如下：

1）低熵性，小波系数的系数分布使得信号变换后熵降低；

2）多分辨率性，由于小波函数具有多分辨率特点，因此可以很好地刻画信号的非平稳特征；

3）多样性，由于小波变换可以灵活选择变换基，所以可以根据信号的不同特征选择不同的小波基进行分解变换。

小波变换抑制噪声也有如下缺点：小波变换去噪后对信息能量的保留不如傅里叶变换抑制噪声效果，是一种牺牲能量保持最高相似度的去噪方法；小波变换计算量大，计算方法不如傅里叶变换快速，仍需改进；同时经常采用的小波变换抑制噪声是整体缩减细节系数，在细节的保留上不够精确，有待提高。

［1］关履泰.小波分析方法与应用［M］.北京：高等教育出版社，2007：79－83.

［2］孙延奎.小波分析及其应用［M］.北京：机械工业出版社，2005：220－223.

［3］张德丰.MATLAB小波分析［M］.北京：机械工业出版社，2009：91－92.

［4］秦亚辉，冯景辉，陈立定.基于小波变换的信号去噪方法研究［J］.信息技术，2010（1）：61－63.

［5］李兴梅，龚晓峰，王旭，等.小波包阈值法在无线电信号去噪中的应用研究［J］.现代电子技术，2009（1）：52－53.

［6］MA Liang，HUANG Weizhi，XIAO Zhitao.Study on Denoising Based on the Wavelet Transform［J］.Semiconductor Photonics and Technology，2010，16（1）：29－34.

［7］周健，龙兴武.小波分析在激光多普勒信号处理中的应用［J］.强激光与粒子束，2010，22（12）：2807－2812.

［8］Alexander Tartakovsky，Skirmantas Kligys，Anton Petrov.A－daptive sequential algorithms for detecting targets in a heavy IR clutter［C］／／Signal and data processing of small targets 1999，Processing of SPIE，1999，3809：119－130.

［9］Duff A L，Plantier G，Valière J C，et al.Analog Sensor Design Proposal for Laser Doppler Velocimetry［J］.IEEE Sensors Journal，2004，4（2）：257－261.

［10］牛小东.一种改进小波收缩阈值的信号消噪算法［J］.计算机与数字工程，2011，39（3）.

［11］杨建国.小波分析及其工程应用［M］.北京：机械工业出版社，2005：108－109.