约束变换型地图概括模式

钟业勋 ， 童新华

（1.广西师范学院 资源与环境科学学院，广西 南宁 530001；2.广西测绘地理信息局，广西 南宁 530023）

地图概括是地图的基本特性之一.地图比例尺愈小，地图概括程度愈大.地图概括的实质就是在地图上表示制图对象基本的、典型的面貌和主要特征及其相互关系，是制图对象质量和数量特征的概括，是以集体的概念取代个体的概念，将局部的和细小的抽象化，以便更明显地反映制图对象空间分布的主要特征[1].地图表示的详略与地图比例尺的相关性表明，地图概括是从大比例尺指向小比例尺方向的，是单向的不可逆过程.在相关的两幅地图A与B之间存在着一种映射或变换关系，即h∶A→B.地图概括实质上是点集之间在某种约束条件下的变换.根据这一原理，笔者对约束变换型地图概括概念分别给出了数学定义.

1 地图概括模式及变换的定义

1.1 地图概括模式

地图概括也称制图综合.不同的学者对制图综合提出过不同的分解模式，包括最常见的三算子模式（选取、概括和移位）、四算子模式（选取、概括、合并和移位）、两类七算子模式（纯几何综合：简化、夸大、移位；几何/概念综合：合并、选取、类型化、强调）及GIS界的二十算子模式[2].考虑到综合算子间的相互关系和逻辑顺序，并根据地图概括中普遍存在和应用的实践，笔者提出了十一算子模式，即选取、舍弃、派生、简化、增补、夸大、合并、分割、移位、类型化和强调[3-4].

1.2 变换的定义

定义1 变换 设X是集合，X上的一一对应为X上的变换，有限集上的变换又称为置换[5].

设地图A、B为X的子集，X⊃A,B,∃h∶A→B，若点集a∈A→h(a)∈B,h(a)∈B,h(a)∈B便是a在h下的变换.A和B都是地图符号的有限集，故其变换即是置换.地图概括中的选取、舍弃等概念，也就是在一定的约束条件下，用a∈A的点集到h(a)∈B的变换来描述，即用B中的点集h(a)∈B置换A中的对应点集a∈A的方式来定义.

2 地图概括模式的数学定义

定义2 选取 ∃h∶A→B和选取阈值k∈A，若点集a1∈A的变换满足：

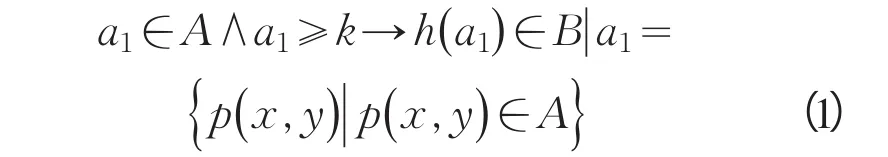
则称a1为选取元素，h(a1)∈B为B对h(a1)的选取.

例如，若规定单线河的选取标准是k=1.5 cm，大于和等于1.5 cm的单线河就是a1.对不同性质的事物的选取阈值，有不同的a1.h(a1)∈B表明，这些元素都被B选取

定义3 舍弃 ∃h∶A→B和选取阈值k∈A，若点集a2∈A的变换满足：

则称a2为舍弃元素，h(a2)∉B即B对h(a2)的舍弃.

定义4 派生 ∃h∶A→B和选取阈值k∈A，若点集a3满足：

则称a3=g（a2）为由舍弃点集a2导致的派生元素，简称派生.h(a3)∈B为B对派生元素的选取.

岸线、等高线的舍弯取直的概括中，舍去的小弯曲即为a2，连结舍弃元素两端的短线即为派生元素.

定义5 简化 ∃h∶A→B，存在选取元素a1，舍弃元素a2和派生元素a3，若变换满足：

则称h(a4)∈B为简化，它是选取、舍弃和派生的复合运算.

定义6 增补 ∃h∶A→B，若点集a5满足：

则称a5为增补元素.

一般情况下，a5的性质是A的原有位置上所没有的，h(a5)∈B表明，它是B中增补的元素.

定义7 夸大 ∃h∶A→B，地图符号s∈A，若点集a6∈A∧a6≠φ存在并满足：

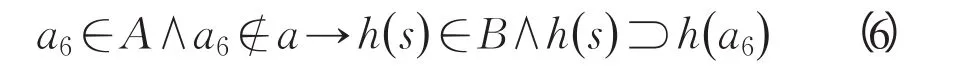
则称h(s)为s的夸大.

夸大是使A中不属于s的非空点集a6变换后被h(s)包含的变换.被纳入h(s)中的点集a6愈大，符号夸大愈大，a6的大小是夸大的度量.

则称h(s)为s的合并.合并是从A中一个分离并的点集到B中的连通集h(s)的变换.

定义9 分割 ∃h∶A→B，若地图符号s=(b1⋃b2)∈A，若变换满足：

则称h(s)为s的分割.分割是将A中的连通集到B中的分离并的变换[6].分割是合并的逆变换.

定义10 平移 将平面上的点p按定向量k的方向移动到p’点，使pp’=k的变换，叫做平移变换，简称平移[7].

定义11 移位 ∃h∶A→B，若变换满足：

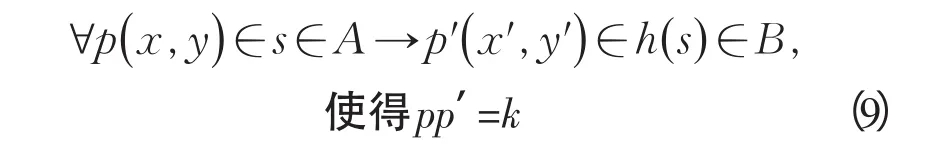
则称为s的移位.pp’=k是移位的度量.

定义12 类型化 ∃h∶A→B，分类 Xa∈A，Xb∈B，若变换满足：

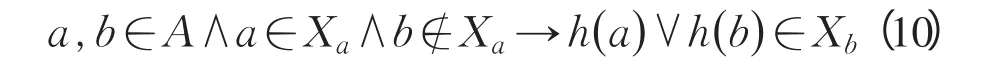
则称h(a)∨h(b)∈Xb为类型化.类型化是在A中分类的基础上进行归并概括.

例如，土地利用按二级分类（Xa）时，铁路、公路、农村道路、民用机场、港口码头各成一类；而按一级分类（Xb）则被归并为交通用地类.

定义13 强调 设a1和a2分别为A的选取元素和舍弃元素，F为强调因素集（如地理特征）.若变换满足：

则称对a2的强调.

强调是把舍弃元素中具有强调因素（如地理特征）的部分特别作为选取元素的处理.强调是满足a2∈F∧a2∈A条件下的选取，还伴随着一定程度的夸大与移位，是选取、夸大和移位的复合运算.

3 结语

地图概括方向从大比例尺地图指向小比例尺地图，因此，概括行为必定存在着从资料底图A到新编图B的映射或变换h∶A→B.地图概括中的选取、舍弃、派生、简化、增补、夸大等形式，实质上是在某种约束条件下的点集间的变换.不同的约束条件，对应着不同的概括模式.本文对地图概括中常见的11种概括模式分别给出了数学定义，从而使这些地图概括概念获得了精密的数学形式和定量描述，揭示了概念的本质特征和内在联系.

[1]廖克.现代地图学[M].北京：科学出版社,2003.

[2]母河海.地图信息自动综合基本问题研究[J].武汉测绘科技大学学报,2000,25（5）：377-384.

[3]Zhong Y X,Wei W Z,Hu Y J,et al.Mathematical Definition of Operators for Cartographic Generalization[J].Geo-spatial Information Science,2003,6(1)：70-73.

[4]李占元,钟业勋.地图编绘的布尔代数原理及制图综合算子数学模型[J].武汉大学学报：信息科学版,2005,30（5）：431-434.

[5]章炯民,陶增乐,柳银萍,等.离散数学[M].上海：华东师范大学出版社,2009.

[6]李孝传,陈玉清.一般拓扑学导引[M].北京：高等教育出版社,1982.

[7]罗淼,严虹,廖义琴.几何学概论[M].北京：清华大学出版社,2011.