输电塔架设计中的离散优化方法研究

李 林，宋梦娇，王达达，陈晓云

(1.华北电力大学 能源动力与机械工程学院，北京 102208)

(2.云南电力试验研究院，云南 昆明 650217)

0 引言

随着我国在高压输电线路建设的步伐加快，兼顾经济性和安全性的输电塔架设计越来越引起重视。同样尺寸的塔架所能承受的荷载取决于组成塔架的每根型材的截面尺寸和布置型式。因此，如何合理的布置结构构件的截面尺寸，使每根杆件都能最大限度地承受荷载尤为重要。近年来，文献[2，3]为了解决型钢离散变量的特点，根据桁架的受力特点及满应力法的设计原理，在优化设计的迭代过程中利用拟合函数把型钢截面尺寸当作连续变量来处理，而在设计结束后再根据各杆件的截面尺寸，由型钢表中选择合适的截面型号，但此方法通过连续变量协调所取的型号不能保证使目标函数达到最优结果。文献[4]以力学准则法为基础，提出了一种求解离散变量结构优化设计的拟满应力方法，直接求解具有应力约束和几何约束的离散变量结构优化设计问题，但此算法过程中使用到二进制遗传编码，应用于塔架结构优化中时，由于输电塔架杆件数和荷载工况较多，在编制寻优程序出现错误不易查找。本文为了解决和改进现有设计方法存在的问题，结合输电塔架设计原则，提出一种基于离散变量并考虑了压杆稳定性的满应力优化设计方法，使塔架在满足多种工况荷载条件下，具有合理的结构承载能力，以达到塔架重量最轻，降低工程成本的目的。同时，此算法也为改进现有塔架典型设计和加固已有输电塔架提供可行的算法基础。

1 现行满应力优化设计方法

满应力设计的设计思想就是对一个既定的结构布局，通过调整构件的截面尺寸，使结构的每一构件至少在一种荷载情况下的应力达到容许应力，此时就认为结构重量最轻。对于静定结构，由于杆件的内力不随截面积而变，按满应力准则设计，一次就可以使结构达到最轻。而对于超静定结构，由于杆件的内力随截面积而变，不能一次求得最优解，可以采用迭代计算的方法使其最终收敛到最优解。

1.1 满应力方法步骤

(1) 设 定 初 始 截 面 积 A0=[a1，a2，…ai…，am]，ai为第i根杆件的截面积;

(2)进行结构有限元分析，计算各杆件在多重工况荷载作用下的轴力 N=[N1K，N2K，…，NmK]T，工作应力 σ =[σ1K，σ2K，…，σmK]T，其中，K为荷载工况号;

(3)计算各种荷载工况下的应力比矩阵D=[D1K，D2K，…，DmK]T，其中，DiK= σiK/[σ]i，[σ]i为第 i根杆件的许用应力;

(4)计算最大应力比矩阵 D=[D1，D2，…，Dm]T，Di为第i根杆件在各荷载工况中的最大应力比;

(5)判断收敛条件，设计一个精度控制值e，当每个杆件都满足|1–Di|≤ε，则迭代结束，否则计算新的截面积ai(j+1)=Diai(j)，返回到第二步继续循环计算。

1.2 现行满应力优化法在输电塔架超静定结构中运用所存在的问题

(1)由于塔架结构中角钢的尺寸现已规范化，因此塔架优化模型中的设计变量角钢截面积为离散变量，而传统满应力优化设计中设计变量为连续变量，故塔架优化模型用传统满应力优化无法解决。很多学者[2，3]为了用满应力法优化离散变量的塔架模型，找出了角钢截面积与惯性半径的数学拟合关系、压杆稳定系数与杆件长细比的数学拟合关系，把离散变量的数学模型转化为连续变量的数学模型，从而解决了这一问题，但由此带来了另一个问题，就是要对优化结果进行取整计算，即按照国标中规定的角钢截面大小来调整优化结果，这样一来又进一步的增大了工作量，又不能保证最终优化结果是最优结果。

(2)超静定结构的满应力优化设计中，目标函数与最优化条件没有任何直接联系，也就是说满应力设计并不能保证使结构重量最轻，除非将约束条件方程和使目标函数最小联立起来求解，才能保证结构重量最轻。所以，除静定结构外，满应力优化设计不一定具有最小重量。

(3)传统满应力设计计算中，只考虑了杆件应力大小，而忽略了压杆的稳定约束。在塔架结构计算模型中，必须进行压杆的稳定验算，故需对此进行改进。

2 改进的离散变量满应力优化方法

2.1 输电塔模型一般假设

(1)假定输电塔杆件为桁架结构，杆件两端的节点都是理想的没有摩擦的铰接;

(2)忽略螺栓、插板、法兰、金具的影响，建模时不考虑其质量和刚度的影响;

(3)对边界条件的处理:假设基础对输电塔腿的约束为固定约束;

(4)外力都作用在节点上。

2.2 数学模型[10]

2.2.1 设计变量

主设计变量为型钢 (角钢、双角钢)型号，辅助设计变量为型钢号所决定的横截面面积、角钢宽度、角钢厚度、平行轴半径、最小轴半径等。设计变量按型钢截面积的升序排列，即

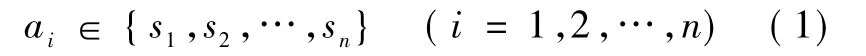
式中:{s1，s2，… ，sn}为离散变量集，型钢标准截面积，mm2;ai为第 i根杆件截面积，Ai=[a1，a2，… ，am]T，mm2;n 为标准角钢型号总数;m为杆件总数。

2.2.2 目标函数

输电塔结构的优化目标函数是以经济性为主的结构总重量的函数，包括受力杆件的重量以及辅助材和节点螺栓、插板的重量。则目标函数为

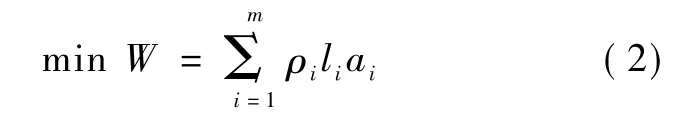
式中:ri为第i个杆件的材料密度，kg/mm3;li为第i个杆件的长度，mm。

2.2.3 约束条件

(1)轴心受力构件的强度计算:

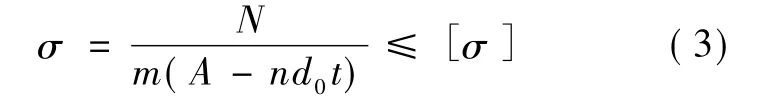
式中:N为轴心拉力或轴心压力设计值，N;A为构件毛截面面积，mm2;n为同一截面上的螺栓孔数;d0为螺栓孔直径，cm;t为构件厚度，cm;[σ]为钢材的强度设计值，N/mm2;m为构件强度折减系数。

(2)轴心受压构件的稳定计算:

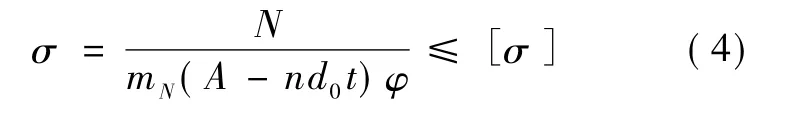
式中:A为构件毛截面面积，mm2;mN为压杆稳定强度折减系数，根据翼缘板自由外伸宽度b与厚度t之比计算确定;j为轴心受压构件稳定系数。

2.3 优化算法

(1) 设 定 初 始 截 面 积 A0=[a1，a2，…ai…，am]，ai为第i根杆件的截面积;

(2)进行结构有限元分析，计算各杆件在多重工况荷载作用下的轴力 N=[N1K，N2K，…，NmK]T，工作应力 σ =[σ1K，σ2K，…，σmK]T，其中，K为荷载工况号;

(3)确定每一根杆件的许用应力[σ]，构件工作条件系数，m;

(4)按满应力计算每个工况下的最小截面积，查标准角钢表选取标准型号;

(5)压杆稳定计算，调整截面积 (计算稳定强度折减系数、轴心受压构件稳定系数、长细比修正系数);

(6)比较每根杆件在不同工况下的截面积，选出最大截面积;

(7)计算每个杆件的面积比Di=ai(n–1)/ain，其中，n为迭代次数;

(8)判断收敛条件，设计一个精度控制值ε，当每个杆件都满足|1–Di|≤ε，则迭代结束，否则返回到第二步继续循环计算。

3 算例

3.1 模型

下面以常见干字型输电塔架2F2－SZ1型220 kV双回路直线塔为例，运用传统满应力优化方法和上述改进的满应力优化方法进行选材优化设计，通过数据分析对比，论证本文方法的可靠性与优越性。

本文所选输电塔架为空间超静定桁架结构，由226个节点657个杆件单元组成，呼高33 m，全高49.3 m，根开7.99 m，原设计参与计算的构件重量为9 151.4 kg。

在本文所述优化设计中，杆件型材为单根等边角钢和双角钢，可供选择的截面型号有92种，最小截面型号为L40 cm×3 cm，最大截面型号为L250 cm×35 cm。杆件材料为 Q235钢和 Q345钢，材料密度为 7.85×10－6kg/mm3，弹性模量为2.06×105N/mm2，共计算45组不同的荷载工况，其中挂线荷载和风荷载的加载点共150个。钢材的强度设计许用值见表1。

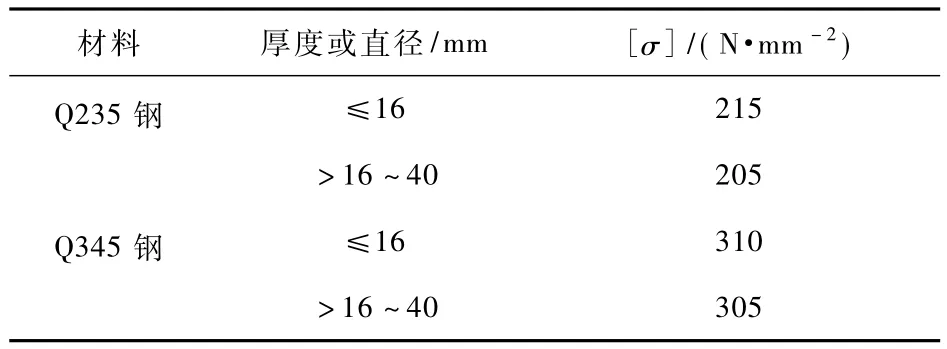
表1 钢材的强度设计许用值Table 1 The design value of steel strength

3.2 计算结果及分析

由于塔架计算杆件较多，在此仅提取受力较大的输电塔架塔腿部位前两个节间的8根主材受力变化和截面积的变化情况来进行说明分析。

杆件截面尺寸优化的初始值可取典型设计中的杆件截面尺寸。图1所示，截取了前两个节间共8根主材的截面尺寸变化数值，由图中曲线数据可知，各杆件的截面尺寸经过数次迭代达到收敛。

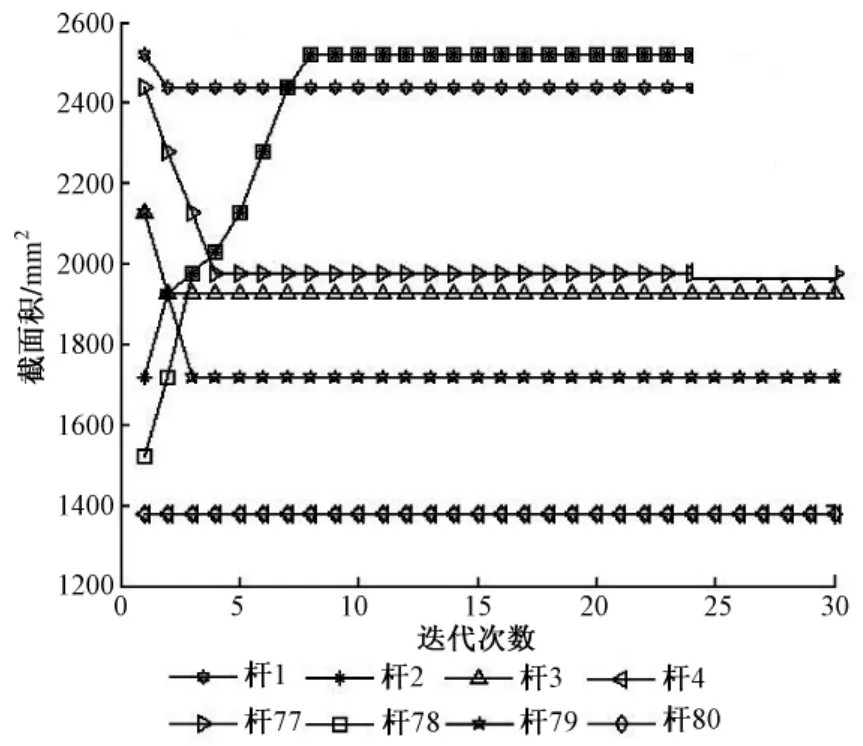
图1 部分主材截面尺寸优化过程Fig.1 The optimization process of part leg angle size

图2所示，同样截取前两个节间的8根主材在每个工况下的最大应力比的变化情况，都在0.67～0.86的范围内变动，能够保证结构的强度和稳定，从而证明本文方法的可靠性。

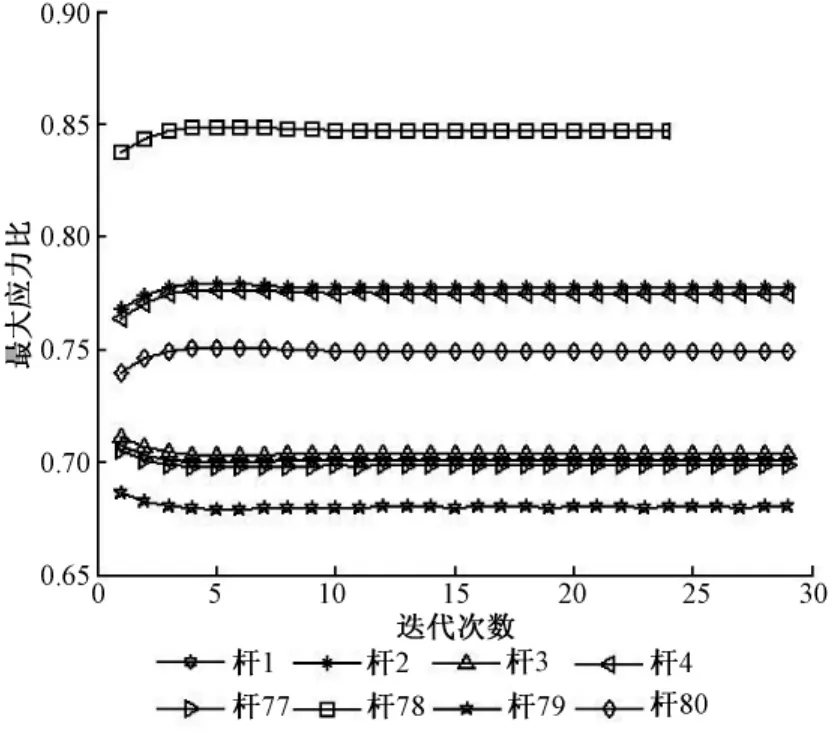
图2 部分主材最大应力比变化过程Fig.2 The changing process of part leg angle maximum stress

图3，4为两种方法下目标函数塔架总重量的迭代变化曲线图。图3所示的传统优化方法中，目标函数在迭代42次时开始在6 200 kg上下震荡，表明传统优化方法不能很好地适用于输电塔架类的静不定结构。图4所示的改进优化方法中，目标函数在迭代12次时趋于稳定并达到最佳结果，得到的参加计算的构件总重量为5 190 kg，相比原有设计大大减小，从而降低了工程成本。

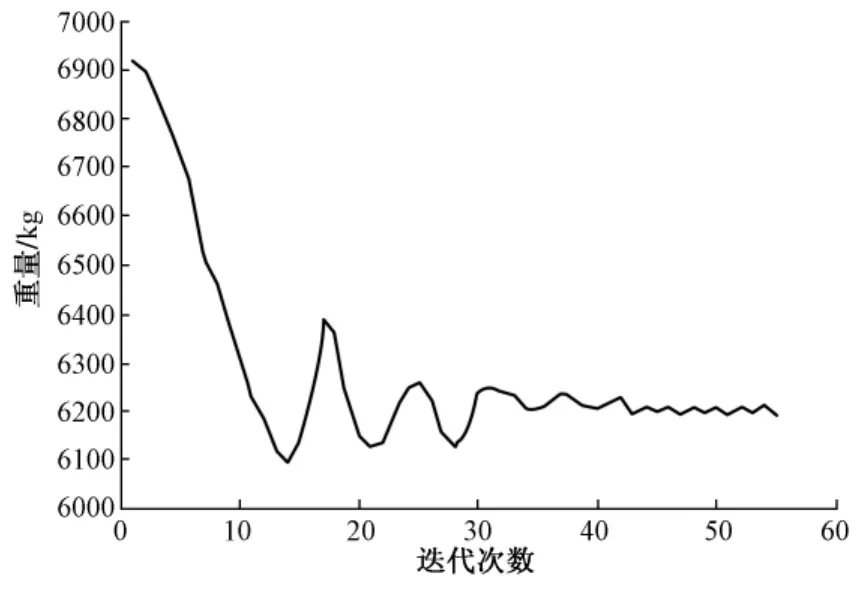
图3 传统优化方法的塔架总重量变化图Fig.3 The changing map of tower total weight of traditional optimization

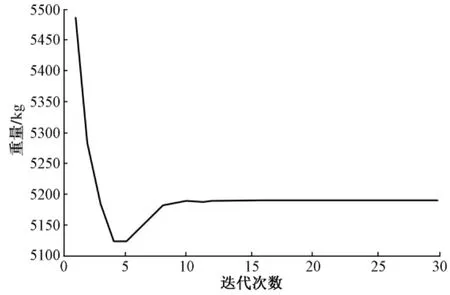
图4 改进优化方法的塔架总重量变化图Fig.4 The changing map of tower total weight of improved optimization

4 结论

为了使满应力优化设计更好的应用于输电塔选材计算中去，本文在传统满应力优化设计思路的基础上进行改进，提出了一种适用于离散变量并考虑了压杆稳定性的满应力优化设计方法。借助C语言编制优化程序，根据实际荷载组合及约束条件，对已有的常见干字型输电塔架进行杆件截面优化选材。算例分析表明，该算法不仅保证塔架结构符合全部设计工况，而且达到了结构总重量最小化的目的，运用本文改进满应力优化方法能够大大提高优化迭代速率，优化结果令人满意。此算法不仅解决了连续变量圆整后不能保证最优结果的问题，而且由于编制出的源程序不使用二进制编码，方便查找错误和进行二次开发，为改进现有塔架典型设计和加固已有输电塔架提供可行的算法基础。

[1]刘夏石．工程结构优化设计[M]．北京:科学出版社，1984．

[2]任治章，温伟力，赵冰．钢桁架优化设计中稳定及收敛问题的有效解法[J]．力学与实践，2007，29(5):24－28．

[3]陈孝珍，张学军，任治章．型钢桁架满应力优化设计研究[J]．机械设计与制造，2008，12:24 －26．

[4]郭鹏飞，韩英仕．离散变量结构优化设计的拟满应力遗传算法[J]．工程力学，2003，20(2):95 －99．

[5]隋允康，乔志宏，杜家政．采用相似变换解决含压杆稳定约束的桁架满应力设计[J]．工程力学，2005，22(6):112－116．

[6]郭惠勇，李正良，罗乐．基于离散变量的大跨越输电塔架构不同优化方法研究[J]．工程力学，2009，26(12):181－188．

[7]李文雄．桁架结构优化设计的满应力法仿真研究[J]．计算机仿真，2012，29(1):395 －398．

[8]郭惠勇，曾虹，李正良．离散变量结构优化设计的理论与方法[J]．重庆科技学院学报，2010，12(4):97 －99．

[9]樊涛，刘政，韩刚，王坚．基于满应力的桁架梁轻量化设计[J]．起重运输机械，2012，1:36 －38．

[10]张殿生．电力工程高压送电线路设计手册[M]．北京:中国电力出版社，2003．

[11]崔磊．输电塔结构优化设计理论及应用[D]．上海:同济大学，2009．

[12]Sheu C Y，Schmit L A．Minimum weight design of elastic redundant trusses under multiple static loading conditions[J]．AIAA Journal，1972，10(2):155 － 162．

[13]Templeman A B，Yates D F．A segmental method for the discrete optimum design of structures[J]．Engineering Optimization，1983，6:145 － 155．

[14]Tong W H，Liu G R．An optimization procedure for truss structures with discrete[J]．Computer and Strutures，2001，79:156 －162．

[15]Luh G C，Lin C Y．Optimal design of truss structures using ant algorithm[J]．Journal of Strutural Engineering，2004，36(5):741－751．