原－对偶内点法和预测－校正内点法在最优潮流的应用

杨利水，杨 旭，顾家翠

(1．保定电力职业技术学院，河北 保定 071051;2．深圳供电局，广东 深圳 518000;3．广东电网公司教育培训评价中心，广东 广州 510520)

0 引言

电力系统最优潮流OPF(Optimal Power Flow)是一个复杂的非线性规划问题，要求在满足特定的电力系统运行和安全约束条件下，通过各种控制手段实现预定目标最优的系统稳定运行状态。由于最优潮流是同时考虑网络的安全性和经济性的分析方法，因此在电力系统的安全运行、经济调度、电网规划、复杂电力系统的可靠性分析、传输阻塞的经济控制等方面得到广泛的应用[1]。

现今求解最优潮流的方法非常繁多，归纳起来有二次规划法、非线性规划法、线性规划法、内点法以及混合规划法和人工智能方法等[2]。文献[3]通过雅可比矩阵进行变换建立无功优化的线性规划模型，并提出原对偶仿射尺度内点法求解线性规划模型。文献[4]针对无功优化模型中含有离散变量的问题，采用非线性原–对偶内点法进行求解。文献[5]结合电力系统的特性，提出了一种基于稀疏技术的原－对偶内点法求解最优潮流问题及一种新的迭代步长和中心方向的修改策略。文献[6]基于改进遗传算法和原对偶内点法提出一种求解无功优化问题的混合算法，有效提高了混合优化算法的整体寻优效率。本文分别对原 －对偶内点法 (Primal-Dual Interior Point Method，PDIPM)和预测－校正内点法(Predictor-Corrector Primal-Dual Interior Point Method，PCPDIPM)的原理进行讨论，并得出后者优于前者，利用Matlab进行仿真验证。

1 最优潮流模型

电力系统最优潮流的数学模型如式 (1)。

目标函数:

式中:PGi为第 i台发电机的有功出力;a0i，a1i，a2i为其耗量特性曲线参数，表示发电成本最小。

以上模型中式 (2)为等式约束 (节点功率平衡方程);式 (3) ～ (6)为不等式约束，依次为电源有功出力上下界约束，无功源无功出力上下界约束，节点电压上下界约束，线路潮流约束。式中:SB为系统所有节点的集合;SG为所有发电机集合;SR为所有无功源集合;Sl为所有支路集合;PGi，QGi为发电机 i的有功、无功出力;PDi，QDi为节点 i的有功、无功负荷;Viθi为节点 i电压幅值与相角，θij= θi－ θj;Gij，Bij为节点导纳矩阵第i行第j列元素的实部与虚部;Pl为线路l的有功潮流，设线路 l两端点节点为 i，j。该模型采用的是节点电压极坐标的表示形式，当然也可以采用节点电压直角坐标的表达形式。

2 最优潮流问题的内点法

内点法最初的基本思路是希望寻优迭代过程始终在可行域内进行，因此初始点应取在可行域内，并在可行域的边界设置“障碍”使迭代点接近边界时其目标函数值迅速增大，从而保证迭代点均为可行域的内点。但是对于大规模实际问题而言，寻找可行初始点往往十分困难。为此许多学者长期致力于对内点算法初始“内点”条件的改造。目前应用较为广泛的有原对偶内点法和预测校正内点法。

2.1 原对偶内点法

为了便于讨论，把最优潮流模型式 (1) ～(6)简化为以下非线性优化模型:

式中:式 (7)为目标函数，是一个非线性函数;式 (8)h(x)=[h1(x)，…，hm(x)]T为非线性等式约束条件，对应于最优潮流模型中式 (2);式(9) 中 g(x) =[g1(x)，…，gr(x)]T为非线性不等约束，其上限为 g(x) =[g1(x)，…，gr(x)]T，下限为在以上模型中共有 n个变量，m个等式约束，r个不等式约束。跟踪中心轨迹内点法的基本思路如下。

将不等约束式 (9)转化为等约束式，并将目标函数改造为障碍函数，得到优化问题B:

式中，l=[l1，…，lr]T和u=[u1，…，ur]T为松弛变量，扰动因子 (或称障碍常数)μ＞0。当li或ui(i=1，…，r)靠近边界时，以上函数趋于无穷大，因此满足以上障碍目标函数的极小解不可能在边界上找到，该问题可用拉格朗日乘子法来解。

优化问题B的拉格朗日函数为

式中:y=[y1，…，ym];z=[z1，…，zr];w=[w1，…，wr]均为拉格朗日乘子。该问题极小值存在的必要条件是拉格朗日函数对所有变量及乘子的偏导数为0，由于此方程组都为非线性，则可用牛顿－拉夫逊法进行求解，并根据极值存在的必要条件可以得到:

由文献[7]发现，当目标函数中参数μ按式(12)取值时，算法的收敛性较差，建议采用:

式中:对偶间隙Gap=lTz－uTw，σ∈(0，1)称为中心参数，一般取0.1，在大多数场合可获得较好的收敛效果，这样可以得到修正方程:

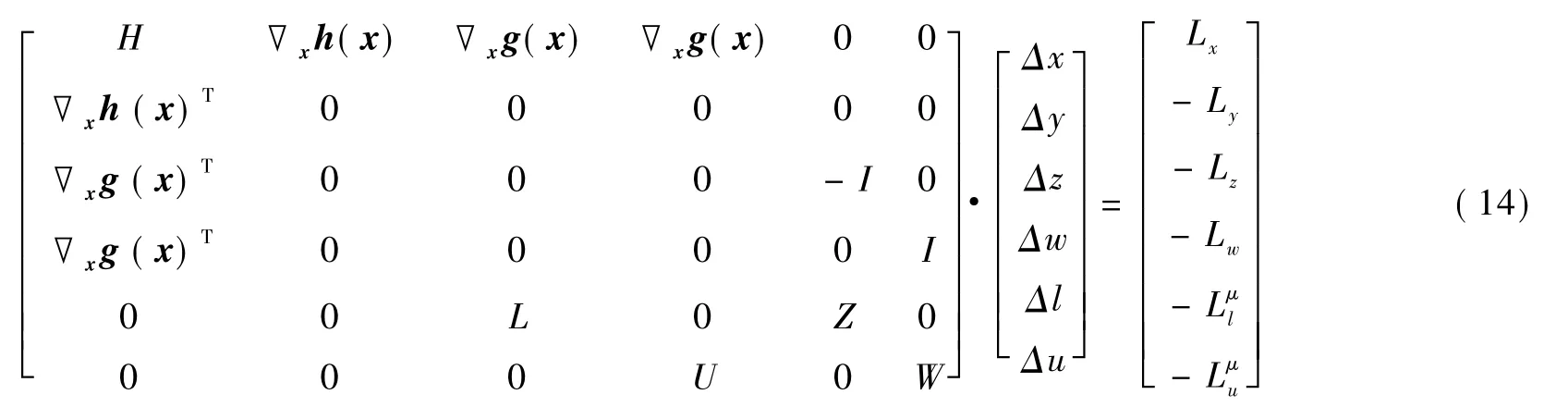
式中，H=－[▽2xf(x)－▽2xh(x)y－▽2xg(x)(z+w)]。

由于修正方程的系数矩阵是一个(4r+m+n)×(4r+m+n)的方阵，因此求解该方程的计算量十分庞大，可以对其进行变换，以减少计算量。

式中:

现在，我们只需要对一个相对较小的(m+n)·(m+n)对称矩阵 (即右下块矩阵)进行LDLT分解，剩余的计算量只是回代。这样，不仅减少计算量，同时简化了算法。

对其进行求解得到第k次迭代的修正量，于是最优解的一个新的近似为

其中步长 αp和 αd为

2.2 预测校正内点法

预测－校正内点法与原－对偶内点法非常相似，只是线性化过程中保留了Ll和Lu的高阶项，正是由于高阶项使得预测校正内点法比原对偶内点法更优越。

写成矩阵形式:

记 λ =(z，l，w，u，x，y)T，而 M，Δλ 分 别 为(19) 式中左边的第 1，第 2项，daf，dce，dco分别为 (19)式等式右边的第1，第2，第3项，则上式可写为

预报校正算法完整的求解修正方程式 (19)，在预报阶段先由方程:

解出仿射方向Δλaf，按式 (17)计算仿射迭代步长αd，αp，然后计算仿射补偿间隙:

并计算仿射扰动因子:

从而可以计算 dce，dco。

在校正阶段，由方程:

解出校正方向Δλco。

最后得到总的原、对偶变量的修正量:

然后按式 (16)对原变量和对偶变量进行更新。值得指出的是，在预报阶段得到Δλaf，μaf后，可直接代入式 (19)，从而得到Δλ。

3 数值分析

本文分别使用 IEEE14，IEEE118，IEEE300系统进行了验证，证明了内点法具有收敛迅速，鲁棒性强的特点。表1给出了不同节点数目的系统在分别用原－对偶内点法 (PDIPM)和预测－校正内点法 (PCPDIPM)进行潮流优化时的迭代次数、迭代时间以及优化前和优化后的目标函数值。可以看出，预测－校正法较之原－对偶法有更好的收敛性和收敛速度，并随着系统节点的变大，这种优越性更明显。图1～6给出 IEEE14，IEEE118，IEEE300系统的仿真曲线。

表1 不同系统迭代次数、运行时间及目标函数值Tab．1 Iterations，operational time and the value of target function of different system

观察1～6仿真图可发现，通过 IEEE 14，IEEE 118，IEEE 300测试系统的仿真计算证明了该两种算法计算结果均趋于收敛，且收敛速度快，鲁棒性好，且未出现数值稳定问题，因此内点法可以在潮流优化计算中得到很好的应用。

通过图1与2、图3与4和图5和6的对比，可以发现在预测－校正算法中燃料费用曲线趋于收敛的速度较原－对偶算法更快，因此预测－校正法较之原－对偶法有更好的收敛性和收敛速度，这是由于预测－校正内点法由于在进行泰勒展开时保留了高阶项。

图1 预测－校正法迭代情况(IEEE14)Fig.1 The iterations of PCPDIPM(IEEE14)

图2 原－对偶法迭代情况(IEEE14)Fig.2 The iterations of PDIPM(IEEE14)

图3 预测－校正法迭代情况(IEEE118)Fig.3 The iterations of PCPDIPM(IEEE118)

图4 原－对偶法迭代情况(IEEE118)Fig.4 The iterations of PDIPM(IEEE118)

图5 预测－校正法迭代情况(IEEE300)Fig.5 The iterations of PCPDIPM(IEEE300)

图6 原－对偶法迭代情况(IEEE300)Fig.6 The iterations of PDIPM(IEEE300)

4 结论

本文分别采用原－对偶内点法和预测－校正内点法进行潮流优化计算，从仿真例子可以看出内点法具有收敛速度快，鲁棒性强，对初值的选择不敏感的特点，并且预测－校正内点法由于在进行泰勒展开时保留了高阶项，所以具有比原－对偶内点法更好的收敛性。

[1]万黎，袁荣湘．最优潮流算法综述[J]．继电器，2005，33(11):80－87．

[2]池哲浩，张洪梁，赵连杰．电力系统最优潮流计算方法[J]．黑龙江电力，2011，33(5):343 －349．

[3]刘明波，陈学军．基于原对偶仿射尺度内点法的电力系统无功优化算法[J]．电网技术，1998，22(3):24 －28．

[4]常鲜戎，张亮平，郑焕坤．非线性原–对偶内点法无功优化中的修正方程降维方法[J]．电网技术，2011，35(5):46－51．

[5]李彩华，郭志忠，樊爱军．原－对偶内点法最优潮流在电力系统中的应用[J]．电力系统自动化设备，2002，22(8):4 －7．

[6]刘方，颜伟，David C．Yu．基于遗传算法和内点法的无功优化混合策略[J]．中国电机工程学报，2005，25(15):67－72．

[7]Polyak R A．Nonlinear rescaling vs．smoothing technique in convex optimization[J]．Math Program，2002，Ser．A(92):197 －235．

[8]Polyak R．Primal-Dual Exterior Point Method for Convex Optimization[J]．Optimization Methods 8 Sottware，2008，23(1):141 －160．

[9]Griva I．Numerical experiments with an interior-exterior point method for nonlinear programming[J]．2004．

[10]Igor G，Polyak R A．1.5－Q-superlinear convergence of an exterior-point method for constrained optimization[J]．2006．

[11]Hande Y Benson，David F S．Interior-point methods for nonconvex nonlinear programming:Filter methods and merit functions[J]．Technical Report ORFE －00 －06，Dept of Operations Research and Financial Engineering，Princeton University， Princeton NJ，2000，2000 －2001．

[12]Igor G．Primal-dual nonlinear rescaling method with dynamic scaling parameter update[J]．Mathematical Programming，2006，Ser．A:237 － 259．

[13]Yasushi K，Nobuyama E．An exterior point approach to the mixed Hm/D-stability synthesis problem[C]．In 5th Asian Control Conference，2004:410 － 416．

[14]Yasushi K，Nobuyama E．A mixed H∞ /D-stability controller design using an exterior-point approach[C]．In 43rd IEEE Conference on Decision and Control(Atlantis，Paradise Island，Bahamas)，2004:263 － 275．

[15]Ibsais A，Ajjaxapu V，The application of automatic differentiation in the continuation power flow[C]．Proceedings of the Twenty-sixth Annual North American Power System Symposium． Manhatatten，KS， USA:Kansas State University，1994，pp．329－337．

[16]Orfanogianni T，Bacher R．Using automatic code differentiation in power flow algorithms[C]．IEEE transactions on Power Systems．1999:vol．14，no．1，pp．138 －144，Feb．

[17]Torres G L，Quintana V H．An interior point method for nonlinear optimal power flow using rectangular coordinates[C]．IEEE transactions on Power Systems．1998:vol．13，no．4，pp．1211 － 1218．