船用雷达ARPA中的自适应α－β滤波研究

冉元进 李 浩 李浩泷

(电子科技大学 成都 611731)

1 引言

船用雷达作为早期的海上航行辅助设备，在避碰上有很大的局限性。ARPA(Automatic Radar Plotting Aid，自动雷达标绘仪)的出现很大程度上提高了船用雷达避碰能力，减少了海上交通事故的发生。ARPA是通过识别、录取、跟踪目标的运动轨迹来实现避碰的，它是船用雷达功能的延伸。滤波跟踪作为ARPA处理目标信息最重要的环节决定着ARPA对目标的跟踪性能［1］。目前，研究较多的滤波跟踪算法有卡尔曼(Kalman)滤波、α－β滤波算法、粒子滤波、强跟踪滤波(STF)和交互多模滤波(IMM)等［2］。ARPA多采用简化的α－β滤波算法，这种简化方法对机动目标的跟踪性能较差［7］。

相对于传统雷达在极坐标系下做数据处理和显示，新型数字雷达的显示都要通过坐标变换，ARPA在研究船用雷达中增加了坐标变换的运算复杂度。若坐标变换后做跟踪滤波，则要求坐标变换后的数据在允许的误差范围内，同时要保证直角坐标系下的滤波跟踪性能与极坐标下的α－β跟踪滤波相当。本文采用一种直角坐标系下的自适应 α－β滤波算法。

2 α－β 滤波

2.1 传统ARPA中的α－β滤波

α－β滤波实际上是Kalman滤波的稳态解，因其简单可靠易实现被ARPA系统广泛采用。用简化α－β滤波所建立ARPA中匀速直线运动跟踪的模型如下［3，4，8］:

式(1)、(2)、(3)中sp(k)为第k－1个扫描周期预测的第k个周期的目标船与本船距离值;sm(k)为第k个周期距离的测量值;Sc(k)为第k个周期距离的计算值;α为距离平滑系数;vc(k)为第k个周期的速度，也即第k+1个周期的预测速度，β表示速度平滑系数。ARPA中α、β常用取值，α(k)=2(k－1)/［k(k+1)］，β(k)=6/［k(k － 1)］，这种滤波跟踪模型对匀速直线运动目标有很好的跟踪性能，但对机动目标的跟踪性能较差［3，4，6］。

2.2 极坐标下自适应α－β滤波

上面所述的简化α－β滤波模型主要针对匀速直线运动，极坐标下的自适应滤波跟踪是简化模型的延伸，它可以对机动目标进行跟踪。极坐标系下的目标位置由径向距离S和相对角度θ两个分量来表示，这里为了跟踪机动目标引入径向加速度aR(k)和角度加速度 aθ［10］。根据上述简化 α－β 滤波可描述极坐标下机动目标跟踪滤波方程如式(4)、(5)、(6)、(7)［3］:

传统雷达的滤波处理是在极坐标下完成的，新型数字雷达的显示要通过坐标变换，尤其在ARPA中直角坐标系下的滤波处理更为重要。

3 直角坐标系下的自适应 α－β滤波算法

滤波跟踪的准确性决定着ARPA避碰和显示的准确性，但是在考虑准确性的同时还需要考虑到处理器的运算速度能否达到要求。极坐标系下的自适应α－β滤的运算较为复杂，同时完成滤波后的数据还需要变换到直角坐标系下做显示处理，增加了坐标变换的运算量。现在提出一种先经过坐标变换，再在直角坐标系下来做滤波跟踪处理的思路，即直角坐标系下的自适应α－β滤波。这种方法在降低了滤波跟踪环节运算量的同时，还降低了坐标变换环节的运算量，并能实现机动目标的跟踪。下面具体分析该算法的处理过程。

3.1 坐标变换与数据稳定性

在坐标变换后做滤波跟踪处理，要满足一个前提条件，就是坐标变换前后数据没有大的差异。以本船为坐标原点建立坐标系，极坐标用(S，θ)表示，直角坐标用(x，y)表示，则坐标变换可以由式(8)和式(9) 表示［9］。

3.2 直角坐标系下的α－β滤波算法

根据传统方法和极坐标系下的自适应α－β滤波算法，在直角坐标系下建立自适应α－β滤波的运动模型。工程常用的α、β计算方法精度和自适应性较差，在直角坐标系模型中采用一种残差累积法来计算α、β的值以提高跟踪滤波自适应能力。直角坐标系中x方向上的滤波由式(10)～(12)表示，y方向上的滤波由式(13)～(15)表示:

这里的滤波方程同传统ARPA中α－β跟踪滤波方程相似，xp(k)代表第k－1个周期预测的第k个周期目标船的横坐标值;xm(k)代表第k个周期目标船横坐标的测量值，xc(k)代表第k个周期目标船横坐标的计算值;vx(k)第k个周期x方向上的速度分量;ax(k)代表第k个周期x方向上的距离平滑系数，βx(k)代表第k个周期x方向上速度分量的平滑系数。同理，y轴上的各个分量与x方向上的分量含义相同。

α、β修正系数的引入是因为数据的测量和预测存在随机误差。若将其设置为固定值，或按照传统方法去计算，一旦目标发生机动就很容易丢失。为了增强α－β滤波的自适应能力，采用一种残差累积滑动法来计算α、β的值。预测误差方差，即残差用表示，测量误差方差用示。预测误差有累积的过程，需要设立一个长度为3～6的滑动窗来不断更新即 为预测误差均方根;是雷达设备的固有误差，通常为恒定值。下面以x方向上的α、β值的计算为例来具体说明［4，6］。

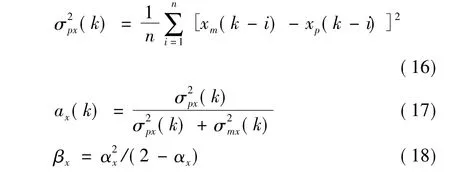
机动目标跟踪外推方程:

外推方程式(19)～(24)主要用于机动目标的跟踪处理，这里只要将外推的机动目标各坐标轴上的预测值带入式(10)、式(13)中即可得到机动目标的跟踪值。

4 性能比较与分析

用MATLAB模拟目标航船初始运行状态和机动过程及后续运行状态。目标运动过程可描述为先做匀速直线运动，到131个扫描周期时发生机动，机动后仍做匀速直线运动。当雷达脉冲的采样点数设定为1024，雷达量程设定为12km时，两个采样点之间代表的距离为12/1024km。那么根据表1所示的目标匀速直线运动和机动后的相关参数，目标运行速度可换算成10.29m/s和7.92m/s。表1中x、y分别代表用采样点表示的目标航船的横纵坐标位置。径向距离和角度参数可根据表1运算出的x、y表示为和 θ=arctan(y/x)，并对得到的距离和角度参数取整。再用取整得到的极坐标参数做坐标变换，这里存在近似取值，主要是因为采样点数有限的缘故。

表1 目标运动状态

把得到的径向距离和角度参数代入式(1)～(7)做极坐标系下的滤波跟踪处理，求得预测误差再代入式(16)求极坐标系下的预测误差均方根;将坐标变换后得到的x、y参数代入式(10)～(24)做直角坐标系下的滤波跟踪处理，并求直角坐标系下的预测误差均方根。最后将直角坐标系下的均方误差转换为极坐标系下的均方误差进行比较。

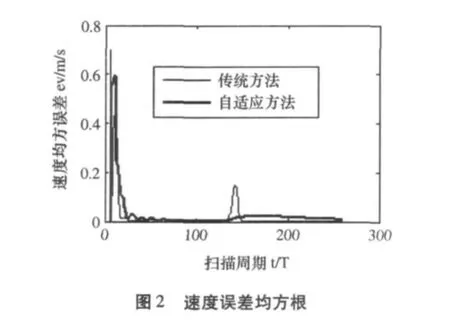
图1中比较了传统方法和自适应方法下的距离误差均方根。匀速直线运动部分两种方法的距离均方误差相近都低于10m;第131个扫描周期时目标发生机动，此时传统方法不能继续跟踪，而直角坐标系下的自适应方法在机动后的30个扫描周期内仍可建立起稳定的跟踪。图2表明两种方法速度均方误差都在0.02m/s左右，自适应方法跟踪精度略优于传统方法。图3比较了两种方法下的角度均方误差，自适应方法角度跟踪精度优于传统方法，均方误差低于0.1°。因此，ARPA系统中采用直角坐标系下的自适应滤波方法能够很好的实现匀速直线运动目标和机动目标的自适应跟踪。

5 结论

本文针对船用雷达ARPA系统中α－β滤波对机动目标跟踪性能较差，同时坐标变换计算量较大的问题，提出了ARPA系统中运用直角坐标系下的自适应α－β滤波算法。经过Monte-Carlo仿真验证了直角坐标系下的自适应滤波对ARPA中匀速直线运动目标的跟踪精度优于传统方法，并且对机动目标有较好的跟踪能力。

［1］Liu Xiuwen，Yin Yong，Jin Yicheng，Zhang Xinyu.Design radar signal interface for navigation radar/ARPA simulator using radar display［J］.IEEE Second Pacific-Asia Conference on Circuits，Communications and System(PACCS)，2010，442 －445.

［2］兰剑，慕春棣.基于参考加速度的机动目标跟踪模型［J］.清华大学学报，2008.

［3］许录平.跟踪机动目标的自适应α-β滤波算法［J］.西安电子科技大学学报，1998，25(3).

［4］王红亮，李枫，赵亦工.一种机动目标跟踪的自适应α－β滤波算法［J］.雷达科学与技术，2008，(4).

［5］刘长江，袁俊泉，马维嵘，丁顺宝.径向速度量测在机动目标跟踪中的应用［J］.现代雷达，2010，32(6):31 －34.

［6］李良群，谢维信，黄敬雄，廖桂生.非均匀稀疏采样环境自适应α-β滤波算法［J］.系统仿真学报，2009，21(16):5138 －5140.

［7］吴建华.自动雷达标绘仪(ARPA)［M］.武汉理工大学出版社，2009.

［8］赵星，李明，吴顺君.混合坐标系下的自适应α-β 滤波［J］.火控雷达技术，2005，34(1):13－16.

［9］李宏波，李浩，张可.基于FPGA的脉冲雷达成像研究与实现［J］.火控雷达技术，2011，40(3):61－64.

［10］江桥，罗利强.伪加速度修正自适应α-β滤波算法研究［J］.火控雷达技术，2005，34(2):9－13.