多元多峰值目标函数在MATLAB中的优化
2012-09-29姚运萍王倩倩
姚运萍 ,王倩倩
(1.兰州理工大学 数字制造技术与应用省部共建教育部重点实验室,甘肃 兰州730050;2.兰州理工大学 机电工程学院,甘肃 兰州730050)
多元多峰值函数[1-2]在定义域内有多个局部极值点,许多传统的优化方法都是单点搜索,这种点对点的搜索方法,对于多元多峰值函数的搜索空间常常会陷入局部的某个单峰的极值点。相反,遗传算法同时对群体中多个个体进行并行处理[3],即同时对搜索空间中的多个解进行评估,在搜索过程中能以很大的概率找到全局最优。遗传算法提供了一种求解非线性、多模型、多目标等复杂系统优化问题的通用框架,它不依赖问题领域的具体性,已广泛应用于众多工程领域,用以解决多变量、多目标、多峰值等约束的优化问题。
1 遗传算法
1.1 遗传算法的优点
(1)遗传算法采用不确定性规则,强调利用概率转换规则[4]来引导搜索过程;
(2)遗传算法随机产生多个初始点,通过选择、交叉和变异三种遗传操作产生下一代种群;(3)遗传算法具有较高的搜索能力和极强的鲁棒性;(4)遗传算法采用概率的变迁规则来指导其搜索方向[5],对一个被编码的参数空间进行高效搜索;
(5)遗传算法是一个多学科相结合与渗透的产物,其研究方向极其广泛。
1.2 遗传算法运算流程
完整的遗传算法的运算流程可以用图1来描述。可以看出,使用上述三种遗传算子(选择、交叉和变异)的遗传算法的主要运算过程如下:
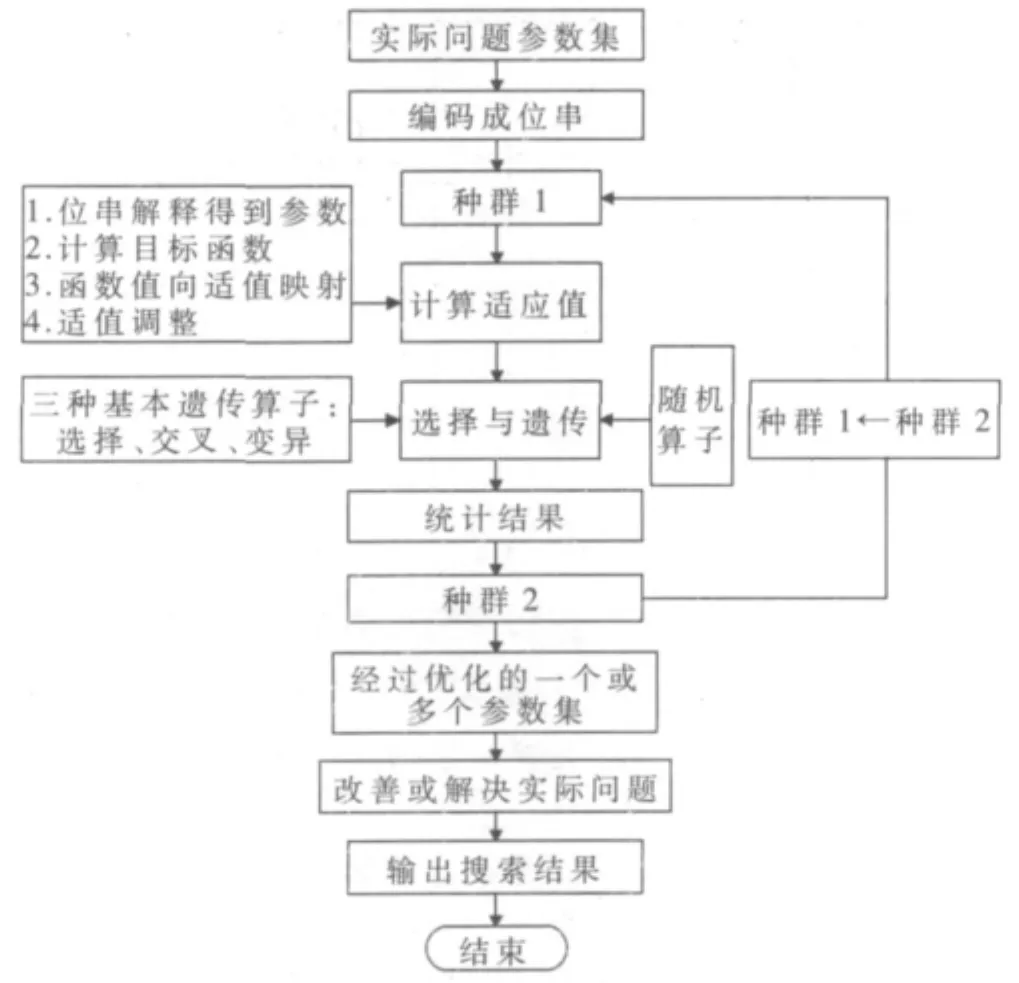
图1 遗传算法运算流程图
(1)编码:遗传算法在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合就构成了不同的点。
(2)初始群体的生成:随机产生N个初始串结构数据,每个串结构数据成为一个个体,N个个体构成一个群体。设置进化代数计算器t(t>0)和最大进化代数T。
(3)适应度值评价检测:根据具体问题,计算群体P(t)中各个个体的适应度。
(4)对群体中的个体施加遗传操作:将选择、交叉和变异三种遗传算子作用于群体,实现群体内个体结构的重组处理。
(5)终止条件判断:若 t≤T,则 t←t+1,转到步骤(2);若t>T,则以进化过程中所得到的具有最大适应度的个体作为最优解输出,终止运算。
2 基于MATLAB遗传工具箱的多元多峰值优化
遗传算法工具箱使用MATLAB矩阵函数为实现广泛领域的遗传算法建立了一套通用工具,这个遗传算法工具是用M文件写成的命令行形式的函数,是完成遗传算法大部分重要功能的程序集合[6-8]。
MATLAB遗传工具箱主要参数含义:
(1)“@fitnessfcn”:计算适应度函数值的M文件的函数句柄;
(2)“nvars”:适应度函数中独立变量的个数;
(3)“x”:最终值的到达点;
(4)“fval”:适应度函数在 x 点的值;
(5)“reason”:算法停止的原因(可选项);
枢纽锚固是在对外客运枢纽布局的基础上,充分发挥城市交通网络的功能,如道路、轨道交通等。在对外客运枢纽设计中,发挥锚固区域交通网络的作用,如高速公路、干线公路、城际公路、铁路以及公路客运班线等。因此,城市综合客运枢纽的锚固能够为人民群众出行的便捷性提供保障。
(6)“output”:包含关于算法在每一代性能的结构体(可选项);
(7)“population”:最后种群(可选项);
(8)“option”:一个包含遗传算法选项参数的结构体(可选项)。
如果不设置选项函数,则遗传算法使用其本身自带的缺省选项值。该参数结构体的自带默认值分别为:种群规模为 20,最大代数为 100,选择概率为 0.8,交叉概率为0.5,变异概率为0.2。也可通过gaoptimset函数改变默认值,以达到使用者的需求。
3 多元多峰值函数优化实例
目标函数及函数的约束条件:
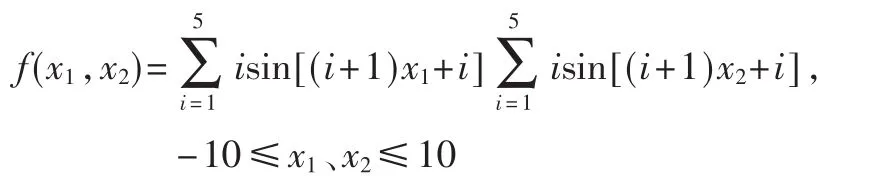
图2所示为目标函数的函数图像。

图2 目标函数图像
遗传算法显示结果如下:
(1)经过10次迭代后的目标函数值如图3所示。此时,x1=-6.785 1,x2=-7.426 8,minf(x)=-176.621 1。
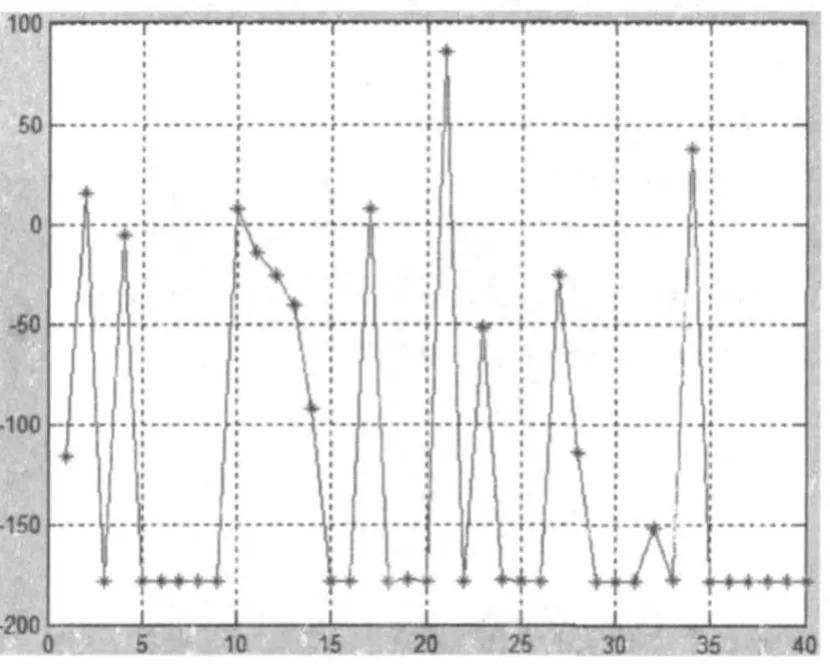
图3 经过10次迭代后的结果
(2)经过50次迭代后的目标函数值如图4所示。此时,x1=-6.774 6,x2=-7.397 3,minf(x)=-178.519 1。
(3)经过50次迭代后,种群目标函数均值的变化和最优解的变化如图5所示。
本文采用基于MATLAB的遗传算法,利用强大的数学计算能力和遗传工具箱,在全局搜索空间内寻找极值点,能够有效地对多元多峰值函数进行优化,避免了利用传统优化方法在多元多峰值函数优化过程中陷入局部极值点的优化误区。使用者可以避免维护遗传算法种群和染色体的数据结构的繁重编程工作,节省了大量编程时间和精力,将精力集中在遗传算法的改进和具体问题的应用中。
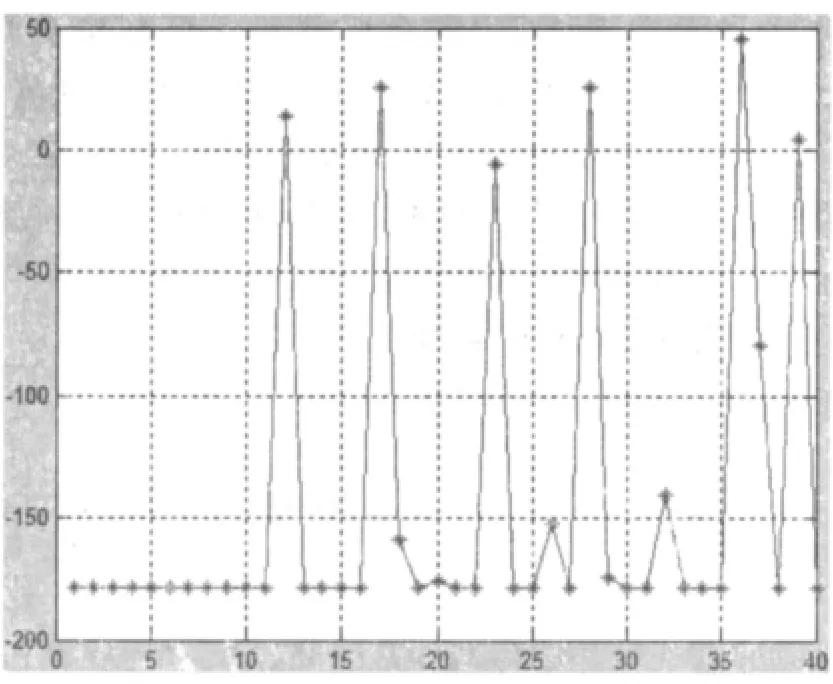
图4 经过50次迭代后的结果
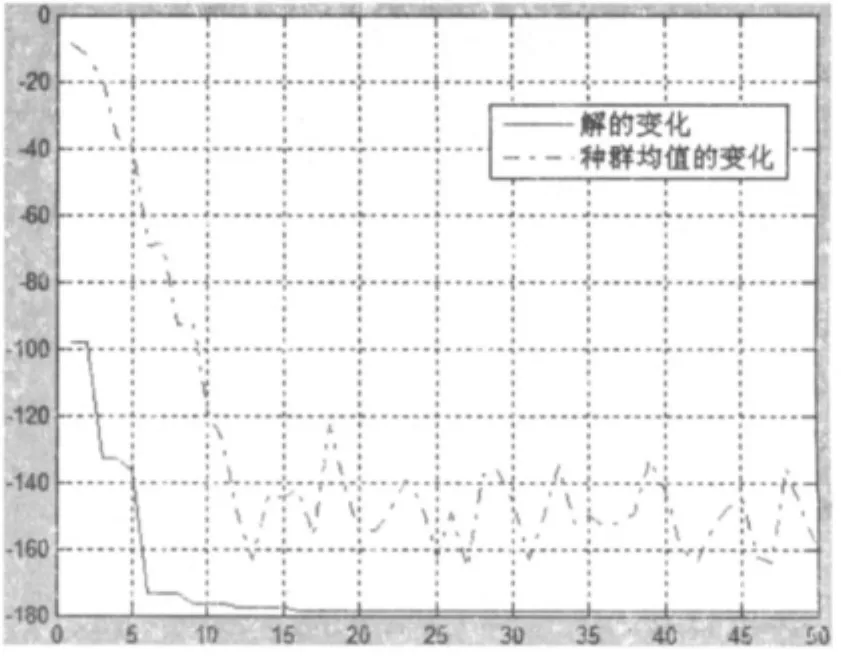
图5 经过50次迭代后种群目标函数均值的变化和最优解的变化
[1]李敏强,寇纪淞,林丹,等.遗传算法的基本理论与应用[M].北京:科学出版社,2003.
[2]孙小军,赵天绪,焦建民.多峰极值优化问题的算法性能分析和比较[J].昆明理工大学学报(理工版),2009,34(5):104-107.
[3]刘道华,原思聪,邬长安,等.面向对象的改进遗传算法优化设计[J].华中科技大学学报(自然科学版),2008,36(7):89-92.
[4]张晓伟,刘三阳,迟晓妮.高效求解多峰值全局优化的区间-遗传算法[J].吉林大学学报(工学版),2008,38(4):876-879.
[5]黄江波,付志红.基于自适应遗传算法函数优化与仿真[J].计算机仿真,2011,28(5):237-240.
[6]雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.
[7]刘文强,张晓伟.多峰值全局优化的混合算法[J].计算机工程与应用,2008,44(3):43-45.
[8]王社科.机械优化设计[M].北京:国防工业出版社,2007.
