干扰源双星定位中的邻星同频干扰解调对消方法

杨宇翔,夏畅雄,熊瑾煜,陈 鲸

(盲信号处理重点实验室,成都610041)

1 引 言

干扰源双星定位系统中,需要有能够接收到干扰辐射源旁瓣信号的邻星,而在目标信号同频段上存在着邻星的正常通信信号是十分常见的,使得本来就很微弱的目标信号又多了一个很强的干扰,导致信噪比过低,时差、频差定位参数无法提取,定位处理更是无从谈起,严重制约了双星定位系统的作用和效益。所以,必须对干扰信号进行抑制,或者说将目标与干扰信号从混合信号中分离开来。

目前,这种时频混叠的单通道信号分离的研究刚起步不久[1],它是欠定盲信号分离[2]中一种比较极端的情况。针对不同的应用实例,已有文献尝试利用信号分量间的参数差异来实现分离:如利用时延差异的过采样解相关算法[3];利用成形滤波差异的过采样多通道分离方法[4-5];文献[6]则利用小波变换对符号速率存在微小差异的混合信号进行分离。然而,过采样解相关算法需知晓各信号的成形波形,连续帧估计时误差存在累积效应,且涉及矩阵求逆,计算复杂。过采样多通道分离方法只能应用在信号成形脉冲差异较大且信噪比较高的场合,并且上述两种方法只适用于信号分量符号速率相同的情况。而小波变换法利用符号速率的微小差异构造小波变换实现分离,但对于非矩形脉冲成形时其性能急剧下降,当归一化低通带阻系数在0.20以下时基本上不能实现分离。可见,上述方法在应用中存在较大局限,只有在满足特定要求下才能进行分离,难以适应信号的复杂多变。为此,本文重点突破了信号幅度、相位、时延的实时估计和跟踪调整等关键技术,结合调制识别、信号参数估计以及解调技术,提出了一种基于解调对消的干扰抑制方法,通过重构出干扰信号,再用混合信号与之相减,达到分离目标和干扰信号的目的。该方法充分利用了邻星干扰与目标信号功率差异较大的特点,在双星定位的应用场景下能够获得较好的干扰抑制效果。

2 同频干扰信号解调对消方法

2.1 信号模型

高斯信道下,如果主星接收的信号表示为

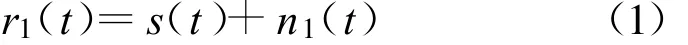
则接收到的邻星信号可以表示为

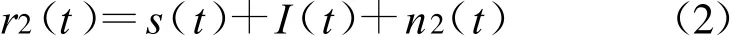
式中,s(t)为目标信号,I(t)为干扰信号,传统的同步卫星通信一般采用常规调制信号,其调制方式通常为BPSK、QPSK、8PSK和16QAM 中的一种,故下面的讨论中,主要针对这4种调制方式进行,n(t)为高斯白噪声。

考虑复基带模型,干扰信号可以表示为

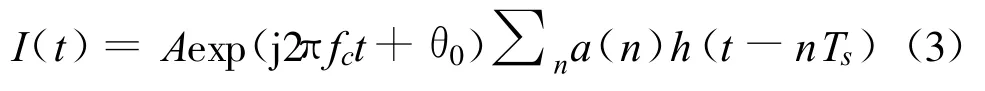
式中,A为干扰信号的幅度,fc为载波频率,θ为载波初相,a(n)为发送的码元,干扰信号为MPSK调制时 ,a(n)=ej2πi/M;i=0,1,2,…,M-1;16QAM时,a(n)=c+jd;c,d=2i-15,i=0,1,…,15。Ts为符号周期,h(t)为等效信道滤波器,由于卫星通信信道较为理想,一般采用升余弦滤波器代替即可。可见,在没有任何先验信息的前提下,要重构干扰信号I(t),必须对上述所有参数进行估计。

2.2 信号参数估计

干扰信号码速率和载波的估计是调制方式识别和解调的基础,可通过MPSK、16QAM的包络频谱和倍频谱估计符号速率和信号载波。

(1)符号速率估计

对于式(3)所示的复基带形式的干扰信号,其信号包络谱的定义如下:

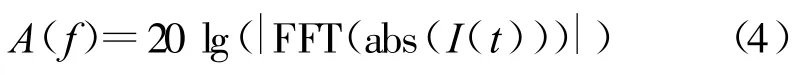
由于调制类型为MPSK或16QAM方式的干扰信号均可由两路正交信号合成(因为 ej2πi/M=cos(2πi/M)+jsin(2πi/M)=an+jbn),则干扰信号可以表示为

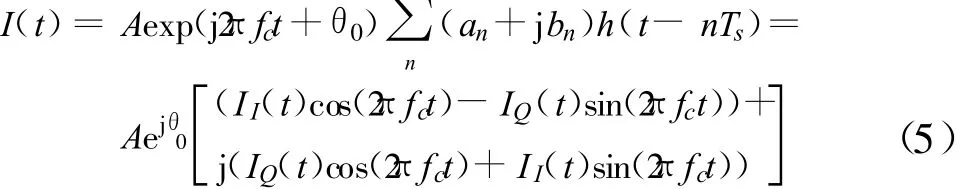
而

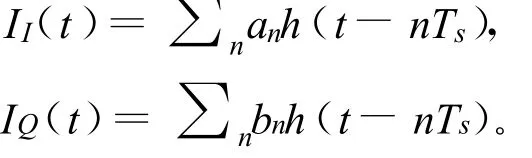
an、bn满足以下条件:当 n≠m时,E(anam)=E(bnbm)=0。另由于目标信号非常微弱,可忽略其对干扰信号复包络的影响,因此邻星混合信号的包络平方为

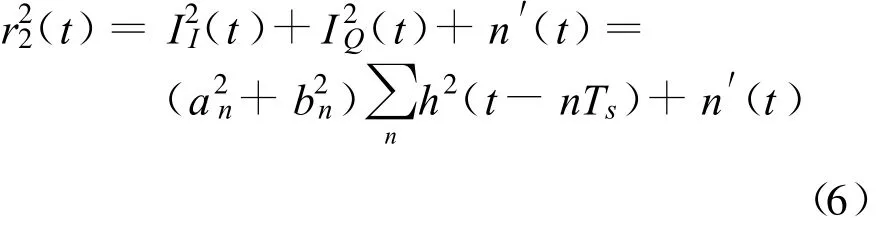
式中,n′(t)为噪声和白噪声项,由于干扰信号I(t)是邻星上的正常通信信号,其信噪比较高,对式(6)表达的包络平方作傅里叶变换可得

式中,H(f)是 h(t)的傅里叶变换。因此对MPSK、16QAM信号的包络求频谱会出现符号速率的整数倍单频分量,故只需搜索复包络频谱R(f)上的第一个单频波峰,即为信号的符号速率Rs。

(2)载波估计

由于BPSK信号在其平方谱上有2倍载波的离散谱线,QPSK、16QAM在其四次方谱上也含有4倍的离散谱线,而8PSK信号的8倍载波离散谱线在其八次方谱上表现出来,故可以利用此特征对干扰信号的载波进行估计。

通过上述方法估计符号速率和载波频率时,其估计精度有时仍不能满足需求,为进一步提高精度,可利用Zoom-FFT对估计结果的附近区域进行频率细分,提高计算分辨率后作更精确的估计,以满足后续识别、解调的需求。

2.3 调制方式识别

干扰信号主要为MPSK和16QAM,依据信号倍频特征便可首先区分BPSK和8PSK,因为它们分别会在平方谱和八次方谱出现离散谱线;而四次方谱上有离散谱线时,还需要进一步区分是QPSK还是16QAM调制方式。此时,根据幅度平坦度系数的大小便可区分,幅度平坦度系数也称为 R参数,其定义为信号包络平法的方差与均值的平方之比,用于描述瞬时幅度起伏情况。由于16QAM的瞬时幅度在3个值之间变化,从而R参数较大;而QPSK作为调相信号,在幅度上不携带信息,只是由于成形滤波和相位变化对波形的影响,在瞬时幅度上有很小的波动,故其R参数较小。需注意的是BPSK信号虽然在幅度上不携带信息,但相位反转会引起波形突变,加之成形滤波的影响,其瞬时幅度波动也较大。这4种调制方式的倍频和R参数特征如表1所示。

表1 4种调制方式的参数特征Table 1 Parameter characters of four modulation types

由表1可见,4种调制方式的参数特征各不相同,因此能够以此完成调制方式的识别。

2.4 信号解调

作为邻星上的正常通信信号,干扰信号的功率较强,且目前MPSK、MQAM解调技术已经十分成熟,这里就不作描述了。

2.5 重构对消

在完成了前面的步骤后,就得到了干扰信号的调制方式、载波、码速率 Rs和解调得到的码元a(n)。利用这些信息进行重新调制,就得到了初步的参考信号。此时,参考信号与干扰信号的差异就主要在于样点时间未同步、幅度和初相的不同了。

2.5.1 样点时间同步

由于信号采集时的采样率与码速率往往不是整数倍的关系,而信号重新调制时,每个码元对应的样点数只能为整数,则参考信号每个码元对应的样点数与干扰信号不一致。随着观测时间的增长,码元个数的增加,参考信号和干扰信号间的样点将出现明显的错位,导致同一时刻两者的样点不是一一对应的关系,严重会影响后续的初相、幅度差异的估计,导致最终重构出的样本信号与干扰信号差异巨大,达不到预期的抑制效果。

为此,首先根据采样率与估计的码速率的比例关系对参考信号进行重采样,确保参考信号每个码元对应的样点数与干扰信号基本相同。其次,将信号进行分段处理,依次将干扰信号和参考信号分段相关,得到两段信号间的延迟样点数,并据此将参考信号在时域上进行滑动,确保其与真实干扰信号的每个样点尽量对齐。

2.5.2 相位与幅度差异的补偿

当参考信号与干扰信号的样点基本对齐后,由于解调码存在相位模糊,并且重新调制时,信号的幅度和初相是未知的,故需要对参考信号的相位和幅度进行调整,这就涉及到了参考信号与干扰信号间幅度和初相差异的估计。

类似于式(5),参考信号C(t)的表达式为

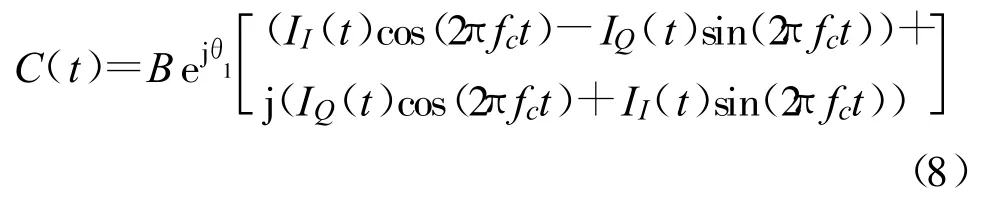
式中,B和θ1为参考信号的幅度和初相,其他参数如载波、码元等假设均与干扰信号相同,将混合信号和参考信号进行互相关计算,取其零点可得

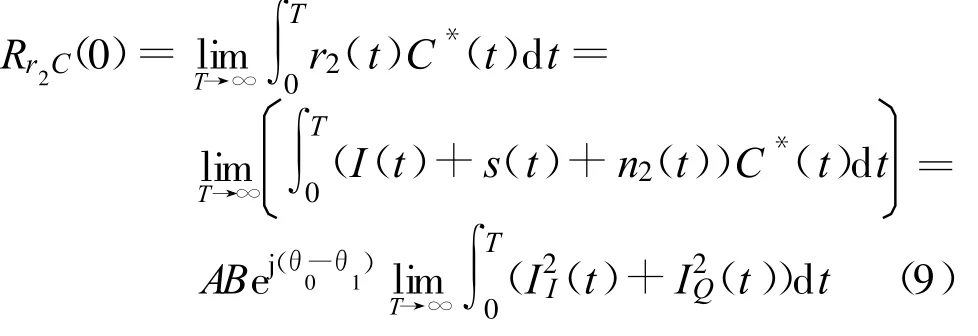
忽略目标信号和噪声的功率,对混合信号作自相关运算可得

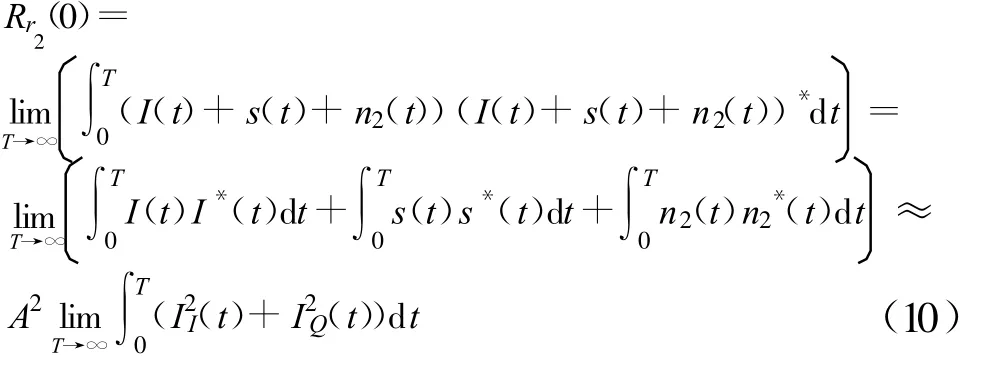
同理,可得

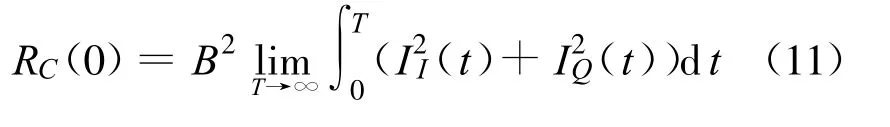
故相位差的估计表达式为

也可得到参考信号与干扰信号幅度的比例关系:

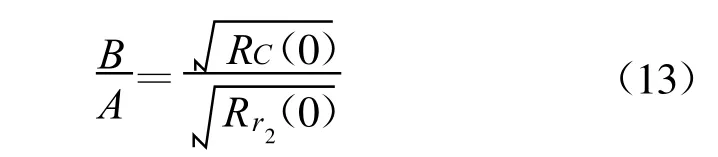
根据式(12)～(13)估计出参考信号与干扰信号的幅度、相位差异对参考信号做进一步的调整,得到了与干扰信号基本相同的样本信号,用混合信号与之相减后,就实现了干扰信号功率的削弱,达到了抑制干扰的目的。

综上所述,本文的干扰抑制方法流程如图1所示,具体步骤如下:

(1)首先估计出干扰信号的载波、码速率;

(2)识别干扰信号的调制方式;

(3)对干扰信号进行解调;

(4)根据识别的调制方式和估计的载波、码速率重新对解调得到的码元进行调制,得到参考信号;

(5)估计并补偿参考信号与干扰信号的幅度和相位差异,得到最终的样本信号;

(6)用混合信号减去样本信号,抵消干扰信号的功率,提高目标信号的信噪比;

需要注意的是,上述流程并非是完全串行的,可在解调得到一定数量码元后就开始估计并补偿相位和幅度的差异,形成样本信号,同时用混合信号与之相减。这样,信号解调完成的时候,干扰信号的抑制工作也基本完成,同时还能对干扰信号进行分段并行处理,以进一步提高处理速度。

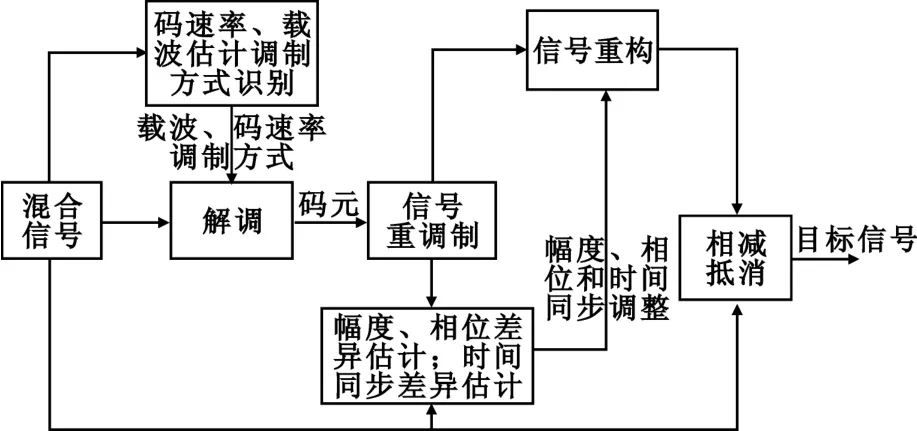
图1 抑制方法流程图Fig.1 Flowchart of restrainmethod

至此,参考信号与干扰信号各参数的差异均已完成补偿。但由于噪声的存在,各项参数的估计均存在误差,导致最终得到的样本信号与干扰信号并非完全一致,也即抑制后,仍存在干扰信号的残余量。文献[7-9]均以干扰抑制比来评价干扰抑制的性能,并分析给出了干扰抑制比ρ与归一化幅度估计方差、载波相位估计方差、归一化符号定时估计方差σ2t以及误码率Pe的关系:

其中,γ与调制方式有关,如调制方式为BPSK时 γ=4,QPSK时γ≈2,等;β为信道脉冲响应的归一化均方根带宽。

3 仿真分析

图2给出了本文所提出的方法在不同误码率条件下的干扰抑制性能。从图中可以看出仿真和计算结果基本一致,说明本文方法有着较好的性能,能够逼近理论下界。

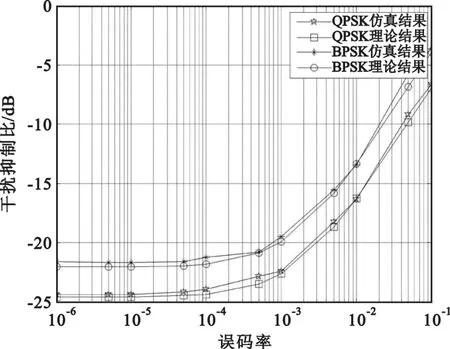
图2 性能曲线Fig.2 Performance curve vs BER

此外,为验证该方法对定位参数获取的作用,产生与邻星目标信号存在时频差的主星信号,信噪比为10 dB,其他条件不变,选取干扰信号的调制方式为QPSK,误码率为10-6时的情况进行仿真:解调对消之前,由于邻星上干扰强,将主邻星数据进行互模糊函数计算后,无法检测到峰值,如图3所示。利用本文方法处理后,得到了如图4所示的抑制前后的功率谱,圆圈表示抑制前,米字表示抑制后信号。由图对比可见,干扰信号功率明显削弱了。再重新计算互模糊函数,得到如图5所示的结果。

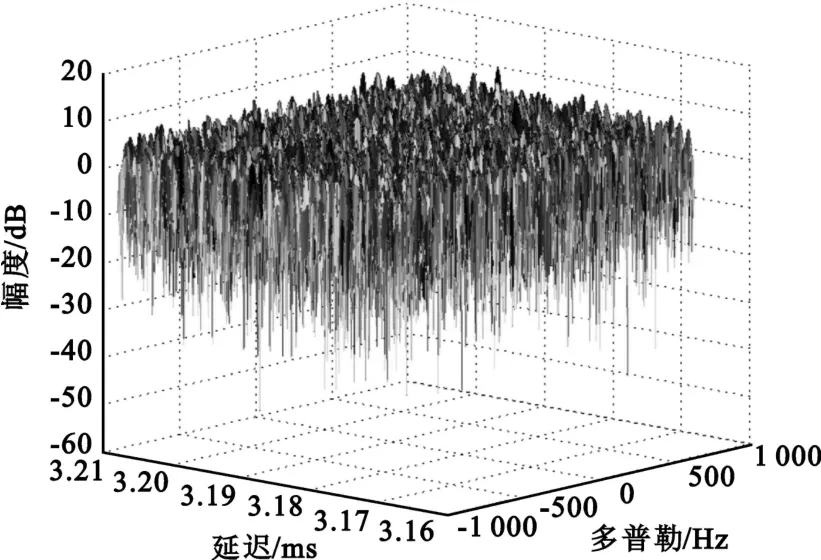
图3 对消前互模糊函数结果Fig.3 Result of CAF before cancellation

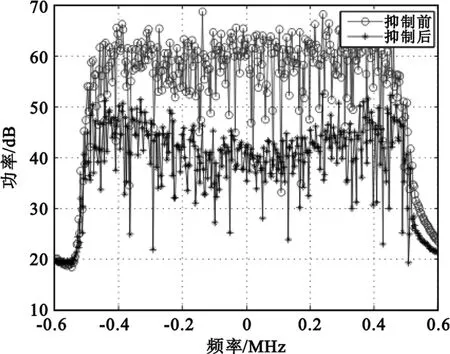
图4 对消效果Fig.4 Effect of cancellation

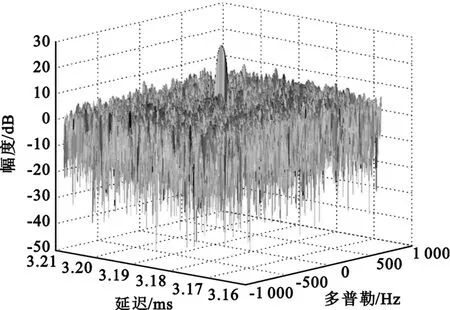
图5 对消后互模糊函数结果Fig.5 Result of CAF after cancellation

可见,经过解调对消抑制处理后,有效地提高了邻星目标信号的信噪比,同样的处理增益下,原本淹没在噪声中的相关峰突显出来。表明本文方法在实现干扰信号功率抑制的同时,并未对与之混叠的微弱目标信号造成破坏,能够有效解决同频干扰条件下的定位参数估计问题。

4 结束语

本文提出了一种基于解调对消的同频干扰抑制方法,该方法相比其他单通道信号分离技术而言,充分利用了双星定位系统中邻星干扰与目标信号功率差异较大的特点,更具有针对性,能够有效抑制邻星的同频干扰,解决参数无法估计的问题。值得注意的是,此方法应用于其他场景时,由于信道可能存在畸变,需在波形重构后完成信道的估计与补偿,再进行抵消。此外,本文方法具备了并行处理的特点,可对混合数据进行分段,再利用GPU、FPGA等实现并行处理,以进一步提高算法的时效性,具备工程实用价值。

[1]彭耿,黄知涛,姜文利,等.单通道盲信号分离研究进展与展望[J].中国电子科学研究院学报,2009,4(3):268-277.PENG Geng,HUANG Zhi-tao,JIANG Wen-li,et al.Development and perspective of single channel blind signal separation[J].Journal of China Academy of Electronics and Information,2009,4(3):268-277.(in Chinese)

[2]Li Yuan-qing,Amari S,CichockiA,et al.Undeterminedblind source separation based on sparse representation[J].IEEE Transactions onSignal Processing,2006,54(2):423-437.

[3]Brandt P M.Signal separation using fractional sampling in multiuser communications[J].IEEE Transactions on Communications,2000,48(2):242-251.

[4]Zhang Yinglu,Kassam S A.Multichannel blind source separation and blind equalization using fractional sampling[C]//Proceedings of the second InternationalWorkshop onIndependentComponent Analysis and Blind Signal Separation.Helsinki,Finland:IEEE,2000:285-289.

[5]Warner E S,Proudler I K.Single-channel blind signal separation of filtered MPSK signals[J].IEE Proceedings Radar,Sonar and Navigation,2003,150(6):396-402.

[6]Heidari S,Nikias C L.Co-channel interference mitigation in the time-scale domain:the CIMTS algorithm[J].IEEE Transactions on Signal Processing,1996,44(9):2151-2162.

[7]潘申富,李振东,梁庆林.参数估计误差对串行干扰抵消性能的影响[J].电波科学学报,2004,19(1):17-20.PAN Shen-fu,LI Zhen-dong,LIANG Qing-lin.Performance degradation caused by imperfect parameter extraction in serial interference cancellation[J].Chinese Journal of Radio Sci-ence,2004,19(1):17-20.(in Chinese)

[8]李峰,潘申富,路建平.串行干扰抵消器性能分析[J].无线电工程,2005,35(5):1-2.LI Feng,PAN Shen-fu,LU Jian-ping.Performance analysis of serial interference cancellation[J].Radio Engineering of China,2005,35(5):1-2.(in Chinese)

[9]田文科,王剑,山秀明.PCMA自适应干扰对消算法与仿真[J].电讯技术,2011,51(9):78-82.TIAN Wen-ke,WANG Jian,SHAN Xiu-ming.Adaptive interference cancellation for paired carrier multiple access[J].Telecommunication Engineering,2011,51(9):78-82.(in Chinese)