考虑地震动不确定性的核电厂楼层反应谱分析
2012-09-28林皋,李建波,钟红,胡志强
林 皋, 李 建 波, 钟 红, 胡 志 强
(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;2.大连理工大学 建设工程学部,辽宁 大连 116024)
0 引 言
我国核电建设中的自主化程度不断提高,许多设备实现了国产化生产.这就要求对不同地震地质环境中的复杂地基上的核电厂结构进行地震响应分析,作为核岛厂房结构和设备抗震安全评价的依据.其中楼层反应谱更受到关注,因为它构成设备抗震适应性评价的主要内容,同时也是赖以确定是否要对厂房结构采取必要减振措施以保障设备抗震安全性的重要指标.
当前,核电建设中比较普遍采用的是确定性的分析方法.实际上,地震的发生具有明显的随机性,地震强度和频谱特性具有很大的不确定性.本文的目的在于参考美国ASCE《核电厂设备结构分析与设计手册》所建议的Monte Carlo随机样本模拟法[1],提出地震动不确定性的计算模型,建立样本空间,然后通过对数值结果的数理统计,获取不用置信率的响应分析结果.这样可对传统确定性设计方法获得的动力响应计算结果进行置信率的定量判断,以便对其保守程度作出恰当评价,加深对核电结构安全性的认识.
核电厂结构地震响应或楼层反应谱的特点是共振峰十分尖锐,尤其对小阻尼的情况表现得更为突出.只要激励频率稍许偏离共振频率,其动力放大系数就将显著地降低.而共振频率的确定本身就含有较大的不确定性.所以,许多国家的核电抗震规范,例如,美国的ASCE4-98就规定,为了考虑参数不确定性的影响,建议将按确定性方法所计算出的楼层反应谱适当拓宽.考虑地基剪切模量不确定性的影响时,建议峰值的拓宽范围不小于±15%.当位于峰值频率附近的结构子系统的数量不止一个时,也可采用峰值移位的方法[2].通过研究还发现,考虑参数不确定性影响后,楼层谱不仅在峰值部位拓宽变胖,同时峰值还有所下降.ASCE4-98规定,在阻尼比小于10%的情况下,在峰值拓宽的同时容许将共振峰值削减15%左右,对于小阻尼的情况,实际上峰值下降的幅度还要更大.为此,ASCE4-98规定,在经过充分论证的前提下,只要保证不超越的概率不会低于90%,峰值的降低幅度可不受15%的限制.
本文将采用概率统计的方法结合我国地震动的特点,研究地震动的不确定性对核电厂楼层反应谱的影响,暂不考虑地基和结构参数不确定性的影响.据作者所知,反映核电厂运行期内输入地震动的不确定性对结构地震响应的影响的定量评价研究尚未见有文献报道.美国ASCE《核电厂设备结构分析与设计手册》提出了应用Monte Carlo方法进行地震动不确定性分析的观点,但没有提出反映地震动不确定性的累积曲线或概率密度分布曲线的构造方法.本文的研究将加深对核电厂抗震设计风险程度的了解,并将促进核电厂确定性分析向性能设计方向的发展.
1 地震动输入不确定性的研究
地震荷载的不确定性是核电厂设计中一项重要的不确定性来源,而厂址地震动的不确定性又是一个需要研究和探索的问题.根据研究和体会,本文提出以下方案来考虑厂址地震动不确定性的影响.
厂址输入地震动的不确定性取决于厂址的地震地质条件,这和厂址周围潜在震源区的地震活动性、地震动的衰减关系以及厂址的局部地形地质条件相关,有很强的个别性,但仍然有规律可循.目前,国内外的抗震设计都普遍接受反应谱理论,以反应谱来表征地震动的特性.工程设计上常用加速度反应谱,以加速度大小表示地震作用的强弱.以反应谱的形状,即加速度放大系数随结构频率(或周期)的变化来反映潜在震源区震级大小、距离远近以及工程厂址地质条件对地震动特性的影响.核电工程由于其特殊的重要性,往往进行专门的厂址地震安全性评价,给出峰值地震加速度的超越概率曲线,据此可以进行地震作用强弱的不确定性分析.地震安评报告中虽然也同时给出了建议的厂址设计反应谱形状,但那是一致概率反应谱,相对比较保守,过高估计了设计地震中的长周期成分,它不是地震环境下真实样本的实现,从而造成重大工程结构抗震设计上的困难.所以,这种一致概率反应谱并不为一般工程设计所采用.工程上采用较多的是在强震记录统计分析基础上所获得的标准反应谱,如我国国标《建筑抗震设计规范》[3]所提出的反应谱,《核电厂抗震设计规范》[4]所推荐的反应谱以及核电工程设计中所常用的RG1.60谱等.影响反应谱形状的因素很多,也很复杂.目前还缺乏必要和充分的资料来研究反应谱形状不确定性的影响.所以,建议采用确定性的反应谱形状,亦即通过大量实测的强震记录统计分析得到的反应谱,这样比较接近实际.可采用统计平均反应谱,也可采用平均值加1倍标准差的反应谱,则所得结果偏于保守,也偏于安全.
我国具有丰富的历史地震资料,为地震动强度的不确定性分析提供了重要的依据.但是限于当时条件,历史地震只能采用烈度,即地震所造成的灾害性后果来评价地震动的强弱.根据我国主要地震影响区域内(包括华北、西北、西南、新疆等地区)地震发生概率的统计分析[5],在一般建筑物规定的50a运行基准期内,其烈度的概率分布大致如图1所示.规范规定的场地基本烈度相当于中震,其超越概率为10%~13%;众值烈度相当于小震,其超越概率为63.2%;罕遇烈度相当于大震,其超越概率为2%~3%.将烈度按规范换算为相应加速度(表1)后,可以获得不同烈度区内地震加速度的年累积超越概率曲线.各核电厂的安评报告也提供了相应厂址的地震加速度年超越概率曲线,图2中所示为某一厂址的年超越概率(Pe)曲线.其分布规律与我国7度区、8度区和9度区的分布规律是相似的.从而可据此进行地震动强度的不确定性分析.

图1 我国主要地震影响区烈度超越概率Fig.1 Probability of exceedance for seismic intensity of seismic active areas in China

表1 不同烈度区加速度峰值取值Tab.1 Peak acceleration of area with different seismic intensities

图2 输入地震加速度的年超越概率曲线Fig.2 Annual probability of exceedance for the seismic input acceleration
由年超越概率曲线即可求得建筑物50a运行期内所可能遭遇的最大地震加速度累积概率(Pall)曲线和概率密度(Pa)分布曲线,分别如图3和图4所示.
考虑在由元件C1、C2构成的并联系统中,如何配置负载冗余元件R使系统可靠性更高,假设X1,X2,Y服从参数为λ1、λ2、λ的指数分布,比较以下两个系统的寿命:

图3 场地最大地震加速度累积概率曲线Fig.3 Accumulated probability occurrence of peak earthquake acceleration at the site

图4 场地最大地震加速度概率密度分布曲线Fig.4 Probability density distribution curves of peak acceleration at the site
如前所述,反应谱曲线的形状可以采用确定性的分布.但值得指出的是,统计的反应谱的形状,即加速度放大系数,一方面随结构阻尼比的大小发生变化,这种变化遵循一定的规律,可按公式进行计算;另一方面,这种变化又和地震波的特性相关,具有一定的随机特征,根据文献[1]的建议加速度放大系数(α)可按正态分布规律进行考虑,如图5所示.图中横坐标代表随机值与确定性数值平均值的比例R,括号内的数值则代表10%和90%概率时偏离中值的比例.

图5 输入加速度反应谱放大系数取值的分布密度函数Fig.5 Distribution density function of the amplification coefficients for input acceleration spectra
2 多向地震动输入条件下楼层谱的计算
2.1 楼层谱的计算方法
采用Monte Carlo方法进行核电厂楼层谱的概率分析时,对于单个模拟样本仍然采用确定性的计算方法.
楼层谱有时又称为结构内部反应谱,定义为结构内某一支承点上具有角频率为ωe和阻尼比为ζe的单质点体系的最大地震响应.较常采用的为加速度反应谱.核电厂设计中一般选用运行安全地震动(常取为极限安全地震动的1/2,或1/2SSE)作为设计基准.核电厂设计一般都具有比较高的安全性,在这种地震作用下,结构响应基本上处于弹性范围内.故楼层谱的计算一般采用弹性反应谱.如果在役核电厂建筑需要进行非线性动力响应分析[6],也不难在本文框架内实现,只需对公式略作调整便可.楼层谱的计算可采用时程法,即按输入地震波计算结构支承点的响应时程,再计算楼层谱.对于确定性方法来说,这样比较准确,计算工作量也不算大.但对于概率统计法来说,由于样本数量多,工作量就很大.所以,许多研究者提出直接从输入地震波的反应谱计算楼层谱的方法.早期提出这一方法的是Kapur等[7]和Biggs等[8],方法比较简单,但是近似程度高,所得结果相当保守,后来不少学者做了改进,提高了计算精度,但相对复杂,同时也有一定的局限性.本文主要研究地震动不确定性的影响,所以选用Kapur方法,但进行一定改进,使结果更为准确.
现将Kapur方法的基本内容简述如下.楼层谱的计算采用模态综合法,即对结构的各主要模态分别进行响应计算,然后加以综合.令结构第j模态的楼层加速度反应谱值为Sj,结构第j模态的角频率为ωj,地面输入加速度的最大值为ag,则多自由度体系结构计算点(支承点)的楼层谱值可分别计算如下:

式中:ΦSj为第j模态结构计算点的模态值;ηj为结构第j模态的参与系数;Sas为相应于结构频率ωj的地震动输入反应谱值;Sae为相应于振子频率ωe的地震动输入反应谱值.动力放大系数α1和α2按式(4)计算,当ωj/ωe=1时,αp按表2确定(Kapur给出),其他情况可根据曲线描绘插值获得.


表2 ωj/ωe=1时的动力放大系数(结构阻尼比5%)Tab.2 Dynamic amplification factorαpatωj/ωe=1(for structural damping ratio 5%)
式(1)~(4)针对结构的每一主要模态分别进行计算,然后按平方和开方的原则综合获得总响应.当结构的模态分布比较密集时,对密集模态先求得绝对值和,再和其他模态按平方和开方组合.对于ωe小于结构基本频率的情况,计算总响应时,先按式(3)方括号内的第一项进行各模态的平方和开方组合,再与第二项直接求和.求取结构计算点某一方向的楼层谱时,分别计算地震动三分量的贡献,然后按平方和开方组合.
动力放大系数α1、α2和αp实际上还和结构的振动模态形状(质量和刚度分布)以及计算点在结构中的位置有关,式(4)和表2给出的值是比较保守的.本文根据典型的核电厂房结构计算模型,通过不同地震波的统计分析得出峰值动力放大系数的合理数值.
2.2 考虑地震动不确定性楼层谱概率统计分析
为了研究核电厂有效使用年限内,地震发生的不确定性对核电厂结构和设备地震响应的影响,本文采用如下的实现方法.依据地震动参数的概率分布密度函数,通过随机数选取生成各参数的样本空间;再对结构进行确定性的抗震分析,将其作为基本过程,获得各组随机样本所对应的楼层反应谱的计算结果;然后对结果进行统计处理,得出概率意义上的楼层反应谱的计算值.按照ASCE4-98的规定,保证率达到90%以上的楼层谱可选为设计楼层谱.
在本文计算中考虑了两种地震动参数不确定性的影响.其一是场地最大地震加速度的随机性,其概率分布密度函数按50a运行期内的场地最大地震加速度概率密度分布曲线(Pa)来考虑,如图4所示.其二为反应谱加速度放大系数的随机性,其概率分布密度函数按ASCE规范建议的正态分布进行考虑,如图5所示.计算中,结构和地基均作为确定性系统进行考虑,在地震作用过程中参数保持不变.结构和地基的不确定性也是核电厂结构地震响应不确定性的重要来源,将另文进行讨论.
计算模型中参数的取值范围,可参照实际工程中试验数据的筛选方法,采用3d原则,其中d代表标准差,当随机值的大小符合正态分布规律时,在3d范围以外出现的概率仅为0.3%,对概率统计的结果影响较小.
3 算例与分析
选取一座一百万千瓦级压水堆核电厂反应堆厂房RX为背景研究地震动输入的不确定性对楼层谱结果的影响.厂房采用多质点悬臂梁模型,如图6所示,结构材料的确定性性能参数假设如下:材料,混凝土;动弹性模量,4×1010Pa;剪切模量,1.6×1010Pa;泊松比,0.2;质量密度,2500kg/m3;阻尼比,7%.地基的确定性性能参数假设为质量密度ρ=2600kg/m3,动剪切模量G=1.2×1010Pa,泊松比γ=0.30,剪切波速vs=2150m/s.(1/2SSE)按场地安评报告,50a运行期内地震动峰值加速度的超越概率统计如表3所示.万年超越概率10-4相对应的SSE水准的峰值加速度为1.76m/s2,采用1/2SSE水准,即0.88m/s2的水平向峰值地震加速度作为楼层谱的设计基准,相应的反应谱曲线为RG1.60谱,其形状如图7所示.
3.1 样本空间数量的选取
为了进行楼层谱统计意义上的分析与处理,选取大数量(N组)的随机样本空间是必要的.
分别按100组、200组、300组、400组及500组样本组合,针对图6所示算例,对比反应堆厂房某高位点的水平向楼层谱的统计计算值.比较结果显示,100组随机数列样本组合便可满足精度要求,即样本对应设计加速度值的实际分布满足图4的要求,反应谱加速度放大系数的随机性满足图5要求.为了避免在随机统计过程中引入其他数值不确定性因素的影响,后续结果将统一按300组随机样本空间进行参数输入计算与楼层谱结果统计分析.

图6 反应堆厂房(RX)集中质量计算模型Fig.6 Lumped mass model for the RX plant
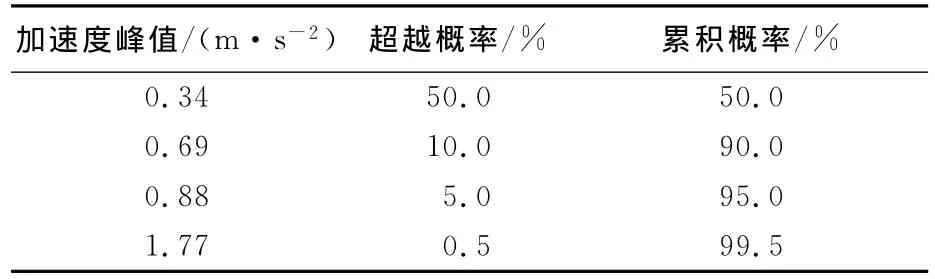
表3 厂址条件下50a运行期内地震动峰值加速度发生的概率统计Tab.3 Probability statistics of site-specific seismic peak acceleration during the operating period of 50years

图7 确定性数值分析水平向输入加速度反应谱Fig.7 Horizontal seismic input acceleration spectra for the deterministic numerical analysis
3.2 楼层谱数值结果比较与分析
根据设计单位的要求,作者计算了不同厂房结构,不同设备阻尼比的楼层谱曲线.因篇幅所限,本文只列出其中的典型工况.节点8的楼层谱(结构阻尼比5%,设备阻尼比2%)按确定性方法和概率统计方法计算结果的对比参见图8.确定性方法采用地震波时程进行计算,概率统计方法则采用Kapur方法进行计算.可以看出,采用保守的Kapur方法,90%保证率的概率统计方法计算的峰值的降低幅度达到10%左右.作者又根据反应堆厂房的计算模型,对Kapur方法的动力放大系数α1、α2和αp进行了修正,修正曲线如图9所示,经过计算检验,证明其与时程法的计算结果接近.据此,与确定性计算方法结果的对比如图10所示.此时,概率统计方法计算的峰值降低幅度达到30%.

图8 按Kapur方法计算的节点8楼层谱曲线(阻尼比2%)Fig.8 Floor response spectra at node 8calculated by Kapur method(damping ratio 2%)

图9 修正的动力放大系数Fig.9 Modified dynamic amplification factor

图10 按修正Kapur方法计算的节点8楼层谱曲线(阻尼比2%)Fig.10 Floor response spectra at node 8calculated by modified Kapur method
4 结 语
核电厂设计中,计算模型和计算参数的选择,以及地震动输入方面都含有较大的变异性.在楼层谱的计算中引入随机分析方法可以对设计的可信性以及结构和设备的安全性获得更为明确的概念.美国核电厂结构和设备规范建议,满足90%不超越概率的反应谱是适宜的选择,可满足核电厂设计的需要和安全要求[1、2].
本文结合我国地震危险性评价的客观实际,提出了一种考虑核电厂运行期内地震动发生不确定性对反应堆厂房楼层谱影响的有效分析方法.计算结果将为核电厂结构抗震安全性的评价以及安全管理提供重要参考.
[1]American Society of Civil Engineers Committee on Nuclear Structures.Seismic Analysis and Design,Chapter 5,Structural Analysis and Design of Nuclear Plant Facilities[S].New York:American Society of Civil Engineers,1980
[2]ASCE.ASCE 4-98 Seismic Analysis of Safety-Related Nuclear Structures[S].New York:American Society of Civil Engineers,2000
[3]中华人民共和国建设部.GB 50011—2001建筑抗震设计规范(2008年版)[S].北京:中国建筑工业出版社,2008
[4]中国国家地震局.GB 50267—1997核电厂抗震设计规范[S].北京:中国国家地震局,1997
[5]中华人民共和国建设部抗震办公室.建筑抗震设计规范GBJ 11—89统一培训教材[M].北京:地震出版社,1991
[6]CAMPBELL R D,HARDY G S,RAVINDRA M K,etal. Seismic re-evaluation of nuclear facilities worldwide overview and status [J]. Nuclear Engineering and Design,1998,182(1):17-34
[7]KAPUR K K,SHAO L C.Generation of seismic floor response spectra for equipment design [C]//Proceedings of ASCE Specially Conference on Structural Design of Nuclear Plant Facilities.Chicago:ASCE,1973:29-71
[8]BIGGS J M,ROESSET J M.Seismic analysis of equipment mounted on a massive structure [M]//HANSEN R J,ed.Seismic Design for Nuclear Power Plant.Cambridge:MIT Press,1970:319-343
