高速加工中心可靠性统计技术应用*

苟卫东

(青海一机数控机床有限责任公司，青海西宁 810018)

我国对数控机床的可靠性研究工作始于上世纪80年代末期，通过对部分数控机床产品进行可靠性摸底和考核，初步了解了我国数控机床产品的可靠性状况并于上世纪90年代初颁布了一些相应的标准。近些年来，虽然我国机床行业的许多企业与有关高校合作研究可靠性技术，国产机床的可靠性水平在稳步增长，但与发达国家同类产品相比差距仍然明显。据统计，我国中高档数控机床的平均无故障工作时间值(MTBF)大约在500 h左右，而国外高档数控机床的MTBF值一般在1 000 h以上。针对以上问题，国家科技重大专项中对2009年度承担的高速加工中心提出了整机MTBF达到900 h的可靠性考核指标。

1 影响可靠性的主要因素

首先，数控机床产品的可靠性是使用和现场运行过程中暴露出来的质量属性，考虑产品使用的时间因素和环境因素，未经使用的产品不能真实评价其可靠性水平，因此，数控机床的MTBF要真正反映产品在生产运行过程中故障间隔的真实情况;其次，要研究和分析作为工作母机的高档数控机床产品的可靠性特点，明确研发产品现场运行过程可能存在的各种故障隐患，既然数控机床是制造机器的机器，因而具有功能可靠性和参数可靠性的双重要求;最后，提高数控机床可靠性，就是减少或避免产品工作过程中所发生的各种故障。

因此要依据课题产品或类似产品的多发故障，在课题研究中探寻故障的主要隐患及其影响因素，包括自身设计缺陷，制造工艺和装配调试水平低下，早期故障没有在制造厂消除，而是直接带到用户中;外购元器件、关键功能部件和配套件，质量低劣，未经严格测试检验和筛选;系统软件缺陷，受外部干扰使变量被修改，程序丢失，参数错误等。软件缺陷导致故障成为影响系统可靠性的关键因素之一;以及人为附加的隐患，主机厂的管理人员或工程技术人员可靠性意识薄弱或可靠性素质缺乏，在产品研发和生产过程中，由人的主观因素埋下隐患;当然也可能由于售后服务指导不到位或用户使用和维护不当，造成人为隐患。上述表明，数控机床的可靠性涉及到生产厂的设计、制造、装配、供应和售后服务等厂内各部门，涉及到配套件、外协件的供应厂商，还涉及到机床用户，这是一项需要多个部门共同努力的系统工程。实施可靠性设计是实现产品可靠性提升的基础，但不是可靠性提升方法的全部。特别是数控机床生产过程中，在很多情况下，影响产品可靠性的突出问题，往往是制造过程、装配过程，配套件和外购件的选用以及早期故障没有消除等，占发生故障的比例很大。要强调可靠性试验方法，加强产品制造过程、装配过程、配套件和外购件的采购以及早期故障消除等过程的可靠性保证措施，实施系统工程，才能最终实现数控机床产品的可靠性提升。

2 产品性能可靠性建模方法

2.1 明确问题，规划数据收集方法和收集失效数据

数据收集方法:采用现场跟踪统计试验的方法，对机床发生故障和维修时间以及机床发生故障的模式和故障原因进行详细统计。

故障数据计数的原则:机床的每一个故障都按关联故障或非关联故障分类。若为关联故障，则每一个故障均按一次故障计数。非关联故障不应计数。如果机床有若干项功能丧失或性能指标超过了规定界限，而且不能证明它们是由于同一原因引起的，则每一项均判为机床的一个故障;若是由同一个原因引起的，则判为机床只产生了一个故障;如果机床有一项功能丧失或性能指标超过了规定界限，而且它是由两个或更多独立的故障原因引起，则以独立的故障原因数判为机床的故障数;如果机床在同一部位多次出现故障模式相同的间歇故障，则只判为机床产生了一个故障;到达寿命规定期限的配套件、耗损件的更换及超期使用的损坏不按故障计数;当机床出现致命故障时，若为关联故障，则立即按可靠性不合格判定。

2.2 可靠性数据的采集

2.2.1 数据的采集

根据《数控机床可靠性评定》，即标准 GB/T 23567.1－2009在进行可靠性验证、测定、评定时的故障判定原则、抽样原则、试验方法、数据处理、结果评定的总的要求，可靠性数据的采集原则为:(1)由于数控机床的质量缺陷，在规定条件下、规定时间内不能完成规定功能的事件便成为故障;(2)在用户正常使用之前的早期故障，由于是在规定的截取范围以外，所以不计为故障;(3)与整机功能暂时无关或影响较小的局部微小故障不计为故障;(4)不按规定操作使用而引起的误用故障不计为故障。

在进行数据采集之前，必须首先明确数控机床故障模式。笔者在参考《数控机床可靠性评定》的同时，根据加工中心的本身特点和使用中的实际情况，制定了加工中心故障模式表，见表1。

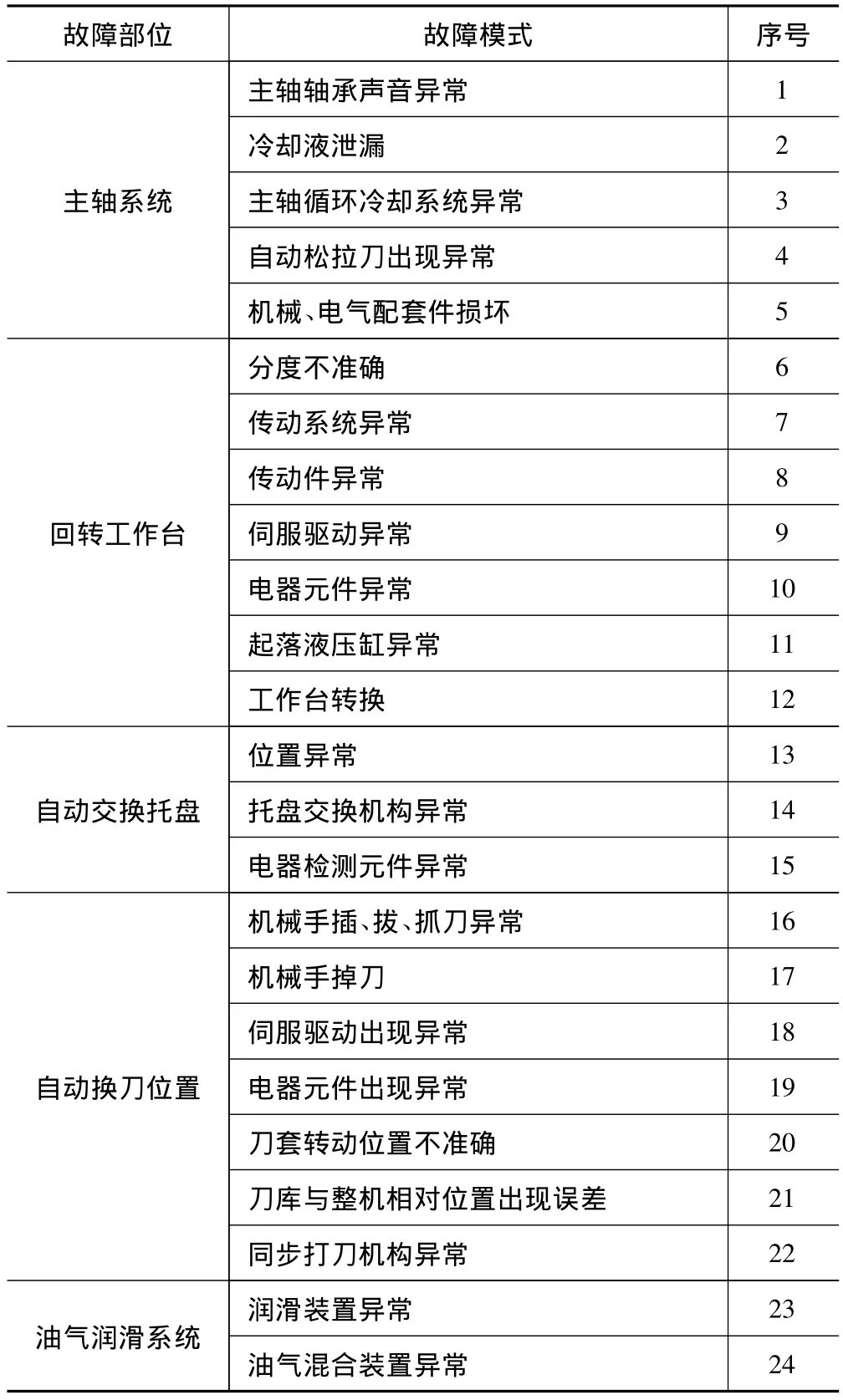
表1 加工中心故障模式表

要求:(1)从交付用户开始起，记录被试加工中心故障，在规定的时间间隔内对机床的运行情况记录;(2)按照故障发生时间顺序填写故障序号;(3)要求填表人签字，用户单位确认，以保证数据真实、可靠;(4)与协作厂家定好执行计划，由厂家派专人负责填写机床运行报告，一旦故障发生，立即根据故障判据和故障类型填写报告，恢复后应继续观察;(5)每隔一定时间进行中途检查，了解现场情况，并就具体问题进行指导。

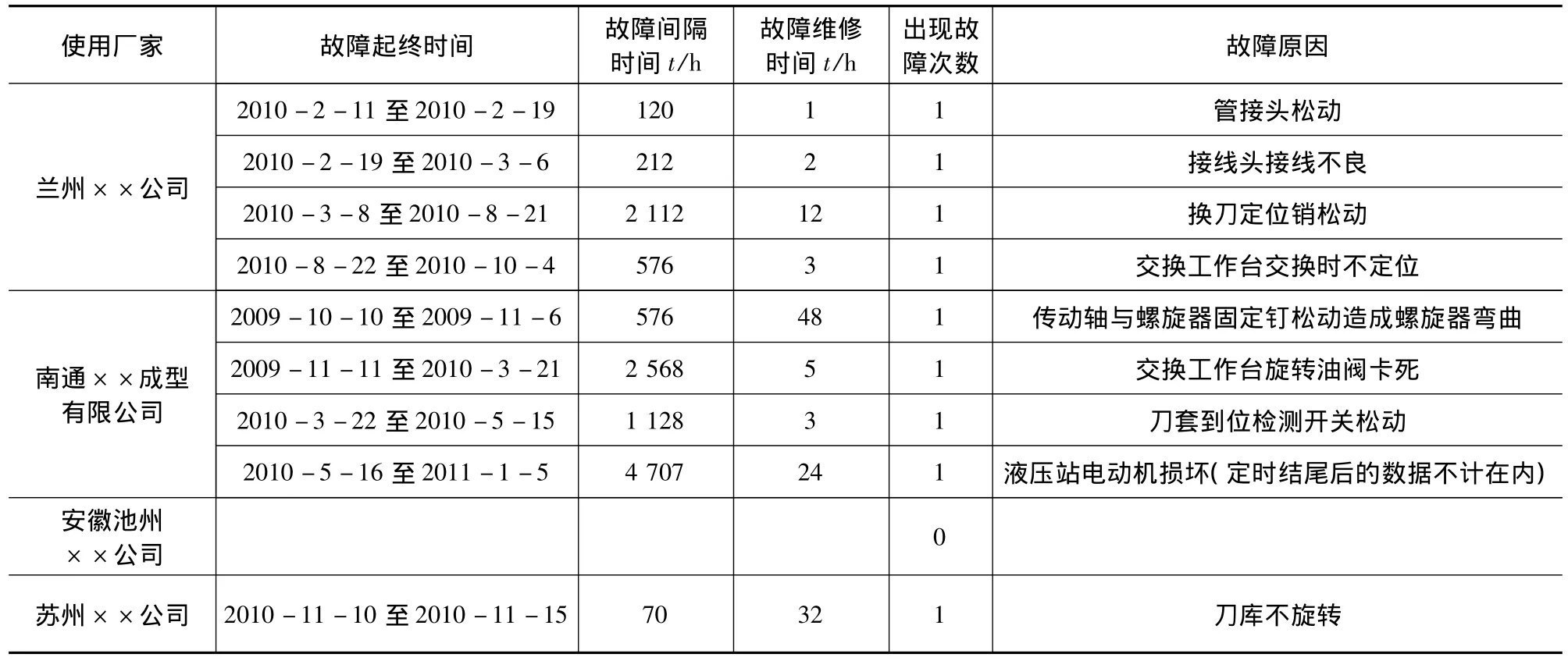
表2 故障信息统计表

2.2.2 数据的初步分析

计算每台加工中心所有故障间隔时间，将计算出的故障间隔时间按从小到大排列，并将故障间隔时间分组，并计算出每个区间故障间隔时间的频数和频率，做出频率表。

2.2.3 模型选择

调用MATLAB软件中Probplot命令，将采集到的故障间隔时间拟合成极值频率图、正态频率图、瑞利频率图、威布尔频率图，对比以上几个频率图形，初步确定故障间隔时间服从的分布模型。

2.2.4 模型参数估计

运用最小二乘法和一元线性回归方法计算分布模型的参数，即形状参数和尺寸参数估计。

2.2.5 模型检验

对模型进行k－s检验。它是将n个试验数据按从小到大次序排列，根据假设分布，计算每个数据对应的函数值F0(xi)并与经验分布值Fn(xi)比较，差值的最大绝对值作为检验统计量。

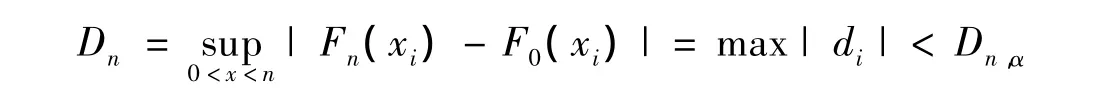
满足上式，接受假设。

2.3 产品性能可靠性评估方法

(1)参数确定与模型建立

对经过筛选的有效可靠性数据进行参数回归分析与假设检验，提出估计和给出可靠性分布形状参数、位置参数、尺度参数，进而建立可靠性评估模型，为可靠性评估、维修策略制定提供依据，对数控机床整机的可靠性预测提供理论支撑。

(2)评估方法

研究含有定时截尾寿命数据的寿命服从Weibull分布下小样本数据统计分析的可靠性评估方法。

3 可靠性统计计算

3.1 故障信息统计数据

在实际中，样本通常是一堆杂乱无章的数据，不经过一定的整理就难以提取有用的信息。整理数据的一种常用方法是将这些数据的所属区间适当地分成若干个小区间，相应地，这些数据也就分成了若干组，见表2。

根据整理的四台加工中心故障间隔时间数据，将数据分组如下:

(1)根据样本大小确定数据组个数，通常可以分为5～10组。取分组个数k=5。

(2)计算极差R。先从样本值中找出最小值m和最大值M，即:m=min(t1，t2，…，t8)和M=max(t1，t2，…，t8)，R=max(t1，t2，…，t8)－ min(t1，t2，…，t8)=2 568－70=2 498。

(3)确定组距。计算公式为d≈R/k=2 498/5≈500。

(4)确定各组端点值。计算公式为ak=a0+d×k(k=0，1，2，…，n)，其中，a0＜min{t}，an＞max{t}。一般取a0比数据的最小值小半个测量单位，即a0=69.5，a1=569.5，a2=1 069.5，a3=1 569.5，a4=2 069.5，a5=2 569.5等等。

(5)确定频数和频率。设第i个小区间(ti－1，ti)中样本值的频数为fi，则相应的频率为vi=fi/n(1≤i≤5)，即v1=f1/n=3/8=0.375，v2=0.25，v3=0.125，v4=0，v5=0.25。

根据以上计算内容做加工中心故障频率表，见表3。

用最小二乘法做威布尔分布函数参数估计:

设线性回归函数为

表3 加工中心故障频率表

3.2 可靠性统计计算模型建立

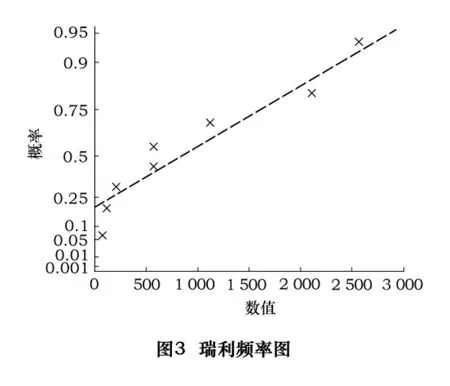
依据软件Matlab中probplot命令将故障间隔时间拟合成极值频率图、正态频率图、瑞利频率图、威布尔频率图，如图1～图4。

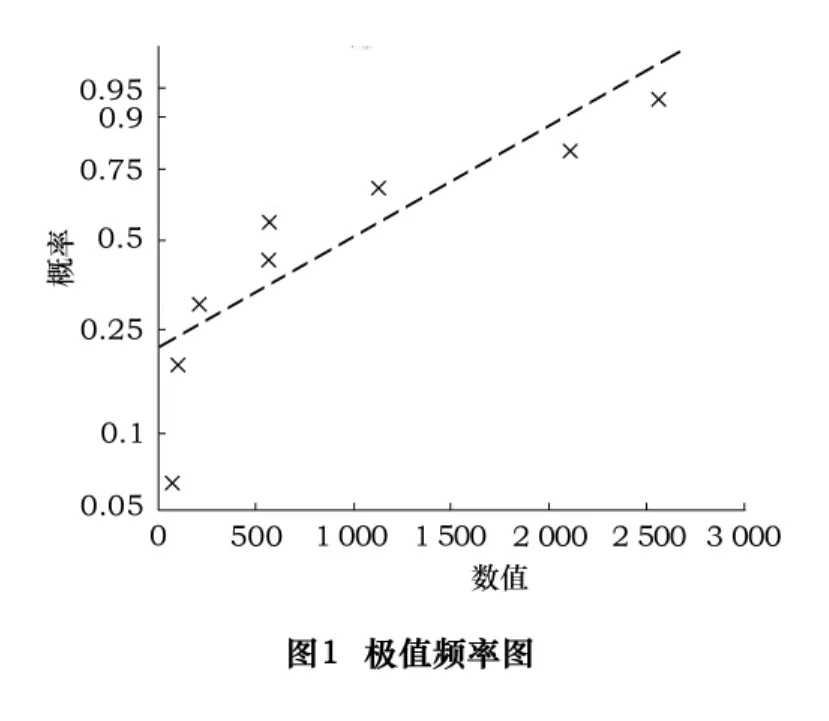
对图1～4比较可知，威布尔分布拟合的图比较好。所以8个故障间隔时间值可能服从威布尔分布。

3.2.1 威布尔分布参数估计

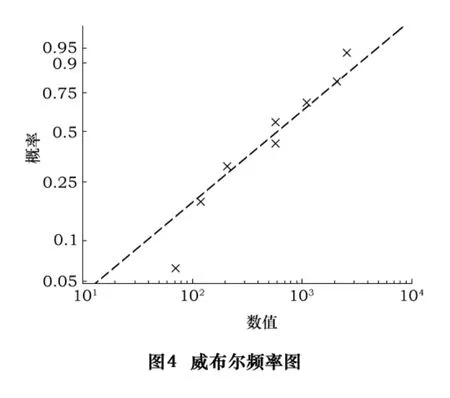
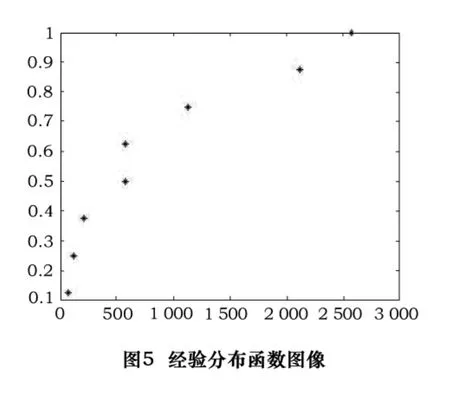
经验分布函数为

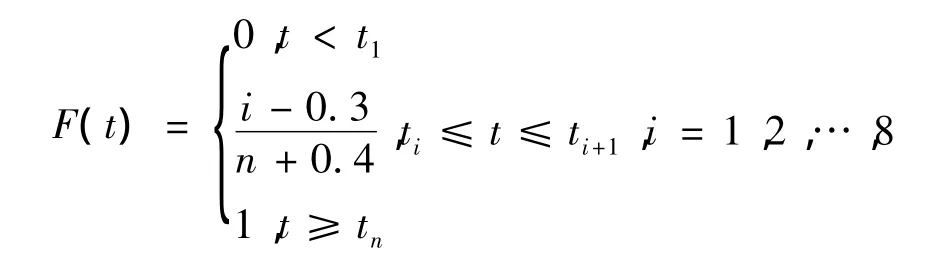
解 得对应的值:0.083 3，0.202 4，0.321 4，0.440 5，0.559 5，0.678 6，0.797 6，0.916 7，见图 5。

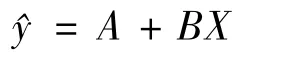
式中:y上方加^为了区别于实际观测值y;B为该直线的斜率;A为截距。当X=Xi时，实际观测值为试验的随机偏差，yi=^yi+ei=A+BXi+ei，则ei=yi－ (A+BXi)。为了使线性函数拟合得最好，需令偏差平方和最小。将Q(A，B)分别对A和B求偏导，令其等于0，解得

表4 x和y的值

由y=ln(ln(1/(1－F(ti))))，x=lnti确定 x和 y的值，见表4。

通过Matlab软件最小二乘法的拟合的程序:

即:A=－0.572 6，B=0.815 2。所以，一元线性回归方程:

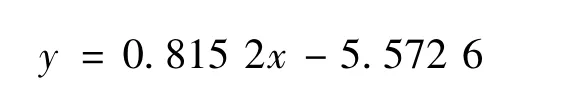
对于两参数威布尔分布，其累积分布函数为

式中:k≥0，k为形状参数;b＞0，b为尺寸参数。

对上式两端进行变换，并取自然对数得:

令:

由上式得k=0.815 2，b=930.636 3。所以:

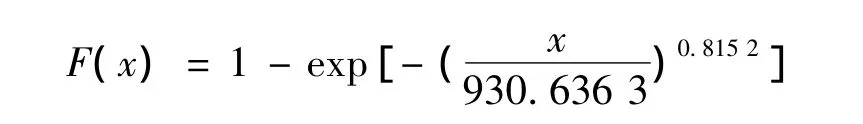
3.2.2 分布拟合的检验:采用d检验法

通过 Matlab，求出x=70、120、212、576、576、1 128、2 112、2 568 时，F(x)对应的值为 0.081 0、0.250 0、0.375 0、0.500 0、0.625 0、0.750 0、0.875 0、1.000 0。

经验分布函F8(x)对应的值0.083 3、0.202 4、0.321 4、0.440 5、0.559 5、0.678 6、0.797 6、0.916 7。

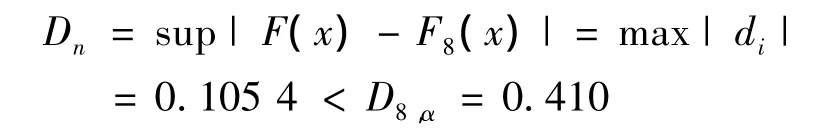
所以，故障间隔时间服从威布尔:

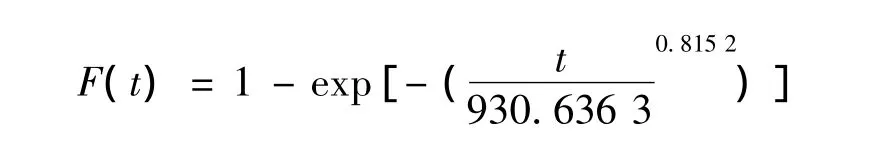
故障间隔时间概率密度函数:

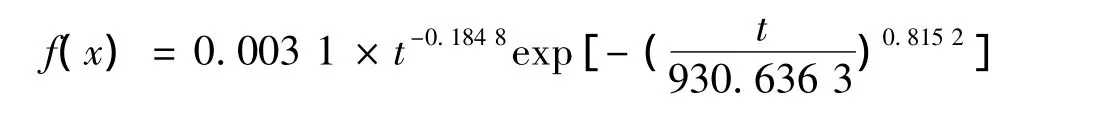
f(t)，F(t)的曲线分别如图6、7所示。

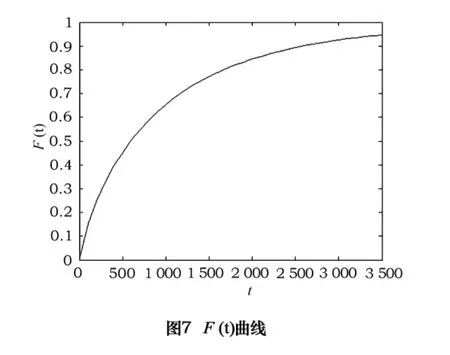
即r(t)=0.003 1 ×t－0.1848

失效率函数曲线图如图8所示。

3.2.3 线性相关性检验

依据Matlab命令R=corrcoef(x，y)计算x与y之间是否真正存在线性相关的关系。程序如下:

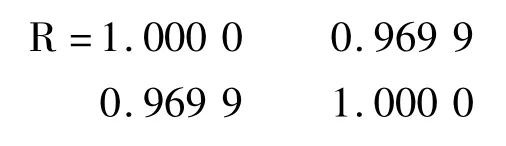
所以，相关系数是ρ=0.969 9。由标准表查得相关系数起码值ρα=0.549 4。即ρ＞ρα。说明x与y线性相关性。

3.3 加工中心可靠性统计计算

3.3.1 评定及MTBF的计算

经过上述分布类型的假设、参数估计、假设检验，已经确定了故障间隔时间的分布类型及参数，在此基础上进行可靠性特征量的评定及MTBF的计算。

加工中心故障间隔时间是指加工中心相邻两次故障间的时间。相应的可靠性指标有平均故障间隔时间，用MTBF表示，它是故障间隔时间T的数学期望E(t)。

加工中心的平均故障间隔时间只有故障间隔时间服从威布尔分布时加工中心的整个寿命周期内近似保持不变，实际上故障间隔时间本身是时间的函数。平均故障间隔(Mean Time Between Failure，MTBF)，也称为平均无故障时间，指可修复产品相邻两次故障间的平均时间。其数学表达式为

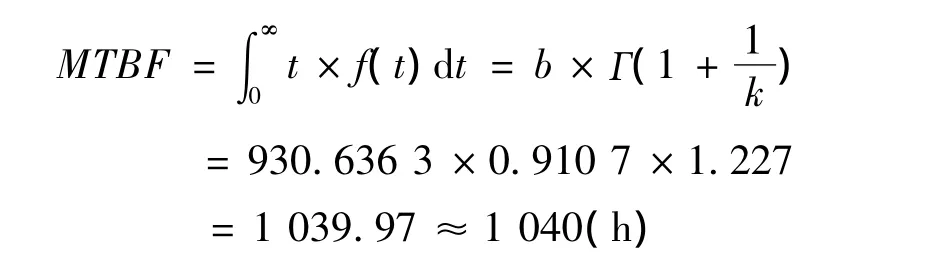
式中:f(t)为故障间隔时间的概率密度函数;k和b分别为威布尔分布形状参数和尺寸参数;Г为伽玛函数，其值可以查数学中伽玛函数标准表［1］。

3.3.2 MTBF 区间估计

(1)总体带估计参数

估计总体带估计参数，以某一给定的概率，落在多大的区间之内。

(2)估计的精确性(区间)和可靠性(概率)

设用θ*作为未知参数θ的估计值，误差不超过某一正数δ的概率P表示为

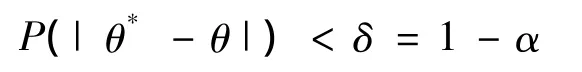
其中:α为显著水平;1－α为参数θ位于随机区间(θ*－δ，θ*－δ)的概率，称为置信概率，表示估计的可靠性;(θ*－δ，θ*－δ)为置信区间，表示估计的精确性。

(3)定时截尾寿命试验时平均寿命的区间估计

MTBF的区间估计是根据数据求得可靠性特征量MTBF的一个置信区间，这个区间以一定的概率(即置信水平)包括未知参数MTBF的真值。由于寿命试验数据的随机性，试验总时间T*可以看作是一个随机变量。

采用定时截尾的试验指标区间估计，置信水平1－α=90%，即α=10%，平均故间隔时间的双侧置信区间的区间估计满足公式:

式中:r为生故障次数;T*为定时截尾试验总试验时间。

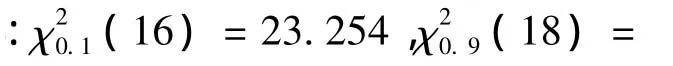
4 可靠性统计技术应用结论

本文通过对我公司高速加工中心用户使用过程故障信息跟踪并统计，先假设分布类型，然后进行线性相关性检验，拟合分布检验，最后确定高速加工中心的故障时间服从威布尔分布。并计算中得出MTBF等于1 024 h;根据国家机床质量监督检验中心对该类机床在现场进行可靠性加载试验，可靠性试验报告编号2011KB18，得出可靠性指标MTBF等于928.4 h。由于试验过程中是按最大负荷的75%连续加载，而实际生产中有间歇性的装卸工件时间或非连续运行时间，并且机床不是极限条件下运行，因此统计方法得到的可靠性指标与试验状态下得出的可靠性指标有所差异，但与本文所介绍的可靠性统计方法得出的结论基本一致。

［1］王超.机械可靠性工程［M］.北京:冶金工业出版社，1992.