nToeplitz数字图像反降晰方法①

石瑞英， 王玉霞， 李 帅

(1.佳木斯大学信息电子技术学院，黑龙江 佳木斯 154007;2.七台河科技与信息产业局，黑龙江 七台河 154600)

0 引言

获知对象的真实面貌是科学观测的目的之一.由于物理原理或技术条件的限制以及噪声的介入，我们常常只能获得一个不清晰的图像.因此，怎样将图像复原就成了一个具有普遍性的问题，对工程、医疗保健、航空航天、军事、安全保卫等各个领域都具有重大的实际意义.

1 Toeplitz方法图像反降晰原理

图像复原的一类基本问题是反降晰，即依据一个降晰并受噪声沾染的观测来估计原来的图像x(u，t).如果成像系统的降晰函数h(u，v)已知，则反降晰问题是一个常规的反卷积问题;否则它是一个盲目反卷积问题.

Toeplitz方法的基本思想是将图像信息与降晰函数的卷积运算转换为图像序列与Toeplitz核函数的矩阵运算，这样可以将反卷积问题转换为矩阵运算求逆的问题.下面简单介绍Toeplitz方法的基本原理.

1.1 Toeplitz方法一维反降晰原理

假设一维降晰核为h=(h1，h2，h3)，降晰对象为一维数组x=(x1x2x3x4x5)，则两者卷积结果如图1.

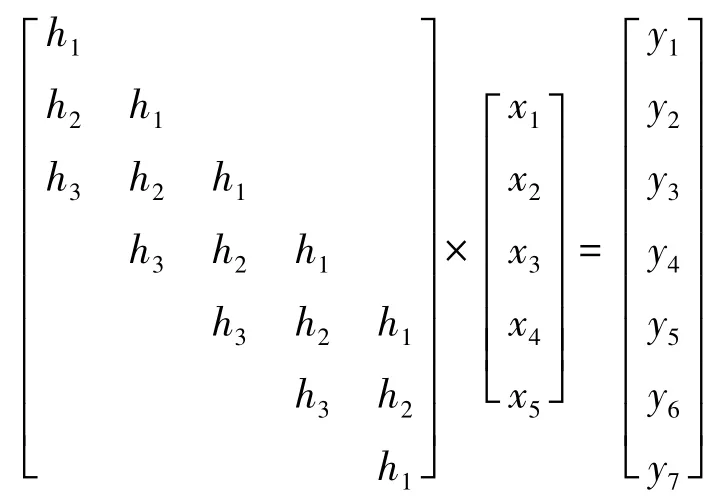
图1

其中:

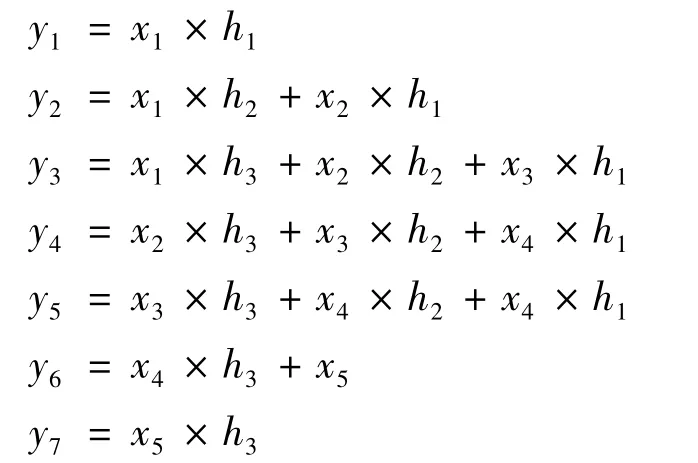
从卷积结果可以发现，x被降晰后不仅相应的元素值发生了改变，而且尺寸也变大了.反降晰过程需要对降晰核矩阵求逆，可是从图1可以发现，降晰核矩阵的行n大于列m，不是一个方阵，无法求逆.这就需要对降晰核矩阵进行处理，然后求逆，得到逆阵，再用x降晰后得到的y数组与逆阵相乘，得到数组X，X=(0，x1x2x3x4x50)，即数组X就是对数组y反降晰最终得到的结果.

1.2 Toeplitz方法二维反降晰原理

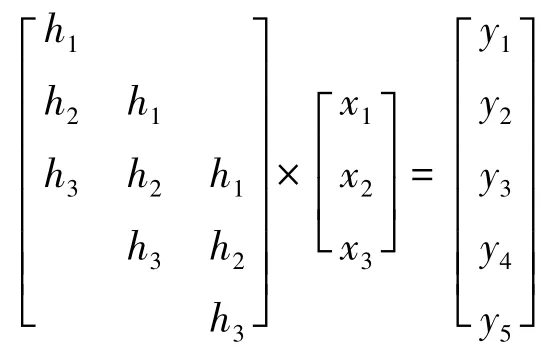
图2

其中:

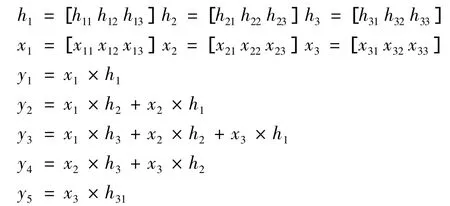
反降晰过程需要对降晰核h矩阵求逆从卷积结果可以看出，卷积后不仅单元x值发生了变化，而且行数也增加了两行.我们以降晰核h1单元矩阵为例求逆，由于降晰核h1单元矩阵的行大于列，不是一个方阵，无法求逆.这就需要对降晰核h1单元矩阵进行处理、扩充、得到如下单元矩阵如图3:

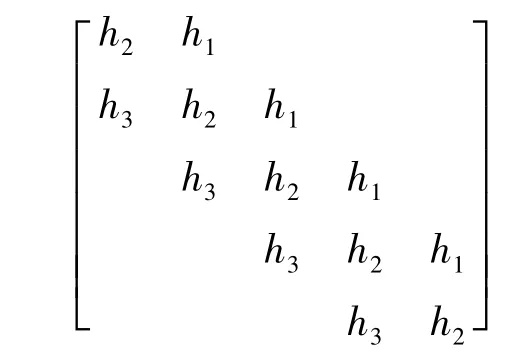
图3

将各单元矩阵带入到图3矩阵中，得到最终的Toeplitz矩阵TH，结果如下图4所示:

将TH矩阵求逆得到逆矩阵G.反降晰过程需要图像y变为一维数组，因此将y数组从第二行开始，每行中的元素都平移到上一行元素的末尾来形成一维数组，再将得到的数组转置得到列排列的数组.

图4

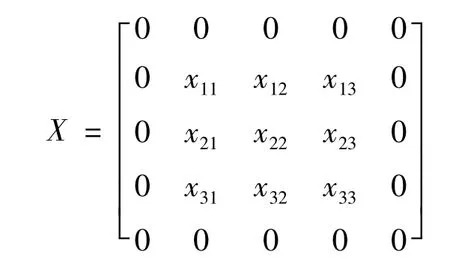
图5

2 反降晰的模拟实现

首先建立单元矩阵数组，再建立单元矩阵流程图，然后建立主矩阵数组、主矩阵流程图，如下图6所示:

将单元矩阵中的元素释放到主矩阵中，最终建立出来的Toeplitz矩阵，如下图7

3.1 降晰核函数的选取

3.2 降晰图像和反降晰结果的对比

选择图8(a)所示作为降晰对象，利用式(1)所示的降晰核函数作为降晰核，得到的降晰图像如图8(b)所示，最终得到的反降晰图像如图8(d)所示.

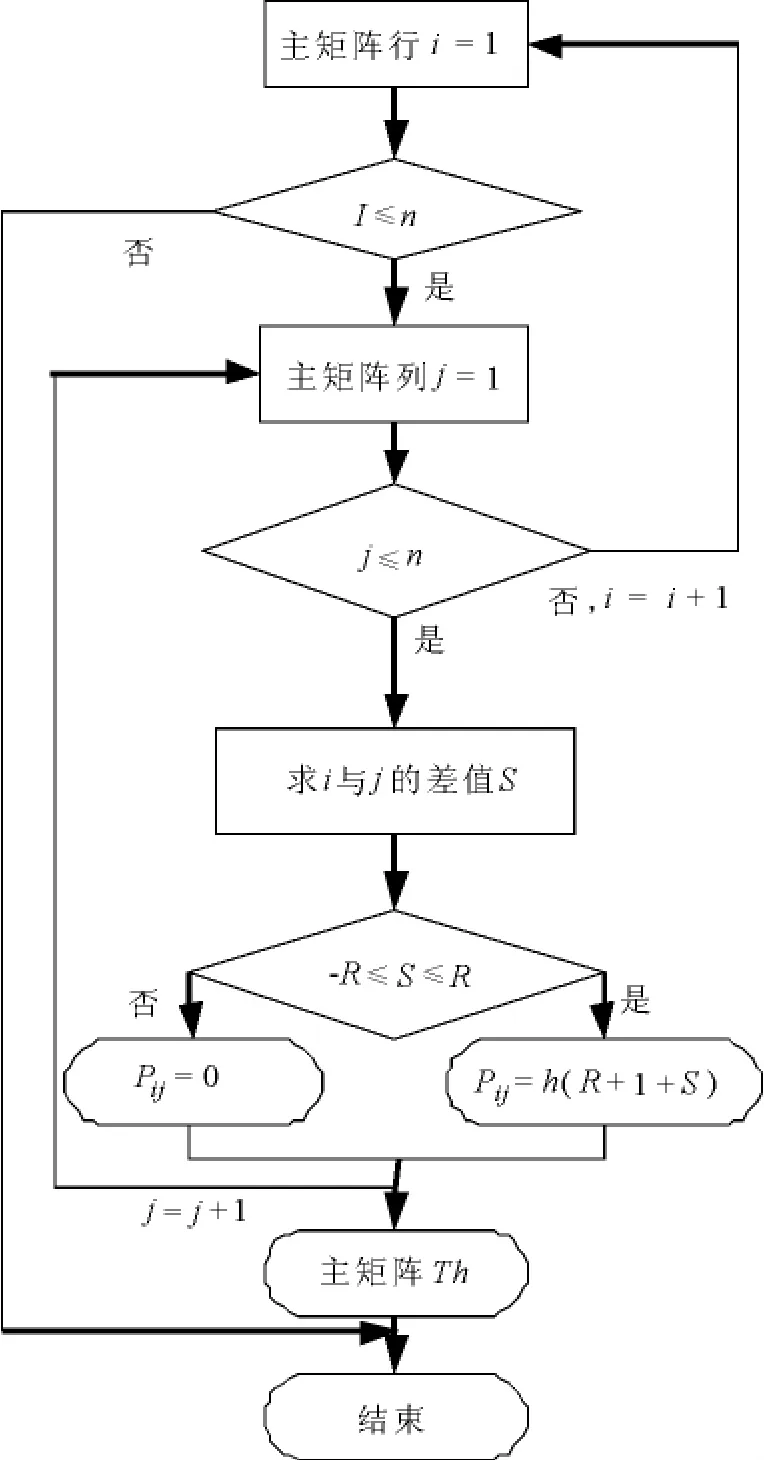
图6

从图8中可看出原始图(a)通过降晰后变成不清晰的图(b)，将图(b)在进行反降晰后又变的清晰图(d)，在图(c)和图(d)中就可明显的看出降晰和反降晰的区别，在图(e)和(f)中我们看出原始图和反降晰图非常的接近.即用反降晰法恢复了图的本来面目.

图7

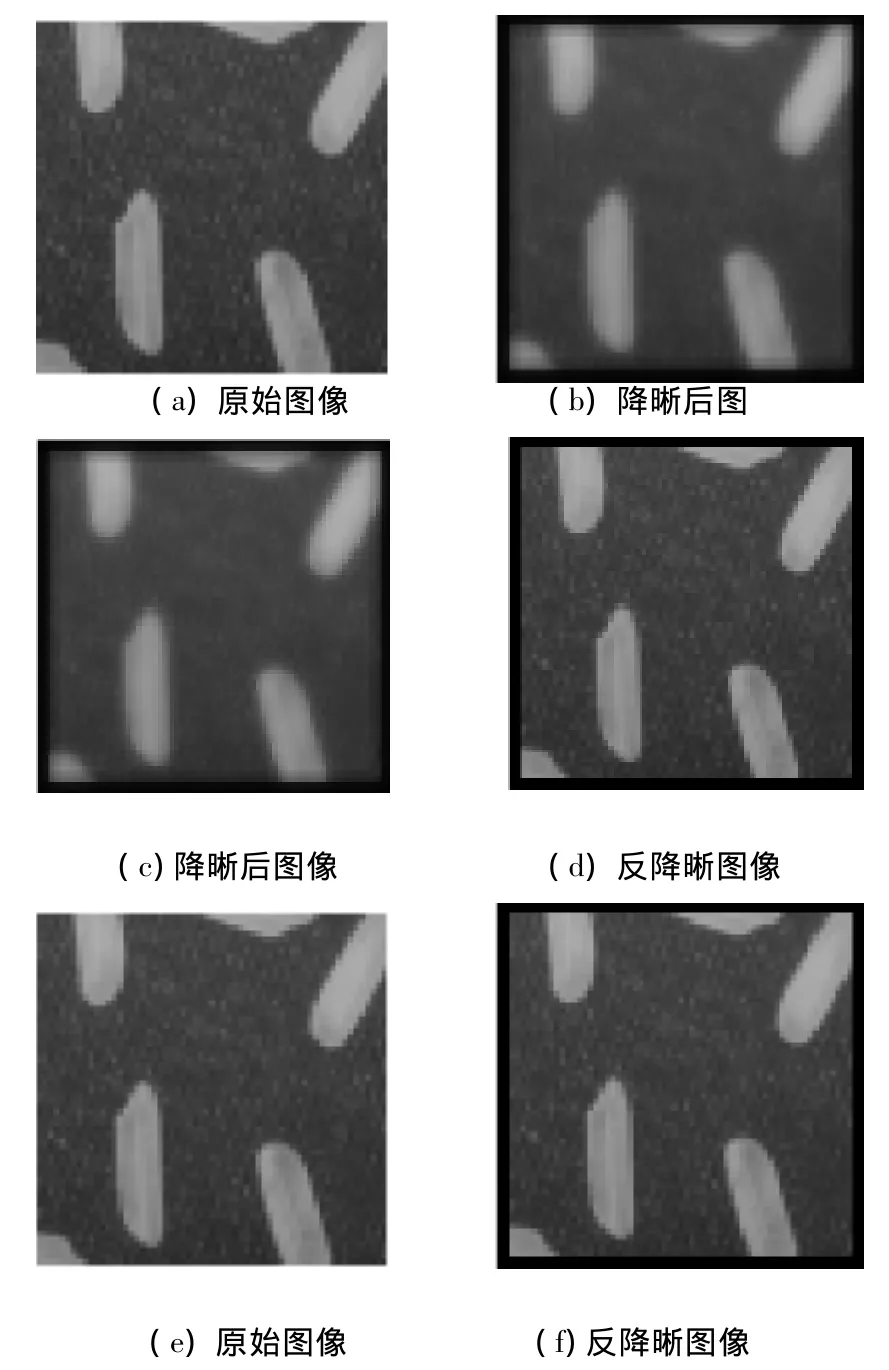
图8 原始图像和反降晰图像对比

4 结束语

通过仿真实例的对比，可以确认Toeplitz方法确实是有效地一种反降晰方法.它将矩阵间的卷积运算转化成了代数运算，使得反卷积方法可以在matlab软件中实现，极大拓展了可应用性，为这种技术的应用和发展打开了广阔的空间.当然Toeplitz方法存在计算量大的缺点，使只能对小尺寸图片进行处理.怎样进一步优化算法，减少计算量就成了下一步的研究方向.

[1]Rafael C.Gonzalez.Richard E.Woods.Steven L.Eddins.数字图像处理[M].北京:电子工业出版社.2007.

[2]邹谋炎.反卷积和信号复原[M].北京:国防工业出版社.2001.

[3]张远鹏.董海周文灵.计算机图像处理技术基础[M].北京:北京大学出版社.1996.9.

[4]罗军辉，冯平.MATLAB7.0在图像处理中的应用[M].北京:机械工业出版社.2007.

[5]张坤.陈凯.一种在光照变化条件下的人脸图像预处理算法[J].福建电脑.2010.9:6.