基于Copula函数和王变换的巨灾死亡率债券定价研究
2012-09-27尚勤,秦学志,张悦玫,胡友群
尚 勤, 秦 学 志, 张 悦 玫, 胡 友 群
(大连理工大学 管理与经济学部,辽宁 大连 116024)
0 引 言
巨灾死亡率债券是国际上新兴的一种风险证券化产品.这类特殊的债券交易可以提升寿险公司承保和抗风险能力,增强保险业在救灾、抢险以及灾后重建中的作用,减缓国家的财政压力.同时,还可以为资本市场的投资者提供新的投资工具,有利于实现保险业与资本市场的融合与共赢.2003年底瑞士再保险公司发行了世界上第一只死亡率债券,成为死亡率风险证券化具有开创意义的尝试.随着世界范围内巨灾事件的增多,此类产品的研发已得到国际理论和实业界的强烈关注.但中国在此领域的研究还处于定性讨论阶段.目前,我国巨灾风险不断升级,保险业发展滞后,此类产品定量研究的必要性和紧迫性不断凸显.
巨灾死亡率债券定价有两个关键点或难点:一个是对合同中指定地区的人口死亡率风险的合理预测;另一个是定价的方法要适用于此类债券交易所处的不完全市场.有关人口死亡率的预测,最初采用的是静态模型,并未考虑时间因素的影响,不能反映死亡率随时间的动态变化.Lee等[1]考虑到死亡率变动与年龄、时间的相关性,提出了Lee-Carter模型,给死亡率预测研究带来了突破性进展.随后,一些学者对Lee-Carter模型进行了扩展和修正[2、3].近年来,一些学者利用随机过程理论更加细致地刻画出了死亡率的波动特征.如Milevsky等[4]通过It 死力过程来刻画死亡率的随机变动;Dahl[5]应用正随机利率模型刻画死亡率等.死亡率预测研究已经取得较为丰硕的成果,但应用于巨灾死亡率债券触发指数的设计还存在一些不足.现有研究侧重于单个地区死亡率的预测,而巨灾死亡率债券要预测的是多个地区的联合死亡率状况.巨灾发生时,有些地区的死亡率可能会出现跳跃,并且不同地区死亡率之间不可避免地会具有一定的相关性.现有研究均缺乏对这些特征的有效描述,难免会造成对死亡率风险的低估,影响巨灾死亡率债券定价的准确性.另外,关于死亡率风险证券化产品具体定价方法的研究,已有学者进行了尝试.Friedberg等[6]应用资本资产定价模型(CAPM)和以消费为基础的资本资产定价模型(CCAPM)计算死亡率风险的费用,研究得出利用以上基于完全市场假设的定价理论度量死亡率风险会出现较大的误差.Dahl等[7]将风险中性定价方法应用于死亡率风险证券化产品定价,在理论上得出了较好的结果,但还未能进行实证研究.Wang提出一类均衡定价方法[8、9],利用概率分布扭曲的方法实现了在不完全市场中的风险定价,并且具有简明的表达式,在实证研究中具有较明显的优势.Lin等[10]将Wang变换方法引入巨灾死亡率风险定价研究,并进行了相关数据分析,验证了Wang变换方法在巨灾死亡率债券定价研究中的可行性和有效性.本文利用跳-扩散过程刻画死亡率的随机波动及其跳跃特征,引入Copula函数对不同地区死亡率之间的相关性进行描述,以增强多个地区联合死亡率预测的合理性;并在新的理论框架下运用王变换,进一步完善巨灾死亡率债券的定价模型.
1 死亡率指数构建
为了更加合理地构造死亡率指数,本文从加强死亡率的跳跃性和相关性这两个重要特征的刻画,对现有研究进行完善.
1.1 死亡率服从的跳-扩散过程
首先,利用含Poisson频率的跳-扩散过程描述某个地区人口死亡率的随机变化特征.此随机过程能够描述出巨灾发生时死亡率出现跳跃的特征,相对于不带跳的随机过程,更加符合死亡率随机波动的实际情况.
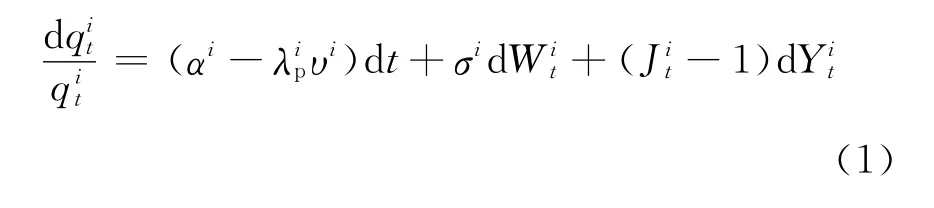
式中:αi为地区i死亡率指数瞬间变化的期望;σi为死亡率指数的瞬间方差为标准布朗运动;为参数为的泊松过程为跳跃频率为跳跃幅度,服从对数正态分布期望值为υi+1,即

死亡率指数在(t,t+Δt)内发生跳跃的概率为
需要说明的是含有跳跃项的随机过程还有很多,本文综合考虑随机过程的代表性和运算性质选用了以上含Poisson频率的跳-扩散过程.当然,根据实际需要利用其他带跳的随机过程对死亡率进行刻画时,本文的定价方法同样适用.
1.2 基于Gumbel Copula函数的死亡率指数
由于地理或人文环境的相似性,不同地区的死亡率并不是相互独立的,而是具有一定的相关性.缺乏死亡率之间相关性的刻画是现有死亡率指数构建存在的主要不足.事实上,巨灾爆发时相邻灾区的死亡率协同变化明显增强,甚至可能同时出现跳跃的极端情形.为了进一步完善死亡率相关性特征的刻画,本文引入Copula函数.
Copula函数是探索随机变量之间非线性相依结构的有力工具.不同类型的Copula函数可以描述不同的相关性模式[11].本文主要讨论Archimedean Copula函数族.这类Copula函数处理尖峰厚尾特征的观测样本(人口死亡率普遍具有尖峰厚尾的分布特征)具有良好的性质,其函数的具体表达式为

其中φ(·)称为Archimedean Copula函数的生成元.按照生成元的不同,Archimedean Copula函数分为二十几种.其中最具代表性的有3种,如表1所示.

表1 具代表性的Archimedean Copula函数Tab.1 Representative Archimedean Copula functions
图1是3种Archimedean Copula函数分布密度图.Clayton Copula函数分布密度上尾低,下尾高,对分布的下尾变化十分敏感,能快速捕捉到下尾相关的变化,可用于描述下尾相关性特征;Gumbel Copula函数密度分布上尾高,下尾低,对分布的上尾变化十分敏感,能快速捕捉到上尾相关的变化,可用于描述上尾相关性特征;而FrankCopula的分布密度具有对称性,对上尾和下尾相关性描述都不敏感,难以捕捉到尾部相关性变化.

图1 3种Copula函数分布密度Fig.1 Three kinds of Copula function distribution density
不同地区死亡率之间的相关性,主要表现在上尾相关性特征.即巨灾发生时一个地区死亡率上升,其他地区死亡率上升的概率增大的情形.例如印度洋海啸事件,导致十多个国家的人口死亡率的协同上升.因此要利用能够快速捕捉这种相关性特征的Gumbel Copula函数来刻画不同地区死亡率的相关特征,以此完善死亡率指数的构造.
现将二元Gumbel Copula函数扩展到n元:

则由n个地区人口死亡率生成的n维随机向量的联合概率分布可写成

其中

2 双因子王变换下的巨灾死亡率债券定价模型
巨灾死亡率债券定价的基本原理与其他类型债券相似,都是计算债券预期未来现金流的现值.由经典的资产定价理论可知,在一个完全市场中,任何一种现金流均可由该市场中交易的某些证券组合加以复制[12].而巨灾死亡率债券的现金流受地震、飓风、洪水等自然灾害或其他保险风险的影响,通常无法由股票、债券等传统资产的组合来复制,只能在不完全市场的条件下对死亡率关联债券进行定价.为克服不完全市场定价这一难点,本文利用王变换方法.
2.1 王变换
王变换定义扭曲算子(distortion operator):
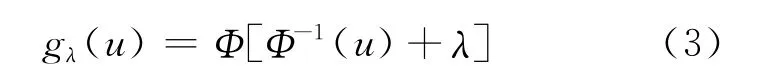
其中Φ(·)是正态分布函数,λ为参数,0<u<1.
设随机变量Z为保险市场中在区间[0,T]的负债,记F(z)为其分布函数,则扭曲分布

即为F(z)的单因子王变换(one-factor Wang transform).
这里,λ为市场风险价值,反映了保险市场中的系统风险或公司特有的不可对冲的风险水平.单因子王变换要求概率分布已知.然而,实际研究中概率分布经常是根据有限的样本数据估计得到的,即使选择很好的样本和参数估计方法也不可避免地会出现参数估计结果不准确的情况.为了解决这一问题,Wang给出了双因子王变换(two-factor Wang transform):

其中Q是t分布函数.
王变换的意义在于产生了一条经过“风险调整”后的“价格曲线”F*(z).用F*(z)替代原累积函数F(z)求期望,再通过折现计算,就可以得到不完全市场中负债的公平价格.
2.2 巨灾死亡率债券的定价模型
本文利用Gumbel Copula函数构造的死亡率指数,只能通过参数估计得到其分布情况.为了减少由于参数不确定性带来的误差,下面通过双因子王变换为巨灾死亡率债券定价.
设单位本金在t时刻的损失为
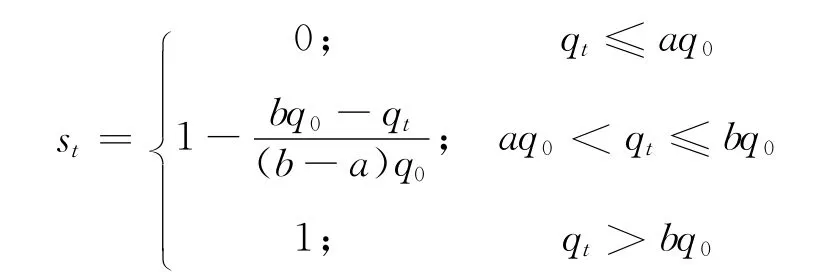
其中1<a<2,1<b<2且a<b.
则到期日债券的价值

设r为无风险利率,则面值为F的巨灾死亡率债券的价值
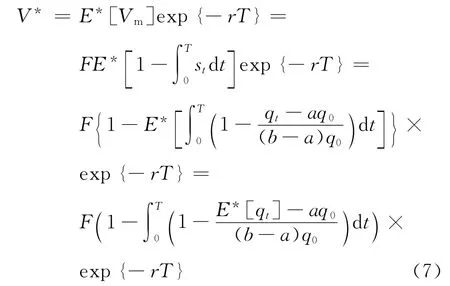
其中死亡率指数联合分布为
1) 从通航净高尺度看,与桥梁净高相关。根据《运河通航标准》[10]规定,长三角地区二~四航道等级的水上过河建筑物通航净高尺度为7 m,对标大运河全线7 m以上净高桥梁,目前共计342座,占比85.3%(见表7),相比2006年发布《办法》前增长13个百分点,但仍有50座非标桥梁存在,主要分布在浙江内河四级航道,但按照浙江段三级航道整治工程计划,桥梁改建后净高均为7 m。对于其余河段非标桥梁,或因沉降略微下降高度或可通过其他航道绕行,因此运河全线通航净高以7 m为限。
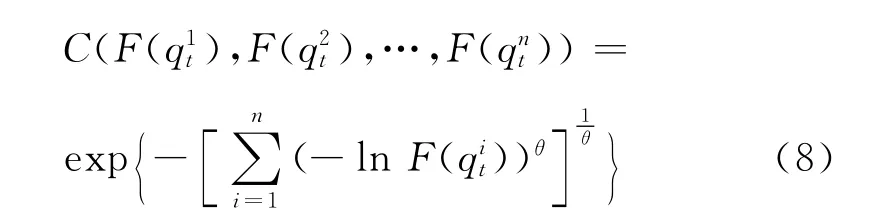
E*为联合概率分布C双因子王变换为C*后的期望值,

3 实证分析
本文利用汶川地震受灾最为严重的两个省份——四川省和甘肃省的人口死亡率数据进行相关的实证分析.
3.1 数据说明
人口数据来自中国人口信息网、《中国统计年鉴》和《新中国五十年统计资料汇编》.无风险利率初值的选取为2007-12-29发布的1年期Shibor 5日均值4.569 7%,相关数据来自http://www.shibor.orgshibor/web/shiborDefDownIFrame.jsp.
由图2可以看出,自建国以来两省的人口死亡率均呈现下降趋势,且具有相类似的波动形态.在1959~1962年3年自然灾害时期,两省同时出现死亡率的跳跃.

图2 四川省和甘肃省人口的死亡率Fig.2 Total population death rate of Sichuan and Gansu provinces
表2描述的是两组样本数据的统计特征,偏度均大于0,峰度均大于3.可以判断两组数据的分布均具有尖峰、厚尾和右偏的特征.进一步检验两个省人口死亡率的相关性,利用SPSS软件计算得出,Kendall相关系数τb为0.614,说明两组数据具有较强相关性.

表2 统计特征描述Tab.2 Statistical characterization description
3.2 参数估计
巨灾死亡率债券定价模型复杂且存在死亡率数据不足的问题,为减少参数估计的误差,本文整合现有参数估计方法的优势,分阶段估计参数.首先,采用Lee等[13]的跳辨识方法估计式(1)中的跳跃项参数.把跳跃项参数估计结果代入式(1)再利用 MCMC算法[14],估计剩余的参数αi和σi.进一步,利用Lin等[10]的方法估计市场风险价值λ,通过Kendall相关系数估计参数θ[15].结果如表3所示.

表3 巨灾死亡率债券定价模型中的参数估计结果Tab.3 Results of parameter estimation for pricing model of catastrophe mortality bonds
3.3 定价实例
设计票面价值10亿元人民币的5年期本金有风险的巨灾死亡率债券.该债券2007年底发行,2013-01-01到期.债券给付与四川省和甘肃省的联合人口死亡率指数qt相关联.
四川省和甘肃省人口总数比近似为7∶3(中国人口信息网),设四川省人口死亡率在死亡率指数中的权重为70%,甘肃省人口死亡率的权重为30%.用表示2007年四川省人口死亡率乘以表示甘肃省人口死亡率乘以1 000.由2008年《中国统计年鉴》可知6.65.则2007年实际死亡率指数为如果死亡率指数累积恶化程度超过2007年实际死亡率指数的10%,寿险公司就可以按比例减少对投资者的本金支付,作为死亡率风险补偿.如果累积死亡率超过2007年死亡率指数的30%,就可以提取全部本金支付.单位本金损失的表达式为

利用Gumbel Copula函数描述两省死亡率的相关性特征,进一步通过双因子王变换得出巨灾死亡率债券的定价公式:

式中:E*是qt服从概率分布为C*的期望值,其 中
由于V*没有显式表达式,下面通过Monte Carlo模拟计算债券价格,步骤如下.
第1步 生成n个服从(0,1)独立均匀分布的随机向量(v1v2)T.
第2步 生成(u1u2)T:令u1=v1;u2是如下方程的解:

这里,由于u2没有封闭解,采用牛顿迭代法求解.
t=1 时可得从而得到q1=
t=2 时可得从而得到q2=
t=5 时可得从而得到q5=
第4步 重复第1~3步k次,就可以用算术平均来估计qt.
第5步 代入价值公式(7)计算V.
利用Matlab软件编程计算,当模拟次数达到10 000次时结果趋于稳定,可得债券的价值为6.570 8×108.由于价格计算采用固定利率折现,计算结果的可靠度主要取决于通过Monte Carlo模拟得到的死亡率指数.利用K-S检验对死亡率指数的拟合优度进行检验.在0.95的置信水平下,P值为0.726 3,远大于0.05,通过检验.说明Monte Carlo模拟10 000次预测的死亡率指数与真实值拟合优度良好,进而验证了计算结果的有效性和一致性.
3.4 参数敏感度分析
下面分析定价模型中主要参数的敏感度.图3(a)是参数a和b单个变动或同时变动对巨灾死亡率债券价格的影响,可以为债券设计中a和b的取值提供一定的参考.图3(b)分析的是死亡率的跳跃参数的敏感度,可以看出死亡率跳跃参数对债券价格的影响是显著的,从而也验证了本文对死亡率跳跃特征的描述是必要的.

图3 参数变动下V*的趋势图Fig.3 Tendency graph of V* under the change of parameters
4 结 语
本文从我国巨灾严重、保险业发展滞后的客观实际出发,设计了一类巨灾死亡率债券,意在大幅度提高保险公司对巨灾保险的承保能力,扭转长期依赖国家财政的被动局面.在债券的设计和定价上,主要从死亡率指数的构造和不完全市场定价方法两个方面弥补了国际上现有研究存在的不足.利用含Poisson频率的跳-扩散过程和Copula函数构造的死亡率指数,涵盖了死亡率的跳跃性和相关性特征的描述,较已有研究对未来死亡率风险的预测更为合理.在定价方法上,通过王变换实现了在不完全市场中给巨灾死亡率债券定价的方法,避免了基于完全市场假设的定价方法可能产生的偏差.在理论推进的基础上,本文针对我国灾害多发区四川省和甘肃省两省的人口死亡率数据,给出巨灾死亡率债券的定价实例,并通过价格计算、参数敏感度分析等实证分析验证了定价模型的可行性和有效性.巨灾死亡率债券不仅可以实现死亡率风险的有效管理,还能为资本市场带来巨大商机,在我国拥有无限的潜力和发展空间.随着我国资本市场的成熟,不久的将来,巨灾风险证券化可能会成为巨大灾害的风险管理机制中的重要环节.
[1]LEE R D,CARTER L R.Modeling and forecasting US mortality[J].Journal of the American Statistical Association,1992,87(419):659-671
[2]BROUHNS N,DENUIT M,VERMUNT J K.A Poisson log-bilinear approach to the construction of projected life tables[J].Insurance:Mathematics and Economics,2002,31(3):373-393
[3]RENSHAW A E, HABERMAN S.Lee-Carter mortality forecasting with age specific enhancement[J].Insurance:Mathematics and Economics,2003,32(2):379-401
[4]MILEVSKY M A,PROMISLOW S D.Mortalityderivatives and the option to annualize [J].Insurance:Mathematics and Economics,2001,29(3):299-318
[5]DAHL M.Stochastic mortality in life insurance:market reserves and mortality-linked insurance contracts[J].Insurance:Mathematics and Economics,2004,35(1):113-136
[6]FRIEDBERG L, WEBB A.Life is cheap:using mortality bonds to hedge aggregate mortality risk[R]//NBER Working Paper 11984.Cambridge:National Bureau of Economic Research,Inc.,2005:13-28
[7]DAHL M,M /LLER T.Valuation and hedging of life insurance liabilities with systematic mortality risk[J].Insurance:Mathematics and Economics,2006,39(2):193-217
[8]WANG S S.A class of distortion operations for pricing financial and insurance risks [J].Journal of Risk and Insurance,2000,67(1):15-36
[9]WANG S S.A universal framework for pricing financial and insurance risks [J].ASTIN Bulletin,2002,32(2):213-234
[10]LIN Y,COX S H.Securitization of catastrophe mortality risks [J].Insurance:Mathematics and Economics,2008,42(2):628-637
[11]韦艳华,张世英.Copula理论及其在金融分析上的应用[M].北京:清华大学出版社,2008
[12]秦学志.金融工程理论与应用研究[M].大连:大连理工大学出版社,2005
[13]LEE S S,MYKLAND P A.Jumps in financial markets:a new nonparametric test and jump [J].The Review of Financial Studies,2008,21(6):2535-2563
[14]ERAKER B.MCMC analysis of diffusion models with application to finance[J].Journal of Business and Economic Statistics,2001,19(2):177-191
[15]CHERUBINI U,LUCIANO E,VECCHIATO W.Copula Methods in Finance [M].New York:John Wiley &Sons,2004
