变厚度叶片对离心压缩机结构强度和性能影响

孙 涛， 王 毅， 王 晓 放＊， 谢 蓉， 马 震 岳

（1.大连理工大学 海洋能源利用与节能教育部重点实验室，辽宁 大连 116024；2.大连理工大学 水利水电工程研究所，辽宁 大连 116024）

0 引 言

离心压缩机由于结构紧凑、工艺性好及可靠性高，在国民经济各部门中占有重要地位.目前，离心压缩机向大流量、高压比和高效率方向发展[1]，但是机组的大型化也给设计、制造、运行寿命和可靠性评估等带来了一系列问题，尤其是运行安全隐患显得较为突出[2].叶轮是离心压缩机及百万千瓦级核主泵等大型旋转机械的核心部件，其性能直接影响到运行的安全性与可靠性.特别对大型核主泵，结构更庞大，且要求其在大流量、高温、高压、高辐射环境中具有优秀的水力特性和超长使役寿命，这对离心旋转叶轮的设计提出了新的要求和挑战.

迄今为止，国内外关于离心压缩机流场计算的文献较多，主要的研究方向包括叶片前缘形状[3、4]、叶顶间隙[5、6]及进口导叶[7]等因素对叶轮气动性能的影响，但是研究叶片厚度分布对叶轮性能影响的文献少见[8].即使研究叶轮强度的文献也主要以轮盘形状优化[9、10]为研究方向，而关于叶片形状方面的文献未见报道.变厚度叶片研究文献很少，首先是因为叶片厚度的改变对叶轮结构强度和气动性能的影响较复杂，因而实际设计制造的大流量压缩机三元叶轮主要采用等厚度叶片；其次考虑到技术专利等因素，针对压缩机结构可靠性的核心技术资料罕有发表.

本文以国内某大流量离心压缩机首级叶轮为原型，针对应用较广的等厚度叶片的闭式叶轮，提出变厚度叶片的闭式叶轮的设计思想.在原始叶型数据的基础上，运用CAD软件Solidworks进行9种变厚度叶片的叶轮模型的建立，使用大型有限元软件ANSYS进行叶轮静态应力分析，利用计算流体动力学软件CFX进行叶轮内部流场分析，集中讨论变厚度叶片的闭式叶轮的结构强度与气动性能的变化规律，以期为大流量离心压缩机及大型核主泵的结构优化设计提供参考依据.

1 实体模型的建立

本文主要运用Solidworks建立所需要的9种闭式叶轮模型.叶片为前倾后弯式，其前缘与后缘均是椭圆形状（长短轴之比是3）.图1是叶轮I的几何模型的3个视图，从图中可以看出叶片、轮盘和轮盖的形貌.

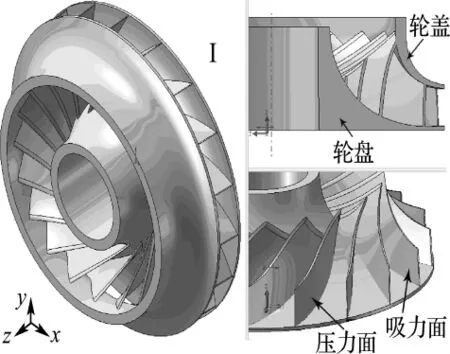
图1 叶轮I的几何模型Fig.1 Geometric model of the I impeller

9种叶轮不同的参数是叶片厚度.图2是9种叶轮叶片厚度变化曲线，表明了从前缘到后缘，叶片法向厚度的变化趋势.图中纵坐标为叶片法向厚度值（h），横坐标为叶片从前缘到后缘的相对弧长（x/l）.可知叶轮G是等厚度叶片（叶轮原型）、A～F是后缘厚度较大的叶轮、H和I是后缘厚度较小的叶轮.图3和4是9种叶轮的叶片实体几何模型.

2 有限元分析

2.1 定义材料特性与边界条件

图2 叶片厚度比较Fig.2 Comparison of the blades thickness

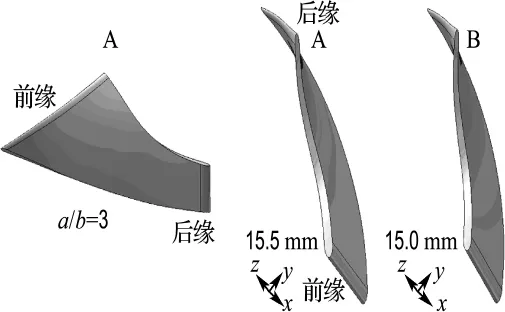
图3 叶轮A和B的叶片几何模型Fig.3 Blade geometric models of the A and B impellers

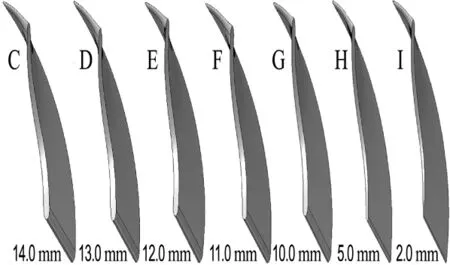
图4 叶轮C～I的叶片几何模型Fig.4 Blade geometric models of the C－I impellers

ANSYS中定义叶轮的材料特性：弹性模量为200GPa，泊松比为0.3，密度为7 800kg/m3.因为叶轮与轴采用过盈约束，故轮盘前端面取全约束，叶轮的内径处周向位移被约束.压缩机或核主泵运行时，离心力是叶轮最主要的应力，因此在用ANSYS进行叶轮静应力分析时，忽略气动力（由本文叶轮流场计算可知，气动力约为0.1 MPa），只考虑离心力.在ANSYS惯性荷载项中，设置叶轮的工作转速为3 820r/min.

2.2 网格划分

对于有限元分析而言，网格划分的好坏直接影响到计算的精度和速度.由于叶轮几何模型的复杂性，如叶片扭曲较大，叶轮I叶片最薄处达到2.0mm，本文采取ANSYS智能尺寸控制法，通过控制网格划分水平值和网格扩张系数，人工控制网格的大小和疏密分布.智能网格划分方法主要通过指定所有边线的份数来决定单元的尺寸，它可以考虑到线的曲率、单元阶次等特征.为了获得较好的计算精度，采用二次四面体单元（92号单元），能更好地划分出不规则形状的网格，较准确地模拟叶片表面的扭曲程度.

但是，采用更高阶的单元给曲线划分单元网格时，ANSYS会发出警告，甚至发出由于单元扭曲变形超过单元允许范围而引起网格划分失败的信息.其原因是：由于模型表面单元的弯曲程度过大，部分中节点偏离了自身位置，影响了网格的稀疏程度.本文采用智能网格划分时，ANSYS都会发出警告.经过尝试不同的智能网格划分以及对计算结果的综合分析，最终把警告网格数的百分比控制在0.4%以下.9种叶轮网格总数为150 000～350 000.图5是叶轮I的有限元模型，网格总数253 834，其中警告网格数607，约占0.24%，符合计算精度要求.

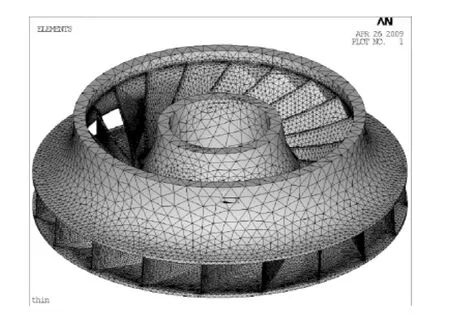
图5 叶轮I的有限元模型Fig.5 Finite element model of I impeller

2.3 计算结果与分析

本文以等厚度叶片的叶轮G为界限把9种叶轮分成两组，即组1：叶轮G～A，组2：叶轮G～I，通过观察最大von Mises应力值及其位置，进行计算结果分析.表1给出了叶轮的最大von Mises应力值，图6、7和8分别是叶轮A、D和G的应力分布云图.

对于组1，按照叶轮由G到A的顺序分析，即叶片厚度从等厚度到后缘厚度逐渐变大这一过程，最大von Mises应力值的变化具有一定规律性.以叶轮G的应力值为参考点，随着叶片后缘厚度的增加，在G－F－E－D过程中最大应力呈增加趋势，但是在D－C－B－A过程中最大应力呈下降趋势.而且，叶轮A～F的最大应力均位于出口的轮盘处，而叶轮G最大应力位于进口的轮盖处.因此，随着叶片后缘厚度的增加，最大应力值按照先增加后下降的规律变化.由表1可知，叶轮A与叶轮G相比较，最大von Mises应力值下降了15%，即叶片后缘厚度适当的增加对提高叶轮的强度是十分有利的.

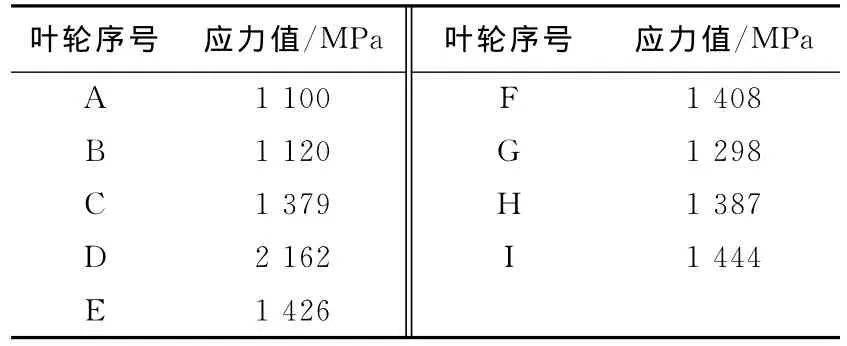
表1 叶轮的最大von Mises应力值Tab.1 Maximal von Mises stress of impellers

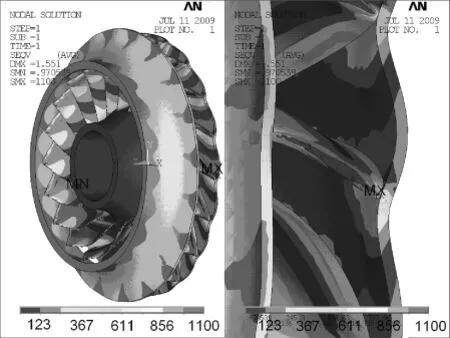
图6 叶轮A的应力分布云图Fig.6 Stress contour of A impeller

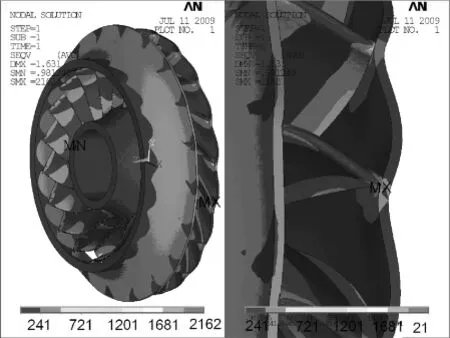
图7 叶轮D的应力分布云图Fig.7 Stress contour of D impeller

图8 叶轮G的应力分布云图Fig.8 Stress contour of G impeller

对于组2中的叶轮G～I，叶片厚度从等厚度到后缘厚度逐渐变小这一过程，最大von Mises应力值呈逐渐增大的趋势.而且，3种叶轮的最大von Mises应力均位于进口的轮盖处.通过计算可知，叶轮I比叶轮G的最大von Mises应力增加了11%.因此，对于等厚度叶片的叶轮，如果减小后缘的厚度，就会降低叶轮的结构强度.

通常，叶片厚度的增加会提高叶轮的强度，这对于等厚度叶片是正确的.作者曾对等厚度叶片按照每增加1mm的厚度进行分析，从而得到最大von Mises应力的变化规律，发现叶片厚度的增加能显著地提高叶轮的强度.但是，对于本文所研究的9种变厚度叶片的叶轮，最大von Mises应力值的变化不是按照线性变化.组2的分析结果与叶片厚度的增加会提高叶轮的强度相符合，这说明减薄后缘厚度会对叶轮结构强度产生不利影响.组1分析表明，增加后缘厚度并不一定会增强叶轮的强度，最大von Mises应力值按照先增加后下降的规律进行变化.但是，当叶片后缘厚度增加到合适的数值时，能够显著地提高叶轮的结构强度.

3 气体动力学分析

由于叶片厚度的变化会对叶轮流场产生很大影响，本文运用CFX软件对其中的5种叶轮进行气体动力学计算研究.为了便于分析，所取的5种叶轮分别是B、E、G、H和I，即一个等厚度叶轮G、两个厚后缘叶轮B和E、两个薄后缘叶轮H和I.

模拟类型为稳态模拟，采用k－ε湍流模型.工作介质为空气（理想气体）.边界条件：给定轴向进气，进口总温293K和总压1×105Pa，出口给定质量流量110 000m3/h，转动壁面给定转速3 820 r/min，其他壁面转速为零，壁面处满足无滑移条件.当残差达10－4时，计算结束.每种叶轮的单通道网格数约为25×104.

对离心压缩机某一级来说，相对该级中其他静止元件，叶轮的效率是最高的，在保证相同的叶片进口角、出口角、叶片个数和叶轮内外径的前提下，叶片形状的优良与否直接关系着叶轮效率的高低.以下是应用CFX软件计算得到的5种不同叶片形状的叶轮内部的流动结果.气体动力学性能参数计算结果汇总于表2，子午面压力分布见图9，50%叶高处周向平面熵分布见图10，50%叶高处周向平面相对马赫数分布见图11.

总体上看，5种变厚度叶片的叶轮内部流动很相似，但从叶轮叶片相对马赫数分布可以看出，相对而言，叶轮B的流场分布最为均匀，低速区范围最小，速度梯度也最小，叶轮出口的流场沿宽度分布也最为均匀，这也是叶轮B的多变效率最高的主要原因所在，其中叶轮B与叶轮H相比，等熵效率提高了3%.其次是叶轮E，这可能是因为叶片厚度沿翼展方向从中间到出口相应增加以后，在一定程度上减小了原设计叶轮叶片流道的扩张度，因而减小了扩张损失，所带来的负面效果就是相应减弱了叶片的扩压能力.

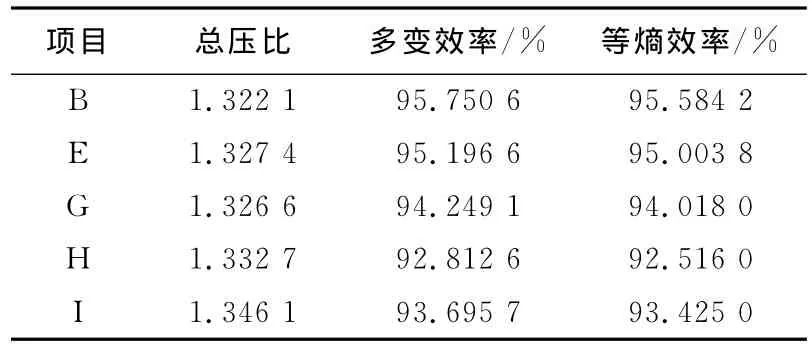
表2 气体动力学性能参数计算结果Tab.2 The results of aerodynamic performance parameters

图9 子午面的压力分布Fig.9 Stress contour of meridian plane

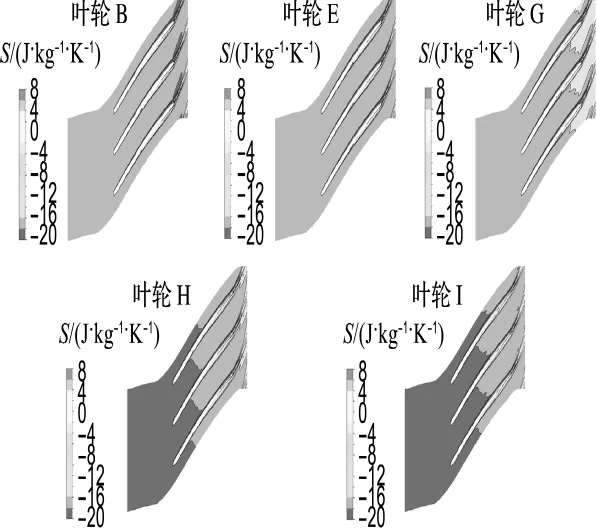
图10 50%叶高处周向平面的熵分布Fig.10 Contour of entropy at 50%span in circumferential direction

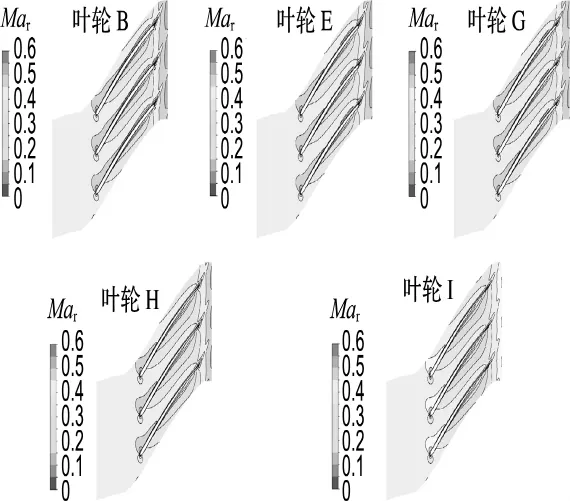
图11 50%叶高处周向平面相对马赫数分布Fig.11 Contour of relative Mach number at 50%span

从叶轮子午面的压力分布可以看出，5种形式的叶轮压力从进口到出口都是均匀增加的，而叶轮I的压力升高最为均匀，且出口压力沿宽度分布最为均匀，因而叶轮I的总压比是5种形式的叶轮中最高的，这可能是由于叶片厚度沿翼展方向从中间到出口相应减薄后，在一定程度上增大了流道的扩张度，从而提高了叶片流道的扩压能力，但反过来却增加了流道的扩张损失，因此叶轮I的效率较低.

从叶轮叶片在周向平面的熵分布可以看出，5种形式的叶轮，其熵的分布从叶根到叶顶都是逐渐增加的，且在叶片的吸力面和叶片出口处，熵增明显，这是由于叶片在吸力面上的流动有脱离现象发生，在出口处有尾迹损失.分析叶片B、E的整体熵分布，从叶根到叶顶的熵增幅度比较小，说明叶轮叶片沿叶高方向的流动损失较小，因此，这两种形式的叶轮效率较高.

综上所述，对每一种离心叶轮而言，其叶片型线从进口到出口的厚度变化应该有一个最佳值，以保证叶轮的效率和总压比的变化相互和谐，达到相对最佳值.对本文研究的叶轮而言，从气体动力学角度出发，相对于其他叶轮，叶轮G的多变效率和总压比都是较高的，即等厚度叶片可以使叶轮的效率和总压比达到折中的水平.同时，通过计算分析可知，随着叶片后缘厚度的增加，叶片流道的扩张度开始变小，进而降低了扩张损失，最终使得叶轮的效率增加，但是此时会导致总压比略有下降（由表2可知总压比的下降程度相对较小）.因此，在满足总压比的情况下，对叶片后缘进行适当的加厚，可以较显著地提高叶轮效率.

4 结 论

（1）从结构强度的角度出发，一般而言，叶片厚度的增加能明显地提高叶轮结构强度.因此，减薄叶片后缘厚度对叶轮的强度十分不利.但是，随着叶片后缘厚度的增加，叶轮的最大von Mises应力值按照先增加后下降的规律变化.因此，当叶片后缘厚度增加到合适的数值时，才能显著地提高叶轮的结构强度.

（2）从气体动力学的角度出发，与变厚度叶片相比，等厚度叶片可以使叶轮的效率和总压比达到相对折中的水平.由分析可知，随着叶片后缘厚度的增加，叶片流道的扩张度开始变小，进而降低了扩张损失，最终促使了叶轮效率的增加，但是此时会导致总压比略微下降.因此，在满足总压比的情况下，对叶片后缘进行适当的加厚，既可以提高叶轮结构的安全性，又可以明显地提高压缩机叶轮的效率.

（3）变厚度叶片的研究分析为大流量离心压缩机及大型核主泵等旋转机械的叶轮结构设计提供了重要的参考依据.

[1] 吴承伟，关振群，郭杏林，等.大型离心压缩机叶轮叶片疲劳可靠性分析[J].装备制造技术，2008（8）：1－3

[2] 刘 军.大流量离心压缩机首级叶轮强度分析及结构改进设计研究[D].大连：大连理工大学，2009

[3] SAUER K，MULLER R，VOGELER K.Reduction of secondary flow losses in turbine cascades by leading edge modifications at the endwall[J].ASME Journal of Turbomachinery，2001，123（2）：207－213

[4] ZESS G A，THOLE K A.Computational design and experimental evaluation of using a leading edge fillet on a gas turbine vane [J].ASME Journal of Turbomachinery，2002，124（2）：167－175

[5] CHEN G T，GGEITZER E M，TAN C S，etal.Similarity analysis of compressor tip clearance flow[J]. ASME Journal of Turbomachinery，1991，113（2）：260－271

[6] HOFFMA N W H，BALLMAN J.Some aspects of tip vortex behavior in a transonic turbocompressor[R]//ISABE Paper.Bangalore：International Society for Air Breathing Engine，2003

[7] CHEN Y N，HAGELSTEIN D，KASSENS I，etal.Effect of the decaying overshoot of the Rankine vortex on the axial flow field behind the inlet guide vane of centrifugal compressors[R]//ASME Paper，2000－GT－427.New York：AMSE，2000

[8] 王晓锋，席 光，王尚锦.叶片厚度分布对超窄流道离心叶轮性能的影响[J].西安交通大学学报，2004，38（9）：975－979

[9] 雒 婧，席 光，郭常青.离心叶轮的应力数值分析与结构优化[J].流体机械，2004，32（11）：8－10

[10] 关振群，罗阳军，王学军.离心式叶轮三维参数化形状优化设计方法[J].机械强度，2006，28（6）：833－838