利用欧氏距离函数评估海河流域暴雨灾害*

吴振玲，史得道，吕江津，杨 煜，汪 靖

(1.天津市气象台，天津300074;2.天津市气象局科技发展处，天津300074;3.天津市气象局，天津300074)

利用欧氏距离函数评估海河流域暴雨灾害*

吴振玲1，史得道1，吕江津2，杨 煜3，汪 靖1

(1.天津市气象台，天津300074;2.天津市气象局科技发展处，天津300074;3.天津市气象局，天津300074)

考虑气象数据的特点和灾后评估的时效性，针对暴雨灾害的平均降水强度、最大降水影响范围、持续时间，利用欧氏距离等数学方法，研究了海河流域暴雨灾害的气象评估模型。利用该评估模型对1960－2008年间的海河流域暴雨进行了评估，结果表明，等级划分合理，所评估的暴雨气象等级级别与海河流域历史上对应的洪灾事件影响程度非常吻合。

暴雨灾害;欧氏距离;评估向量;评估模型;决策服务;海河流域

0 引言

由于海河流域地域广阔，跨越内蒙古、辽宁、山西、河北、河南、山东六省和北京、天津两个直辖市(图1)，因此海河流域暴雨既是海河流域水资源的重要构成，也是产生海河流域洪涝灾害的重要原因［1］。每年夏季，海河流域都是全国重点防汛的流域之一，各级政府及其相关职能部门十分重视海河流域的暴雨灾害天气。因此，建立海河流域暴雨灾害评估模型，对准确发布海河流域暴雨灾害的天气预警，做好暴雨发生前期的准确预评估及突发性暴雨灾害的及时后评估，有着重要的意义。

国内一些专家学者，利用统计分析等多种方法建立灾害评估模型［2－7］，在暴雨、洪水、地质滑坡等自然灾害风险评估方面进行了尝试［8－12］。大部分的气象灾害评估方法都比较注重受灾人群(包括伤亡人口)、受灾面积、受灾毁损程度、经济损失等灾害发生后的灾情和经济评估，忽视了针对灾害事件本身的强度、影响范围、持续时间可能产生的危害气象等级评估。周月华［13］等人对暴雪过程提出了一个综合指数统计方案，但对暴雨评估的适用性不强。由于灾情和经济评估指标受不同区域的经济发展、公共设施建设、生产及生活方式、灾后社会调查广度、信息汇总时间滞后等影响，存在着不确定性，影响气象灾害发生后的快速评估，同时不利于气象部门有效地开展气象灾害的预报预警及决策服务。尤其海河流域暴雨事件的预评估，关系到各级政府合理利用降水资源、防洪防涝等系列应对措施，因此，有必要在研究暴雨灾害历史事件的灾害特点基础上，建立海河流域暴雨事件气象评估模型，满足海河流域储水、泄洪、防御等决策服务需求，切实做好减灾防灾的气象服务保障。陈艳秋［14］等人采用单纯气象评估模型实现了辽宁暴雨事件的灾前、灾后评估，在实际服务中已取得成效。

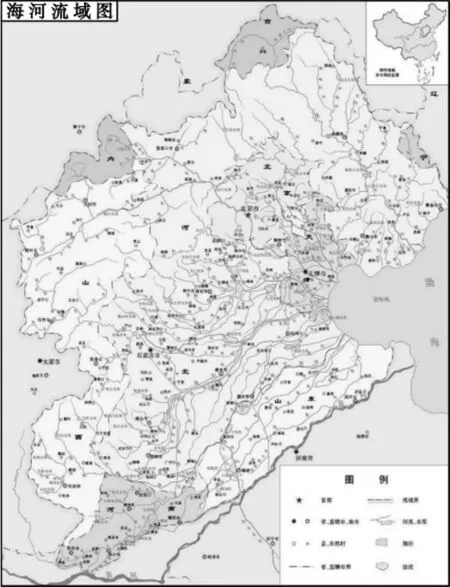
图1 海河流域行政区域图

目前，天津海河流域灾害性降水评估仍然使用单一的降水总量指标进行降水分级分析，对海河流域区域暴雨事件的气象定义比较模糊，对暴雨本身的强度特征、影响范围、持续时间的分析主要以定性为主，缺乏相对完整的量化评价因子的分析方法和评估模型，无法快速地提供海河流域暴雨灾害的气象风险等级评价，一定程度上影响区域气象灾害联防响应的及借鉴陈艳秋［14］等人的辽河暴雨气象评估方法，本文利用近60年的气象资料，采用欧氏时性和气象服务的社会效益。

距离方法建立了海河流域区域暴雨事件气象评估模型，对海河流域区域暴雨事件进行了气象等级评估和分析。

1 资料

选用1960－2008年6－9月海河流域165个气象观测代表站的24 h降水量作为区域暴雨事件评估统计的基本资料。

1.1 选取评估代表站

根据现有实时资料业务运行系统和暴雨评估的实际需求，按照海河流域8大河系区域划分的地理位置、所占面积，共选取了165个气象观测站点作为海河流域暴雨评估代表站，这些观测站点分布间距相当，实时观测资料传输稳定，1960－2008年期间，气象观测记录不少于30年。其中，滦河水系有23个代表站点，北三河系26个代表站点，永定河系有29个代表站点，大清河系有33个代表站点，子牙河系有58个代表站点，漳卫河系有50个代表站点，徒骇马颊河系有25个代表站点，海河干流系有10个代表站点。

1.2 区域暴雨样本选取

考虑海河流域总面积达31.8万km2，因此，一次降水过程中，如果海河流域评估代表站中，有13个或以上观测站点的24 h降水量达到50 mm暴雨标准的，就记为一次流域区域暴雨事件。按照上述区域暴雨定义，从1960－2008年海河流域汛期6－9月的24 h降水量资料中，可提取区域暴雨样本为244个。

2 评估原理简介

欧氏距离评估方法的基本思路是，利用欧氏空间和向量的概念，将多元评估指标和多级评估标准转换为多维空间中的多个标准评估向量点，待评估的多元暴雨指标看作是多维空间中的任意一个向量点，通过计算分析被评估向量与多个标准评估向量点之间的距离，完成暴雨灾害过程的等级评估。

2.1 确定区域暴雨评估标准

根据前期流域暴雨资料分析，选取n个评估特征量x1，x2，x3，…，xn作为评估指标，并将每个区域暴雨评估指标分为5个评估等级，即5、4、3、2、1级，暴雨灾害严重程度随数字减小而增加。

根据每个评估特征量的频率分布特征，将1年一遇、2年一遇、5年一遇、10年一遇、100年一遇对应的分位数值x0n、x2n、x5n、x10n、x100n，定义为5级、4级、3级、2级、1级的评估阈值。

n个评估特征量、5个等级标准评估阈值形成了一个n行、5列的等级标准评估指标数据集合，即等级标准评估指标矩阵X0(简称等级标准矩阵)。

2.2 建立等级评估矩阵

2.2.1 无量纲等级标准矩阵

将X0矩阵的每行第5列向量作除数，进行各行运算，那么等级标准矩阵X0就转化成初始无量纲等级标准矩阵A*=［a*ij］，(i=1，2，3，…，n，j=1，2，3，4.5)。由于a8i5=1，所以，

式中:a*ij就是第i个指标、第j级标准与100年一遇标准的比值。

2.2.2 计算权重系数

首先，利用式(3)、(4)计算矩阵A*的各行向量的标准差S*i与均值μ*i。其次，利用式(5)计算变异系数w*i。

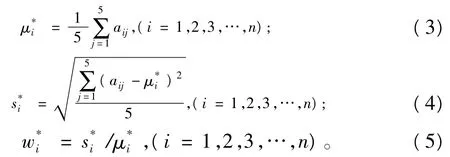
变异系数w*i可以代表各指标的权重［15］。对变异系数归一化得到各指标的权向量为:

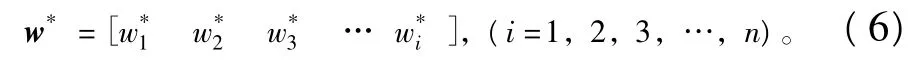
2.2.3 调整权重系数

权重系数的调整步骤应在2.3节后面进行。除分析评估特征量对暴雨灾害形成的作用以外，选取多个典型暴雨灾害进行试评估，通过评估结论和历史资料对比，将调整权重系数为:

方法是，在原有5级等级标准评估阈值上加或减一个常数，即将等级标准评估指标矩阵(1)X0中的每行向量加或减一个常数，得到一个等级标准评估矩阵 X=［xij］，(i=1，2，3，…，n，j=1，2，3，4.5)，

这样的调整不会改变资料集的分布特征。X矩阵中，xij代表调整后的最终等级评估标准。

2.2.4 无量纲等级评估矩阵

利用上述矩阵(2)A*的转化方法将X矩阵转换为无量纲等级评估矩阵A，A中的5列数值代表5级标准评估向量。

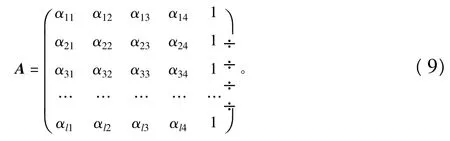
2.3 欧氏距离等级评估

2.3.1 确定欧氏空间评估点集

当评估一次暴雨事件时，根据选取的n个评估特征量(或n个评估指标)的定义，按照矩阵(6)中的最终等级评估标准xij的计算方法，可以求出评估指标 ξ1，ξ2，ξ3，…，ξv，经式(8)的无量纲处理后，得到一组被评估指标。

因而组成被评估向量 Y=(y1，y2，y3，…，yn)。

n维欧氏空间是由一个点的集合组成的，利用这个概念，将n×5的A矩阵中各列向量看作是n维空间中的5个评估向量点，第1列代表第5级标准评估向量点，第2列代表第4级标准评估向量点，以此类推，第5列代表第1级标准评估向量点。

将式(8)计算得到的被评估向量Y看作是n维空间中的一个被评估向量点，那么5个标准评估向量点和1个被评估向量点就组成了n维欧氏空间的评估点集。

2.3.2 欧氏距离评估模型

欧氏距离等级评估的思路是，求解被评估向量点与5个标准评估向量点之间的欧氏距离，利用距离大小来判断被评估向量与标准评估向量的相近程度，欧氏距离越小，表示被评估向量点与某一个标准评估向量点越接近。

根据n维空间中两点之间欧氏距离(Euclidean distance)的计算公式(11)，计算Y到矩阵A中各列向量的距离:

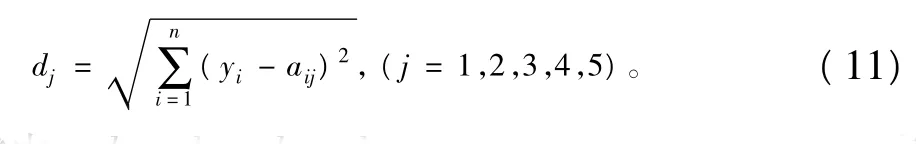
式中:d1，d2，d3，d4，d5分别代表被评估向量点到第5级标准评估向量点、第4级标准评估向量点、第3级标准评估向量点、第2级标准评估向量点和第1级标准评估向量点的距离当被评估向量点与某一个标准评估向量点距离最短时，就认定该标准评估向量代表的等级是此次暴雨评估的等级。

3 评估方法业务应用

3.1 暴雨评估指标

河北省地理研究所侯明［1］对海河流域历史上出现的典型暴雨灾害事件的研究发现，引发流域洪涝灾害的暴雨强度都与单日暴雨平均降水量、区域暴雨降水量极值、降水覆盖范围和持续降水日有着紧密的联系，所以，选取了以下4个区域暴雨评估特征量，以表征海河流域暴雨事件的强度。

(1)平均降水量

评估区域内，暴雨观测代表站点的24 h暴雨平均降水量Ra，表征单日区域暴雨平均降水强度。

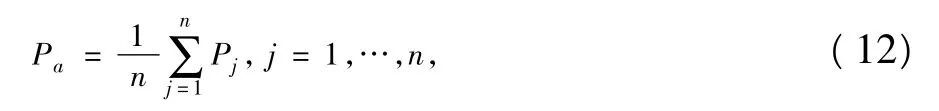
式中:n为海河流域内降水量达到暴雨标准的代表观测站个数;Pj为其中第j个观测站点在被评估事件中的总降水量(mm)。

(2)最大降水量

暴雨评估区域内出现的最大24 h降水量，表征单日区域暴雨最大降水强度。

式中:max()为取最大值函数符号，n为海河流域内降水量达到暴雨标准的代表观测站个数，P24j为第j个观测站点在暴雨过程中最大的24 h观测降水量(mm)。

(3)降水覆盖率

出现暴雨的观测代表站点个数与海河流域内观测站点总数比值，表征暴雨影响的范围

式中:n为海河流域内降水量达到暴雨标准的代表观测站个数;N为海河流域区域内观测站点总数(个)。

(4)降水持续时间

区域暴雨出现日及之后在相同区域内连续出现7个及以上站点的降水量达到或超过25毫米的日数。

式中:m为暴雨事件中连续出现7站以上降水量≥25 mm的日数。

3.2 确定评估向量

3.2.1 等级标准评估阈值确定

将平均降水量和降水量极值进行“取对数后再开平方”的数学处理，以缩小4个评估指标的数值量级差别。按照2.1节中的方法，分析所选取的评估指标频率分布特点，剔除数据序列异常值后，分别计算5等级评估阈值，得到等级评估标准。表1所示为海河流域区域暴雨5等级评估标准。

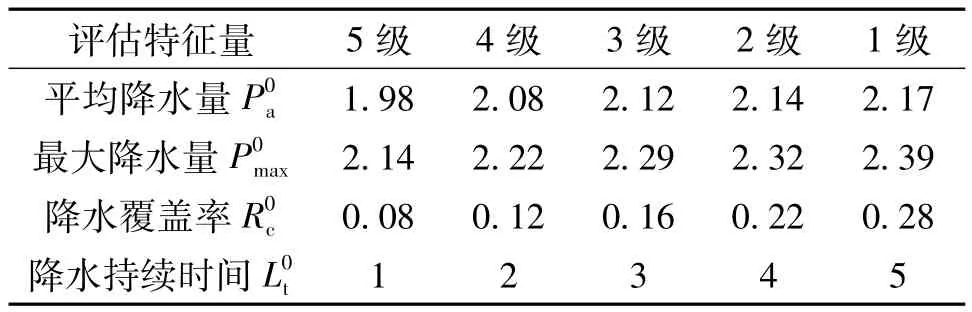
表1 海河流域区域暴雨5等级评估标准

因此，得到等级标准矩阵为:

3.2.2 计算权重系数

无量纲处理后，得到无量纲化的等级标准矩阵为:

利用式(3)、(4)、(5)计算权重系数得到权向量:

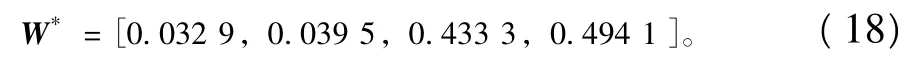
3.2.2 调整权重系数

根据实际暴雨个例分析经验，平均降水量和最大降水量的权重系数计算结果明显偏小，按照

2.2.3 节中的调整方法调整权重系数，当矩阵(16)中的四行数组按照式(19)进行转换时，

权向量刚好调至实际暴雨预报经验认可的范围W=［0.5，0.2，0.1，0.2］。 (20)此时的5级标准评估指标转换矩阵X是

3.2.4 确定5个标准评估向量点

对矩阵X无量纲处理，其无量纲转换等级标准矩阵A为:

把A矩阵中1到5列数组分别代表4维空间中5个标准评估向量点，也就是4维空间中的5级、4级、3级、2级、1级标准评估向量点。

3.2.5 计算被评估向量点

选取2000年7月5日暴雨为评估个例，计算被评估向量，共有以下三步骤，计算结果详见表2。

(1)数学处理。将平均降水量和最大降水量的原拾数据取对数再开平方，计算降水覆盖比率和降水持续时间的原值就是R*c，L*t。

(2)指标转换。利用式(19)分别计算 Pa，Pmax，Rc，dt。

(3)无量纲化。利用式(8)进行运算，即Pa/0.17，Pmax/0.43，Rc/0.63，Lt/7.2。

表2 被评估向量计算值

表2中的最后一列无量纲数值组成了被评估向量为

3.3 暴雨等级评估

利用欧氏距离公式(9)计算被评估向量点Y到矩阵A中5个标准向量点的距离，结果一维矩阵D:

矩阵D中，第4列数据最小，说明被评估向量Y与第4列的第2级标准评估向量的欧氏距离最近，因此，判断该次暴雨的评估气象等级为2级。

3.4 暴雨等级评估检验

应用此评估方法，对1960－2008年期间海河流域所有区域性暴雨历史个例进行验证评估。评估统计结果如表3所示。近50年内，244个区域性暴雨样本中，评估为1级的100年一遇的区域暴雨占3.28%，2级10年一遇的占4.51%。

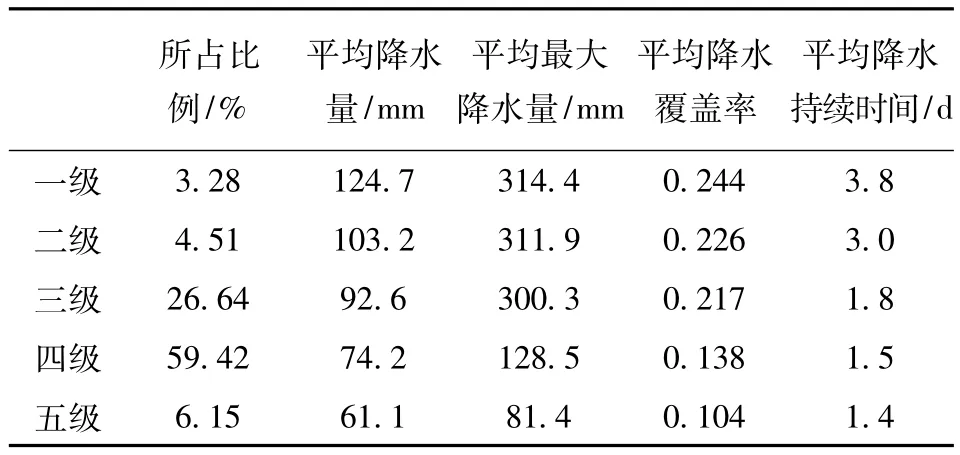
表3 海河流域暴雨灾害等级评估统计结果

评估结果表明:

(1)欧氏距离评估等级比较合理。表3显示，评估后，100年一遇的1级暴雨4项特征指标值最大，1年一遇的5级暴雨4项特征指标值最小，即随着暴雨严重程度的降低，其平均降水量、平均最大降水量、平均降水覆盖率和平均降水持续时间逐级依次减少。

(2)暴雨灾害历史评估等级准确。通过评估暴雨个例的灾情记录对比，该评估模型评估的区域暴雨气象等级与海河流域历史上对应的洪灾事件影响程度非常吻合。其中评估为1级(100年一遇)的暴雨灾害有8次，有5例样本来自造成全流域大范围的洪涝灾害的1963年8月3－7日连续性暴雨和96年8月3－5日特大暴雨过程，其他3例样本分别来自1960年28－31日、1984年9－10日和1994年7月12－13日。评估为2级11次暴雨样本，也都来源于海河流域分河系上造成明显的洪灾事件，如1962年7月22－26日的暴雨造成1949以来滦河水系第1位大洪水，75年7月底之8月初、77年7月26－27日，84年8月等都造成了海河流域不同分河系的特大洪水事件。评估为3级的暴雨事件基本上是暴雨降水量比较大，降水持续时间比较短或降水覆盖率低、没有发生流域内河系的明显洪灾事件，局部地区可能会因地势原因，河系内流水量偏多。4～5级的暴雨事件，由于其覆盖范围较小，产生分支河系或整个流域的洪灾事件可能很小。

4 小结与讨论

4.1 欧氏距离评估方法的特点

欧氏距离暴雨评估方法实质上就是通过多维空间的聚类分析完成每次暴雨等级的评估。在海河流域暴雨等级评估应用中，将选取的平均降水量、最大降水量、降水覆盖率、降水持续时间4项评估指标和5级评估标准，看作是4维空间中的5个标准评估向量点，将任意一次暴雨过程看作是4维空间中的任一被评估向量点，通过求取被评估点与5个标准评估向量点间的距离，分析被评估向量与5个标准评估向量的相似程度，取距离最近的标准评估向量点所代表的暴雨等级作为暴雨评估等级。因此，评估模型确定后，评估过程简便易行。

4.2 该评估方法的可行性

(1)评估等级划分比较合理。

利用50年的降水统计资料，按照100年一遇、10年一遇、5年一遇、2年一遇、1年一遇来划分暴雨的5级评估标准，对区分暴雨灾害的严重程度有较好的表征意义。评估结果显示，暴雨灾害严重程度和其评估的平均降水量、平均最大降水量、平均降水覆盖率和平均降水持续时间的大小有较好的一致性，如评估为1～2级暴雨灾害维持时间基本在3 d以上。平均降水量超过100 mm。

(2)评估结论具有决策指导意义

利用欧氏距离建立的海河流域暴雨评估模型，其暴雨等级评估结论与历史洪涝灾害特点十分吻合。1级暴雨容易引发全流域洪涝灾害;2级暴雨容易引发海河流域分河系的洪灾事件;3级暴雨容易引起局部地区河道流量偏高;4～5级的暴雨不易引发分支河系或整个流域的洪灾事件。因此，在暴雨发生前，可以利用该模型对暴雨进行预评估，对合理利用海河流域暴雨水资源或加强洪涝灾害预防等决策服务提供科学的气象依据和合理化建议，即预评估为1、2级暴雨时，提示提前做好海河流域的洪涝灾害预防;预评估为3级暴雨时，提示大部分地区可储存降水，部分低涝地区注意洪涝灾害;预评估为4、5级暴雨时，提示注意雨水储存，无洪涝危险。

［1］侯明．海河流域暴雨及分区治理对策［J］．自然资源，1993(5):51－57．

［2］王博，崔春光，彭涛，等．暴雨灾害风险评估与区划的研究现状与进展［J］．暴雨灾害，2007，26(3):281－286．

［3］于文金，闫永刚，吕海燕，等．基于GIS的太湖流域暴雨洪涝灾害风险定量化研究［J］．灾害学，2011，26(4):1－7．

［4］袭祝香．吉林省重大暴雨过程评估方法研究［J］．气象科技，2008，36(1):78－81．

［5］于庆东，沈荣芳．自然灾害综合灾情分级模型及应用［J］．灾害学，1997，12(3):12－17．

［6］李吉顺．关于台风、暴雨灾害评估工作的探讨［J］．中国减灾，1993，3(3):32－34．

［7］赵琳娜，吴昊，田付友，等．基于TIGGE资料的流域概率性降水预报评估［J］．气象，2010，36(7):133－142．

［8］陈报章，仲崇庆．自然灾害风险损失等级评估的初步研究［J］．灾害学，2010，25(3):1－5．

［9］邱向荣，袁仁茂，许伟文．公路边坡灾害危险性预测模糊综合评判法［J］．水土保持研究，2003，10(3):26－28，36．

［10］刘伟东，扈海波，程丛兰，等．灰色关联度方法在大风和暴雨灾害损失评估中的应用［J］．气象科技，2007，35(4):563－566．

［11］李祚泳，邓新民．自然灾害的物元分析灾情评估模型初探［J］．自然灾害学报，1994，3(2):28－33．

［12］魏一鸣，万庆，周成虎．基于神经网络的自然灾害灾情评估模型研究［J］．自然灾害学报，1997，6(2):1－6．

［13］周月华，郭广芬．基于多指标综合指数的灾害性天气过程预评估方案［J］．气象，2010，36(9):87－93．

［14］陈艳秋，袁子鹏，盛永，等．辽宁暴雨事件影响的预评估和灾后速评估［J］．气象科学，2007，12(6):626－632．

［15］胡守信，李柏年．基于MATLAB的数学实验［M］．北京:科学出版社，2004:81－83．

Evaluation of Heavy Rain Disaster in Haihe River Basin by Euclidean Distance Method

Wu Zhenling1，Shi Dedao1，Lü Jiangjin2，Yang Yu3and Wang Jing1
(1．Tianjin Meteorological Observatory，Tianjin 300074，China;2．Scientific and Technological Development Office of Tianjin Meteorological Bureau，Tianjin 300074，China;3．Tianjin Meteorological Bureau，Tianjin 300074，China)

In view of the specialty of the meteorological data and timeliness of the evaluation，HR disaster meteorological evaluation of the HRB is studied by Euclidean distancemethod after considering the averaged precipitation intensity，themaximum influence scope and its duration．The evaluationmodel is used for evaluating the HRB's HR during 1960～2008．The results show that the evaluated meteorological grades of HR concur with the influence of the flooding events ever occurring in HRB．

heavy rain disaster;Euclidean distance method;evaluation vectors;evaluation model;decisionmaking services;Haihe River Basin

P429

A

1000－811X(2012)03－0048－06

2011－11－30

2012－01－10

中国气象局新技术推广项目(CMATG2010Z09)

吴振玲(1963－)，女，天津人，高级工程师，研究方向为气象服务与应用气象．E-mail:wiselyyn@yahoo.com.cn