直驱式风力发电系统中TSMC的研究

王 硕，田立欣，黄殿君，盖国权

（1.内蒙古工业大学 内蒙古 呼和浩特 010080；2.内蒙古电力（集团）有限责任公司巴彦淖尔电业局 内蒙古 巴彦淖尔 015000）

风能是一种可再生的、无污染的绿色能源，所以风电的发展越来越受到人们的重视，各国都在大力发展本国的风电项目。直驱式风力发电系统也以其自身的独特优势受到越来越多科研工作者的重视，而在直驱式风力发电系统中的全功率变流器的地位是至关重要的，所以笔者讨论了将TSMC（双级矩阵变换器）用于直驱式风力发电系统中。TSMC器集合了矩阵变换器和传统的交-直-交变换器的优点，对TSMC的深入研究不仅对风力发电并且整个电力变换领域都有重要的意义。

1 TSMC用于直驱式风力发电系介绍

直驱式永磁同步风力发电系统，风力机直接与永磁同步发电机相连，不需要升速齿轮箱。首先将风能转化为频率和幅值均变化的交流电，然后通过电力电子变换装置变为恒幅恒频率的交流电接入电网。与现在普遍使用的双馈风力发电系统相比，由于采用风机与永磁同步发电机直接耦合，省去了齿轮箱，这样大大减小了系统噪声，降低了系统的控制难度，提高了系统的可靠性，延长了系统的使用寿命，降低了风力发电成本。并且随着全功率变流技术的快速发展，目前的风力发电系统正向无齿轮箱的直驱式永磁风力发电的趋势发展，而且已经在不同功率等级的风力发电系统中开始应用。直驱式永磁风力发电系统对变流装置要求较高，所以本文将TSMC应用于直驱是风力发电系统中，来得到性能更好的风力发电机组。系统的结构[1-2]如图1所示。

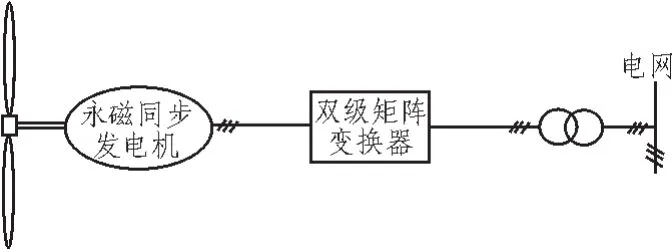
图1 TSMC用于直驱式风力发电系统结构图Fig.1 StructureofTSMCusedindirect-drivewindpowergenerationsystem

2 TSMC（双级矩阵变换器）

TSMC与传统的的交直交PWM变频器和矩阵变换器相比，首先，具有良好的输入输出性能、高输入功率因数，并且可以实现能量的双向传输；其次，直流环节不需要大电容，钳位电路简单；再次，整流级可以实现开关零电流换流，逆变级可以采用传统的矩阵变换器的换流方法，换流方法简单，提高了整体的可靠性；并且具有中间直流环节可以采用比较成熟的PWM控制，进一步降低了系统的控制难度。

TSMC的拓扑结构如图2所示，系统由18个IGBT组成，整流级由6组发射极相连的IGBT构成的双向开关组成，逆变级与传统的逆变器相同。

图2 TSMC拓扑结构Fig.2 Topology of TSMC

3 TSMC的调制方法

3.1 整流级的PWM调制

TSMC整流级的调制目标为：保证直流侧的输出电压始终为正，电压传输比为最大，并且输入功率因数为一[3-6]。

设三相输入电压为：

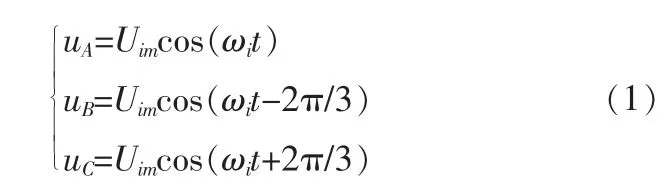
式中Uim为输入相电压的幅值，ωi为输入电压的角频率。为了便于分析整流级的调制原理，将一个周期的输入电压分成6等份，即六个扇区，每个扇区为π/3。如图3所示。

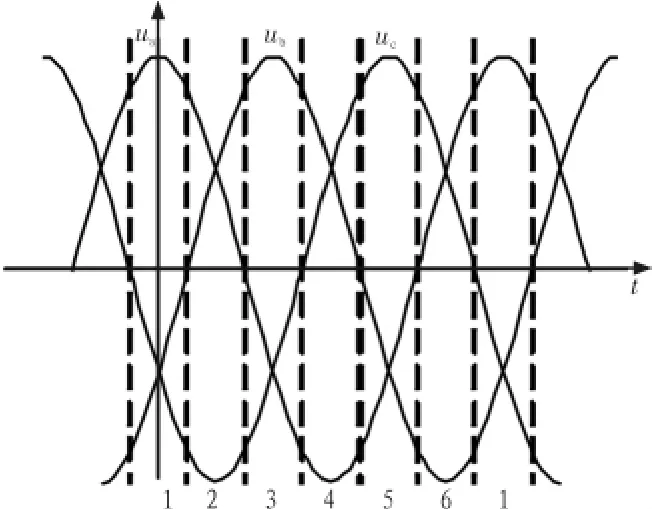
图3 整流级的扇区划分Fig.3 Voltage intervals of rectifier stage

每个扇区都有一个共同的特点，一相的电压绝对值最大，另外两相的极性与之相反。所以将每一个扇区分为两个时间段，在这连两个时间段内，保证电压绝对值最大的那相的上桥臂或下桥臂始终导通，另外两相的上下桥臂轮流导通。这样在一个扇区内就可以输出两个幅值最大的极性为正的电压矢量，并且不会出现零矢量。

下面以扇区一为例进行说明：在扇区一中A相电压始终为正且电压值最大，B、C两相电压极性与之相反。所以，为保证电压传输比为最大，在扇区一中A相始终导通，B相和C相轮流导通。 即第一段时间内 SAp1、SAp2、SBn1、SBn2导通，这时直流侧的输出电压udc=uAB=uA-uB，传递函数为

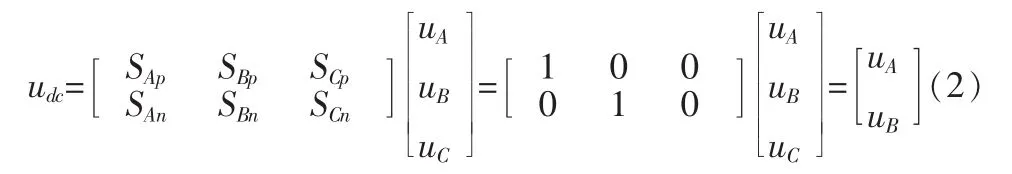
第二段时间内 SAp1、SAp2、SCn1、SCn2导通，这时直流侧的输出电压udc=uAC=uA-uC，传递函数为

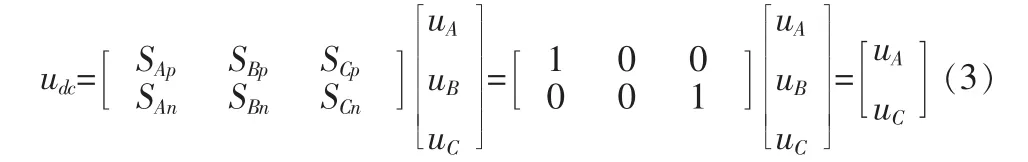
整流级调制的另外一个目的，要保持输入功率因数为1。仍以扇区一为例，直流侧的正极p在扇区一中始终连接在A相，B、C两相则轮流连接到直流侧的负极n。在一个PWM调制周期内，局部直流电流的平均值为i¯为定值，三相输入电流的局部平均值为i¯A、i¯B、i¯C。设两段时间的占空比分别为dAB、dAC，所以有

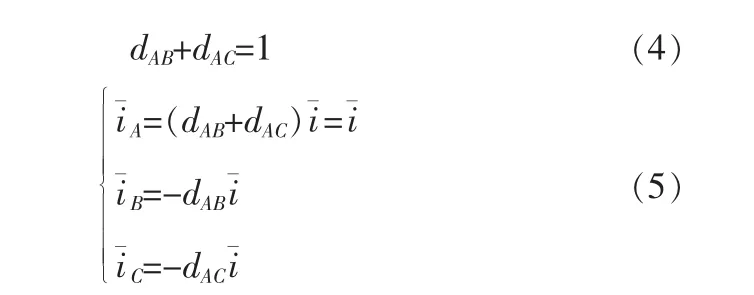
为保持输入功率因数为1，需使每相输入电流平均值的大小始终与同相电压成正比，所以

因此，第一段时间的占空比为

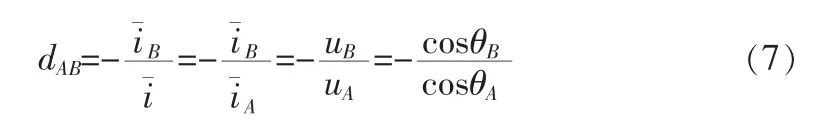
所以一个 PWM 调制周期内， 开关 SAp1、SAp2、SBn1、SBn2导通时间为：

式中，Ts为PWM调制周期。

第二段时间的占空比为

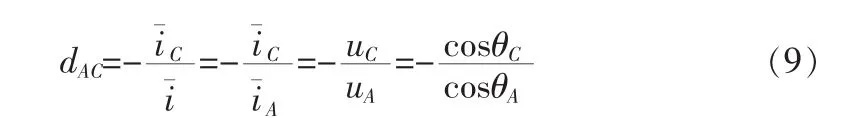
开关 SAp1、SAp2、SCn1、SCn2的导通时间为：

同理可得其他扇区的开关状态以及相应的占空比。所以一个PWM调制周期内的直流侧平均电压为

将式（1）、（7）和（9）代入式（11），得

同理可得其他调制周期内的局部平均电压为：

其中，cosθi=max（|cosθA|，|cosθB|，|cosθC|）。

3.2 逆变级的SVPWM调制

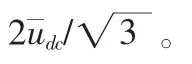
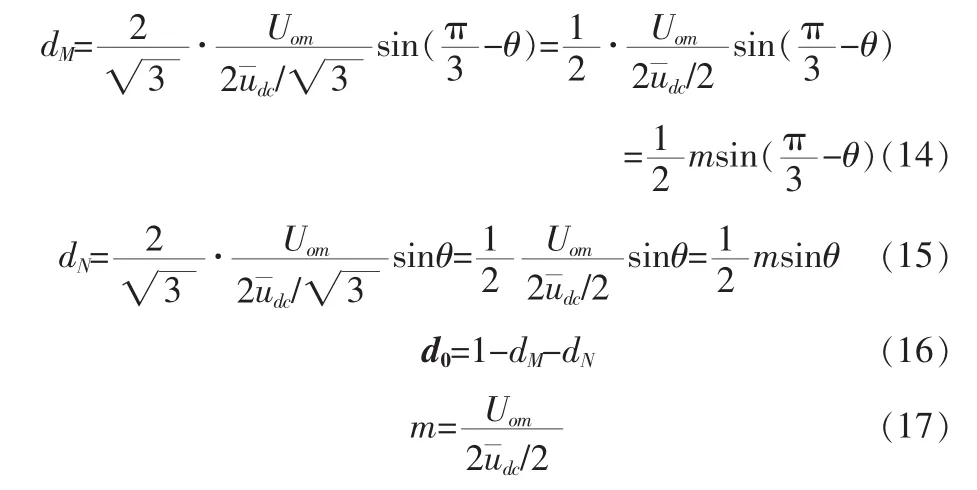
其中，d0为零电压矢量，Uom为输出线电压空间矢量US的幅值，m为逆变级的调制比。

因为在实际情况中，u¯dc是变化的，所以实际的调制比为（将式（13）代入式（17））：

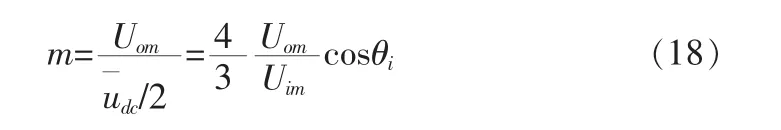
由于整流级的一个调制周期内两个时间段内的直流电压是不同的，所以逆变级的调制周期也要分为两个阶段进行。为了保证系统的电压传输比，应使一个调制周期内的输出矢量相位相同，所以整流级和逆变级的两个时间段的占空比应该相同：

第一段时间TAB：

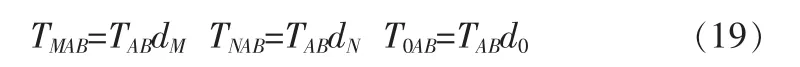
第二段时间：

所以在TAB时间段内，矢量UM分配的时间为TMAB，UN分配的时间为TNAB，U0分配的时间为T0AB；在TAC时间段内，矢量UM分配的时间为TMAC，UN分配的时间为TNAC，U0分配的时间为T0AC。

4 TSMC的换流

TSMC相对传统矩阵变换器来说，无需复杂的四步换流，换流简单可靠。逆变级开关的换流可直接采用传统的直—交逆变器的可靠地换流方法。

整流级双向开关的换流，当双向开关换流是逆变级都工作在零电压空间矢量状态，这样就可以实现整流级的零电流环流，简单可靠，这也是TSMC最主要的优点之一。

5 仿真分析

图4 直流电流和直流电压仿真波形Fig.4 Simulation waveform of DC current and DC voltage

本文基于Matlab∕Simulink建立了TSMC的仿真模型，仿真参数如下：输入相电压为380 V，三相对称阻感负载为电阻R=1 Ω、电感L=5 mH，系统的调制频率为6 kHz。由于直驱式风力发电系统中永磁同步发电机发出的为频率变化的交流电，然后通过TSMC变为与电网同频率的交流电。所以系统仿真主要验证在输入电压频率变化的情况下，系统能否较好的输出与电网频率相同的交流电。

第一种情况当输入电压为50 Hz时，输出电压也为50 Hz。系统的仿真结果如下，图 4（a）为直流电流波形，图 4（b）为直流电压波形，由图可知直流电压主要在输入线电压的幅值和其三分之一间变动，并且始终保持为正。图5为输出电压和电流波形。图6为输出电流的频谱分析。

图5 输出线电压和电流仿真波形Fig.5 Simulation waveform of output line voltage and current

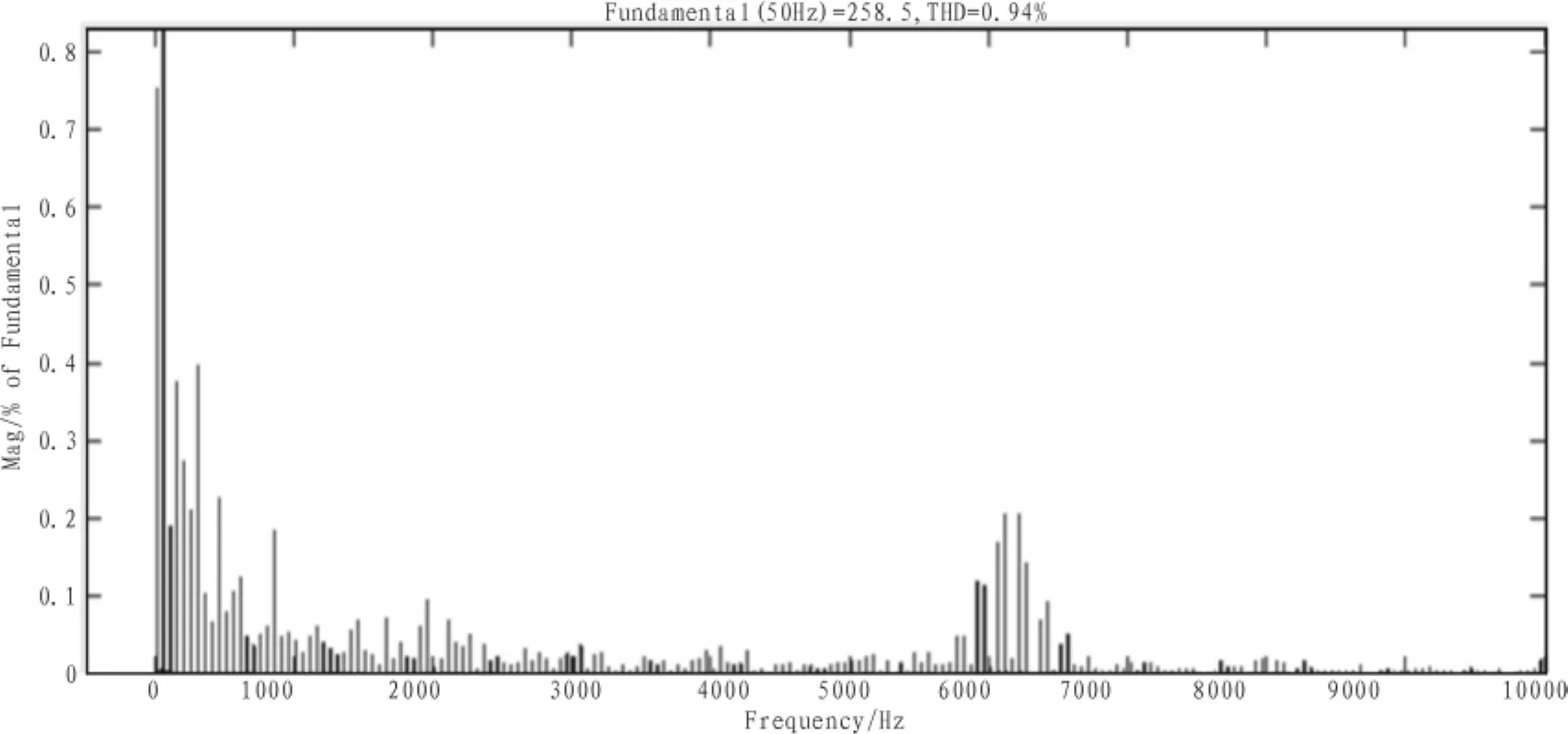
图6 输出电流的频谱分析Fig.6 Spectral analysis of the output current

第二种情况输入电压为100 Hz，输出电压为50 Hz时，系统的仿真结果如图7所示。图7（a）为输出电压波形，（b）为输出电流波形。

第三种情况输入电压为30 Hz，输出电压为50 Hz时，系统的仿真结果如图8所示。图8（a）为输出电压波形，（b）为输出电流波形。

根据仿真结果可得：TSMC在不同输入频率的情况下，都能有稳定的输出50 Hz的交流电压，很好的满足直驱式永磁风力发电[7]系统对全功率变换器的要求，并且通过FFT分析可以了解到，系统除了开关频率附近的高频谐波，其他低频谐波的分量很小，所以通过仿真结果可以得出TSMC具有优秀的输入输出性能，并且非常适用于直驱式永磁同步风力发电系统。

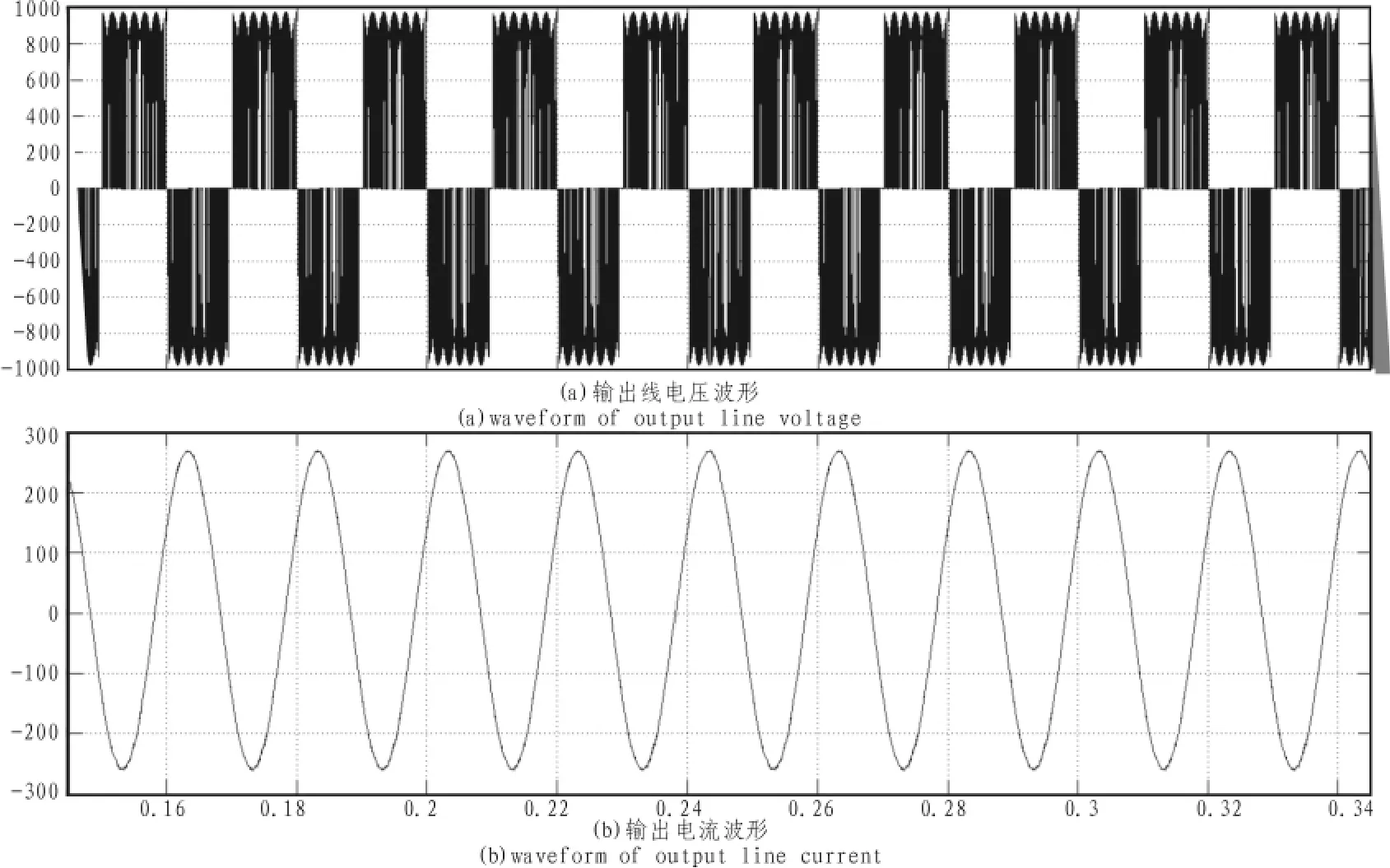
图7 输入电压为100 Hz时输出电压和电流波形Fig.7 When the frequency of input voltage is 100 Hz，the output voltage and current waveforms

图8 输入电压为30 Hz时输出电压和电流波形Fig.8 When the frequency of input voltage is 30 Hz，the output voltage and current waveforms

6 结束语

本文首先分析了直驱式风力发电系统的优势以及对全功率变流器的要求，在此基础上研究了将TSMC作为直驱式风力发电系的全功率变流器，充分发挥了TSMC的各项优势，是直驱式风力发电系统的性能优势更加突出。然后对TSMC整流级的PWM调制和逆变级的空间矢量调制进行了计算和推导，并且分析了TSMC的换流方法。最后通过MATLAB对整流级和逆变级的调制策略进行了仿真验证，并且对不同频率输入的情况下的TSMC的稳定输出能力进行了验证。同时也为以后的研究提供了理论基础。

[1]李建林，许洪华.风力发电中的电力电子变流技术[M].北京：机械工业出版社，2008.

[2]瞿兴鸿，廖勇，姚俊，等.永磁同步直驱风力发电系统的并网变流器设计[J].电力电子技术，2008，42（3）：22-24.

QU Xing-hong，LIAO Yong，YAO Jun，et al.Design of gridconnected converter for a permanent magnet synchronous direct-drive wind powergeneration system [J].Power Electronics，2008，42（3）：22-24.

[3]孙凯，周大宁，梅杨.矩阵变换器技术及其应用[M].北京：机械工业出版社，2007.

[4]邓文浪，杨欣荣，朱建林，等.18开关双级矩阵变换器的空间矢量调制策略及其仿真研究 [J].中国电机工程学报，2005，25（15）：84-90.

DENG Wen-lang，YANG Xin-rong，ZHU Jian-lin，et al.Space vector modulation strategy of two-siage matrix converter with 18 Switches and It’s Simulation Study[J].Proceedings of the CSEE，2005，25（15）：84-90.

[5]刘见，粟梅，孙尧，等.基于双级矩阵变换器的永磁同步电机矢量控制[J].电力电子技术，2010，44（11）：65-68.

LIU Jian，SU Mei，SUN Yao，et al.Permanent magnet synchronous motor vector control based on Two-stage matrix converter[J].Power Electronics，2010，44（11）：65-68.

[6]王汝田，王建元，王永，彭茂君.双级矩阵变换器的简化调制方法[J].高电压技术，2010，36（7）：1815-1820.

WANGRu-tian，WANGJian-yuan，WANGYong，etal.Simplified modulation method for two-stage matrix converter[J].High Voltage Engineering，2010，36（7）：1815-1820.

[7]邹园，盛四清，虢韬.基于HHT风力发电系统谐波检测方法的研究 [J].陕西电力，2011（12）：54-57.

ZOU Yuan,SHENG Si-qing,GUO Tao.HHT-based wind power system harmonic detection[J].Shaanxi Electric Power,2011（12）：54-57.