基于GARCH模型VAR方法的人民币外汇交易风险控制

姬会英

0 引言

2005年7月21日，我国开始实行以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度。人民币自汇率改革以来成绩明显，在国际收支平衡、扩大内需、调整结构上都发挥了积极作用。2010年6月份以来，全球经济逐步复苏，我国经济回升向好的基础进一步巩固，经国务院批准，人民银行决定进一步推进人民币汇率形成机制改革，增强人民币汇率弹性。从2005年汇率改革实施到现在，人民币已经升值了23.6%，汇率的波动会对我国的进出口贸易产生重大影响，人民币的持续升值预期会不断吸引外国的投资和热钱的流入，但是不良的资本流动，有可能造成金融动荡。在汇率形成机制的变革上，这不仅意味着那些与国际贸易和国际金融业务联系紧密的金融机构和企业将要面临更多汇率风险，也促使那些与国际贸易关联不大的企业与公众增强汇率风险意识。

本文分析了2005年6月以来人民币/美元的波动情况，采用最近几年比较流行的风险度量和分析工具——基于GARCH模型的Var方法，GARCH模型能够很好的消除序列的相关性和异方差性，而Var方法在测度范围和精度上都比其他工具具有优势，希望能够比较准确的拟合和量化汇率的波动风险，为金融监管机构以及外汇投资者提供一个比较完善的技术解决方案和一定的理论参考。

1 研究方法

1.1 GARCH模型

在现实中，市场收益率并不服从标准的正态分布，而是表现出尖峰后尾并且波动集聚的特征。为了处理波动集聚和收益率的后尾特征，Engle在1982年依据残差项εt的条件方差依赖于它的前期值εt-1的大小，提出了自回归条件异方差（ARCH）模型，假定 εt在给定（t-1）时间内和信息 Ωt-1的情况下满足正态分布，即 εt—Ωt-1～（0，δ2），则其条件方差为。 其 中 α0，α1...αq＞0,且时，ARCH（q）是稳定过程。

然而在实际应用中，为了达到更好的拟合效果，常常需要更大的误差项滞后阶数，这样不仅增加待估参数的个数，而且还会降低参数估计的效率。针对这个问题，Bollerslev在1986年扩展了Engle的模型，引入了一种允许条件方差转化为一个ARMA过程的方法。即广义自回归条件异方差（GARCH）模型。表达式为：δ2t=α0+，其中：p≥0,q≥0, α0＞0，αi≥0(i=1,2,…,q), βi≥ 0（i=1,2,…，p），保证GARCH模型的平稳性，必须满足

ARCH（q）模型是最常用的波动建模工具，在金融时间序列的预测中有着广泛的应用，其中又因低阶的GARCH（p，q）模型拟合效果较好，在现实应用中被普遍应用到金融时序的拟合预测中去。

1.2 Var测算方法

Var是一种利用统计技术来度量有价证券金融市场风险的方法，是指在正常的市场波动条件下，资产组合在给定置信度和一定持有期内可能的最大损失。表达形式为：Prob(△W(△x，△t)≤-VAR)=1-c。其中，△W表示投资组合持有期△t的变化量，c为置信水平，Var即为在置信水平c下处于风险暴露中的头寸。

Var值有绝对值和相对值两种表示方式，绝对值Var可以表示为:绝对值Var=-W0[z(a)δ Δt-u]；相对Var值可以表示为：相对值Var=-W0z(a)δ Δt。其中W0为投资组合初始价值,u为收益率的期望值，z(a)为置信度为a的对应分布函数的临界值，△t为持有期。如果期限较短，这两种方法都将给出近似的结果。相对Var值在实际运用中更为广泛，因此本文选则相对Var值来计算损失。这种方法把所有的不确定性都体现在δ上，其他的分布会得到不同的δ值。

综合上述关于GARCH模型和Var风险测算方法的介绍得出基于GARCH模型的Var计算公式为：Var=-W0z(a)，其中。W0为初始时刻投资组合的价值，z(a)为置信度为a的对应分布函数的临界值，△t为持有期。

2 实证分析

2.1 样本选取

本文选取2005年6月3日到2011年3月18日的美元兑人民币的中间价日汇率数据，共863个，所有数据来源于国家外汇管理局提供的统计数据。应用Eviews5.0进行数据处理，并进行相应的分析和处理。

2.2 数据处理

用Pt表示美元兑人民币日汇率t期中间价，rt表示收益率，为了缓解收益率序列的波动幅度，采用对数差分的方法，用公式表示为，rt=ln Pt/Pt-1。采用连续收益率法计算日收益率，用Eviews5.0软件对数据进行初步统计分别得出日收益率波动曲线直方图及相关描述统计量，如图1所示。

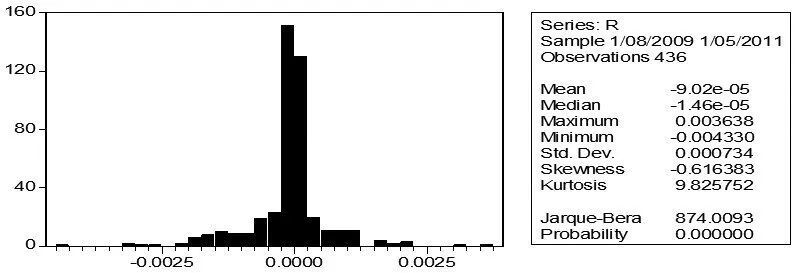
图1 美元/人民币日收益率的直方图和相关统计量

由图1可知，样本期内，日收益率序列偏度S=-0.6164，峰度为K=9.8258，与标准正态分布（S=0,K=3）相比，呈现出左偏、尖峰的特征。Jarque-Bera的正态性检验为874.0，p值为0，充分说明日收益率分布显著异于正态分布，并从图1中看出其收益分布呈现“厚尾”特征。又由下图2可以看到，收益率的波动呈现明显的集聚性特征。

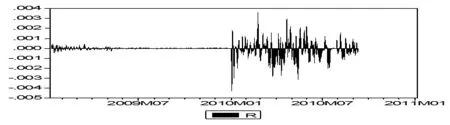
图2 美元/人民币日收益率波动图

对收益率序列进行单位根检验，滞后阶数选择为12，包含常数项。检验结果显示，ADF=-17.647，其小于在1%显著性水平下的临界值-3.4452，因此本样本时间序列不存在单位根，这表明人民币/美元日收益率序列是平稳序列。

对收益率序列进行序列相关性检验。在滞后阶数为12的相关图上看，日收益率序列的自相关函数和偏自相关函数值都很小，均小于0.1，并且趋于0，表明收益率序列并不具有自相关性。Ljung-Box-Pierce Q检验的结果也说明日收益率序列不存在明显的序列相关性。因此，本文不妨设日收益率方程为：rt=c+εt。

由上分析，我们可以看出，人民币/美元的收益率分布并不服从标准的正态分布，而是表现出尖峰、厚尾的特征，并且波动呈现集聚性。

2.3 建立模型

首先通过ARCH LM检验来判断美元/人民币收益率序列是否存在ARCH效应。本文选择滞后12阶的LM统计量(Obs*R-squared)值的相伴概率为0.00，小于0.05的显著性水平。因此，拒绝原假设，残差序列存在高阶ARCH效应，故选择GARCH模型。

采用赤池信息准则（AIC）和施瓦茨（Schwarz）贝叶斯信息准则（SBIC）判别模型阶数，使所选定的阶数能够使信息准则的数值达到最小。本文经过比较GARCH（1，1）、GARCH（1,2）、GARCH（2,1）和GARCH（2,2）产生的AIC和SBIC的大小，得出模型选择GARCH（1,1）时，对应的AIC和SBIC值最小，基于此，本文最终选择GARCH（1，1）模型来计算δ值。

2.4 基于GARCH（1,1）模型的预测

运用Eviews软件最终拟合的GARCH（1,1）模型见表1。

表1 人民币/美元日收益率GARCH（1,1）模型拟合结果

由α1+β1=0.9905＜1得出拟合好的GARCH模型是平稳的。

对拟合的GARCH（1，1）模型再次进行ARCH LM检验残差是否已经消除了ARCH效应。选择滞后10阶的LM统计量(Obs’R—squared)值为0.157，小于0.05置信水平的临界值18.307，且对应P值为1.00，表明经过GARCH(1，1)模型处理残差序列已不存在ARCH效应。

本文由GARCH（1,1）对人民币/美元汇率估计模型进行预测，得到均方差误差为0.000736.从预测图上得出RMSE、MPE和Theil系数均较小，说明模型拟合效果较好，预测准确度高。对人民币/美元进行样本外预测，得出2011年3月21日的中间价汇率为6.5578.而真实汇率为6.5632，预测误差为0.067%，进一步说明模型预测精度好。

2.5 基于GARCH（1,1）模型的Var值计算

由GARCH（1,1）模型得到δ为0.0036。从事人民币/美元交易者就可以由公式Var=-W0z(a)δ Δt得出△t时期内可承受的外汇波动损失。假如交易者拥有100万，a选取为5%，△t为1天，那么外汇波动损失Var值为0.594万。

综合上述分析，可以得出GARCH（1,1）模型能够很好的拟合金融危机以来人民币/美元的日收益波动分布特征，且消除了异方差性和序列相关性造成的影响，能够为我国监管部门和进出口企业基于Var外汇风险测算方法进行风险控制提供更接近实际情况的值，为他们进行正确的分析和决策提供了技术支持。

3 结论

本文通过对2005年6月3日到2011年3月18日的人民币/美元日中间价汇率进行分析，得出这段时期人民币持续升值，人民币和美元之间的比率不断变大。本文实证分析得出GARCH（1,1）模型能够很好的拟合日收益率序列的分布，从而能够更好的反映外汇汇率日波动性，进而能够更准确的计算出VAR方法中代表波动性的δ值。为我国进出口企业基于VAR方法进行外汇风险控制提高了正确率，具有重要的参考价值。

因此，随着人民币和美元的比率波动不断变大的趋势，我国进出口企业应从以下几个方面来控制和规避风险：

（1）预测未来汇率变动趋势。

预测未来外汇汇率变动的趋势，是每个进出口企业在浮动汇率制度下最重要的一项研究工作，也是做好其他避险工作的关键。但由于影响汇率变动的因素很多，不只是受到有关货币当局经济力量及政治状况的影响，有时甚至连某国政府的一个临时措施也足以影响汇率的变动。因此，预测未来汇率变动的趋势也是企业在实际工作中最难把握的学问。尽管如此，在当前国际金融市场动荡不定的情况下，每个进出口企业仍要积极创造条件把这项工作做好。

（2）积极利用金融衍生工具。

从国际范围看，衍生金融工具已经发展成为最主要的交易风险管理手段，目前在金融市场上进行交易的衍生金融工具品种已经超过3 000种，而其中最重要的金融衍生工具主要有远期外汇交易与外汇期货交易，进出口企业有效合理的运用金融衍生工具对于风险的防范极为重要。

（3）合理选择合同货币。

随着人民币在周边国家和地区的币信逐步提高，特别是伴随香港人民币离岸业务的开展，人民币在通往自由兑换的道路上稳步前进，进出口企业在进出口贸易中应不失时机地加强人民币计价结算的比重。但是在选择合同货币时还必须注重“收硬付软”的原则，即出口、借贷资本输出争取使用硬币，进口、借贷资本输入争取使用软币。这一原则的困难在于，由于“硬”、“软”并不是绝对的，企业管理人员难以掌握其变化规律，因此企业可以与银行建立联系，在专业人员的帮助下对汇率走势做出正确的判断。

（4）要灵活掌握收付时间。

进出口企业应根据实际情况灵活掌握收付时间。如果作为出口企业，当计价货币呈上升趋势时，由于收款日期越向后推就越能收到汇率收益，故企业应在合同规定的履约期限内尽可能推迟出运货物，或向外方提供信用，以延长出口汇票期限。当然，这要在双方协商同意的基础上才能进行。

但必须认识到，企业管理汇率风险的过程是复杂的，应把风险管理与其整体经营和发展战略融合起来，确保企业拥有一个长期性的汇率风险管理策略。对于目前的中国企业来说，最为重要的是要树立汇率风险意识，将汇率风险的思想融入到企业的经营管理之中，形成一整套汇率风险管理机制，对于不具备建立自己汇控部门的广大中小型进出口企业，可以通过与银行建立长期合作关系，利用银行提供的专业金融工具，实现汇率风险控制，为企业长期健康稳定和持续地发展创造条件。

总之，人民币汇率的趋势和幅度的不确定性，使得汇率风险成为进出口企业的一种经常性的、不可低估的风险。对于企业在外汇风险防范的具体措施，企业可以利用基于GARCH模型的VAR方法在大概明确外汇汇率变动的基本趋势的基础上，结合企业本身具体情况，灵活选择可行的工具进行相应短、中、长期外汇风险管理。

[1]Bollerslev Tim.Generalized Autoregressive Conditional Het-Eroske⁃dasticity[J].Journal of Econometrics,1986,(31).

[2]Engle R.F.Autoregressive Conditional Heteroskedasticity with Esti⁃matesof the Varianceof U.K[J].Inflation Econometrica,1982,(50).

[3]Javiera Aguilar,Stefan Nydah.l Central Bank Intervention and Ex⁃change Rates:the Case of Sweden[J].Journal of International Finan⁃cial Markets,Institutions and Money,2000,(10).

[4]Torben G.A.,Tim Bollerslev,Francis X.D.,PaulLabys.The Distribu⁃tion of Realized Exchange Rate Volatility[J].Journal of American Sta⁃tistical Association,2001,96(453).

[5]王德全.外汇风险度量研究[J].南方金融，2009，（5）.

[6]翟爱梅.基于GARCH模型对人民币汇率波动的实证分析[J].技术经济及管理研究，2010，（2）.

[7]闫海峰.基于GARCH-M模型的人民币汇率预测[J].重庆工商大学学报（社会科学版），2009，（8）.

[8]魏金明.VaR模型在人民币汇率风险度量中的应用[J].上海商学院学报，2009，（7）.

[9]刘瑾，施建淮.基于ARCH类模型的VaR方法在外汇风险计量中的应用[J].国际金融研究，2008，（8）.

[10]Philippe Jorion.风险价值VAR[M].上海：中信出版社，2005.