基于支持向量机的关键因素拟合指数化投资方法

倪丽云,沈传河,王向荣

0 引言

积极指数化投资（Active Indexing Portfolio）作为全新的投资模式，其主要表现形式之一为“积极”的指数组合管理（陈春峰、陈伟忠，2004）[1]，包括如何复制指数这个最主要环节，并要求确定精选成分股和选择有利于平衡组合、产生超额回报的赋权方式。这种投资方法的实质是通过采取科学的选股和赋权方式，在控制跟踪误差的基础上实现预期的超额收益。

本文将在积极指数化投资模式框架下，建立基于支持向量机的双目标指数跟踪模型，实现在控制跟踪误差的基础上，寻求预期的超额收益，实现投资收益最大化。具体思路是：首先借鉴Francesco Corielli与Massimiliano Marcellino（2002）提出的基于因素的指数跟踪方法以及张鹏、瞿宝忠（2004）使用的关键因素拟合方法，对拟构建投资组合进行前期的成分股票选择[2-3]。然后，在满足投资约束条件下，利用支持向量机完成成分股票的权重优化，求出投资组合的资金分配系数。最后，根据选定的度量指标，在测试数据环境下分析投资组合的效果。

1 目标指数的关键因素拟合方法

指数跟踪要求构建一个证券投资组合，使得它的变化行为尽可能地接近给定的目标指数。一般情况下，这个投资组合中的证券数目应该比目标指数少，并且在跟踪误差中也不应该含有较低频率（即较差持续性）的成分，这意味着正常误差应该源自于投资组合中主要的或是关键性的影响因素，进而才能保证这个复制的投资组合很好地适应或捕捉目标指数未来的变化，包括收益率和波动性。

正因如此，Francesco Corielli和Massimiliano Marcellino（2002）和张鹏、瞿宝忠（2004）先后提出基于因素或关键因素拟合的指数化投资策略，以力图解决这个问题[2－3]。这种方法需要两步来完成，即构建与目标指数具有同样可持续性（也即高频率）因素组成的复制组合，然后再尽可能地使跟踪误差减少到最小。

首先，找出影响目标指数走势的关键性因素。

设设It、Pit分别为目标指数和第i只股票在时刻t的价格，Rt、rit分别为它们在第 t个周期内的相对收益率，则有:

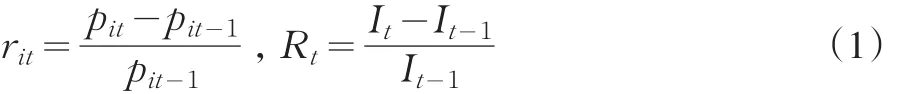
相应地，投资组合在第t个周期内的相对收益率R't则为：，其中n为投资组合待定成分股票的数量，wit为第i只股票在时刻t的权重。

根据目标指数成份股个股的日收益率为基础进行因子分析，提取出反映目标指数走势的m个共同因子，这m个共同因子即代表了影响目标指数走势的m个关键因素。在此基础上，构造以下的多因素模型:

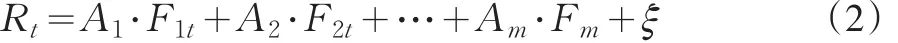
式中Fmt为第m个共同因子Fm在时刻t的值，Am为这个共同因子对目标指数的贡献率，ξ为残差。

在找出这m个关键因素之后，需进一步找出这m种关键性的共同因子所代表的样本股。它们对应的关系如下:

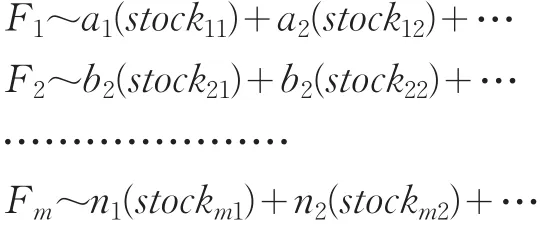
其中stock为共同因子所代表的样本股；a、b、…、m为样本股对共同因子的贡献率，即因子负荷。

观察共同因子的因子负荷强弱，据此可以分析判断出各个共同因子所反映的关键因素，并对它们进行相应的解释。

其次，需验证挖掘出的这m个关键因素是否真的能够反映目标指数的走势。现在，可用它们中最具代表性的一组样本股构造出一个投资组合，与目标指数进行比较，验证是否投资组合与目标指数等价。

为此，找出这m个关键因素最有代表性的n个样本股，按照其方差对总方差解释的贡献率所占比重作为权重构造投资组合如下：

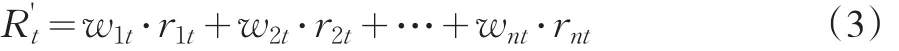
计算出投资组合的日收益率和目标指数的日收益率，在通过相关性检验之后，将它们进行线性回归分析。构造以下回归模型：

式中b为常数项，a为回归系数，ξ为残差。

如果该模型经检验成立，并且b趋近于0，同时a趋近于1，那么R't≈Rt，即投资组合与目标指数等价，说明找出的这m个关键性因素能够真实地反映目标指数的走势，投资组合可以代替目标指数进行指数化投资。

以上方法可以通过主成分分析法(Principal Components Analysis)来实现。但这种方法会不可避免地损失一些有价值的信息，而且各因素对应的样本股选择及其权重确定在一定程度上存在主观性，势必增大投资组合的跟踪误差，影响指数化投资的效果。为克服这种情况，下面将采用支持向量机对（3）式拟选定的成分股进行权重优化，而不仅仅根据它们的因子负荷（即方差贡献）来确定。

2 基于支持向量机的关键因素拟合方法的实现途径

2.1 支持向量机算法

支持向量机SVM(Support Vector Machines)是Vapnik等人建立的一种新的机器学习方法[4]。它是在以解决有限样本机器学习问题为目标的统计学习理论(Statistic Learning Theory，SLT)基础上发展起来的。SVM建立在SLT的VC维理论和结构风险最小化（SRM）原理的基础上，根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误地识别任意样本的能力)之间寻找最佳折衷，以期获得最好的推广能力。它通过使用结构风险最小化（SRM）代替传统的经验风险最小化（ERM），使用满足Mercer条件的核函数，把输入空间的数据变换到一高维的Hilbert空间，训练的复杂度与输入空间的维数无关，只与训练的样本数目有关。因此，SVM能够有效地避免经典学习方法中出现的过学习、欠学习、“维数灾难”以及陷入局部极小点等诸多问题，因而在解决小样本、非线性及高维模式识别问题中表现出很多独特的优势。在这里，将分析普通的、采用ε-不敏感函数的支持向量回归机ε-SVR。

给定训练集{ }xi,yi，i=1,2,…,l，其中输入数据x是一个欧式空间Rn，y∈R，是实数R的封闭子集。借助特定的非线性映射φ(x)，输入x被映射到高维空间(或称特征空间)。函数逼近问题，就是在像空间上通过机器学习能够选择一个特定的函数：

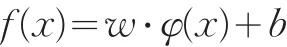
根据推广理论，要解出决策函数 f(x)，可考虑经过适当定义的核函数 K(⋅,⋅)：

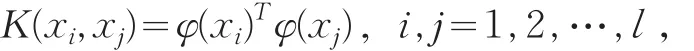
引入ε-不敏感损失函数，即：

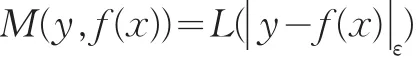
式中：

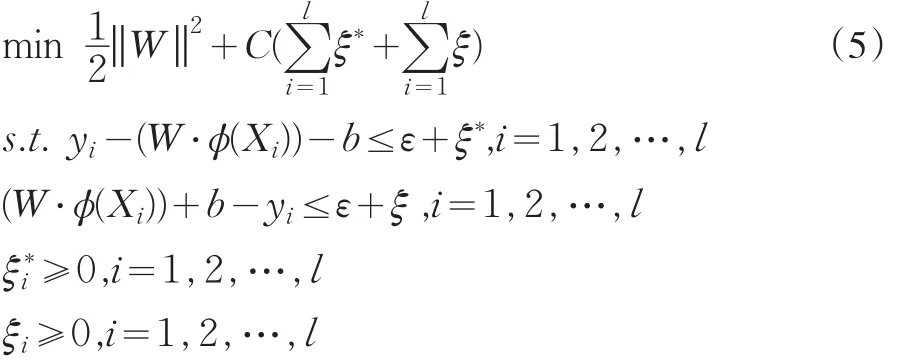
其对偶问题为：

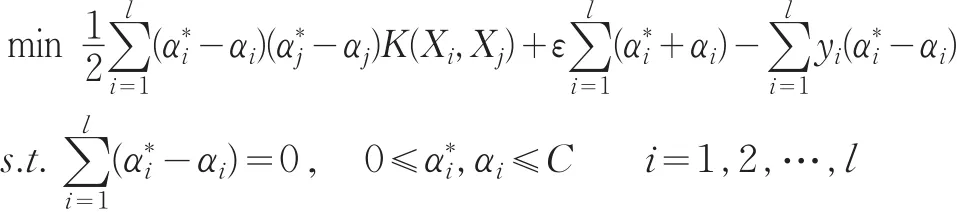
解上式，得到：

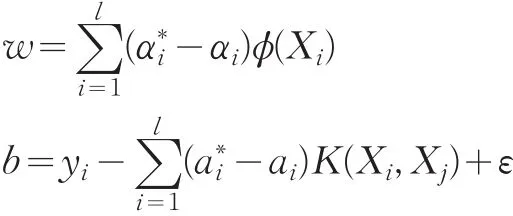
因此：

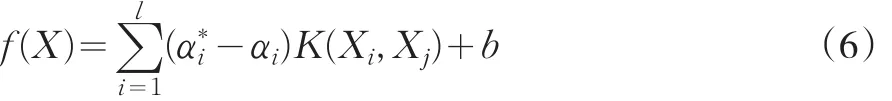
任何满足Mercer条件的对称函数都可以成为核函数，并可建立不同的学习模型[5]。目前最常使用的核函数为多项式核函数：

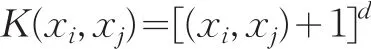
径向基核函数(RBF)

Sigmoid核函数：

其中u＞0,v＜0，并且，任何核函数的非负线性组合仍然是一个Mercer核。一旦核函数确定后，参数γ和σ2（sig2）就可以进一步优化出来。

现在，利用测试集来检验这个模型。模型的预测精度用标准均方差（the normalized mean squared error，NMSE)和平均绝对差（the mean absolute error，MAE)等统计标准来测度，其定义如下：

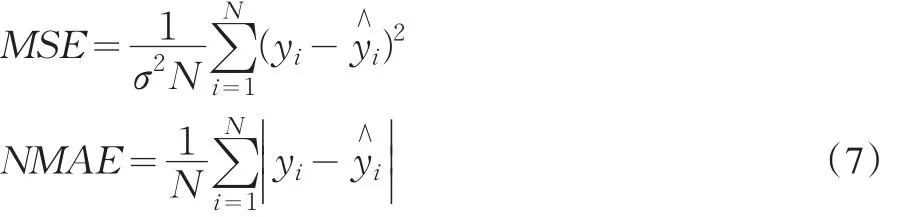
其中，σ2是数据的标准方差。

2.2 支持向量机框架下的关键因素拟合模型

利用支持向量机构建投资组合的主要任务是对（3）式中的权重Wit进行优化。考虑到Wit与时间有关，直接求解将非常困难，可采取固定比例策略，即Wit变为Wi。这意味着在任何周期内，投资组合成分股票各自权重将保持不变，并存在一定优势(张鹏、瞿宝忠，2004）[2-3]。

在ωi给定为固定比例的前提下，参考（3）式，则第t个周期内的投资组合与目标指数收益之间的跟踪误差et满足:

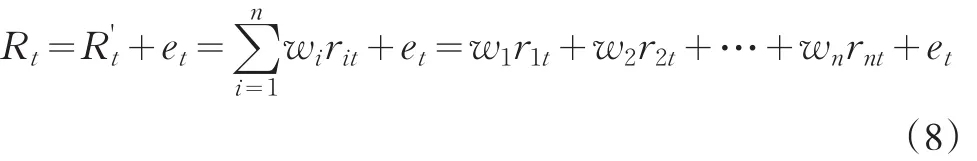
所以，确定投资组合的权重wi可以看成是在训练集{ }xi,yi上对（8）式进行多元线性回归。在这里，xt=Rˉt=(r1t,r2t,…,rnt)'，yt=Rt。

这时，需考虑（5）式中约束条件的变化。在投资组合构建中，应考虑资本预算约束、成分股票投资比例限制、整数约束、交易成本及管理费用约束等。设投资组合成分股票i最小比例为ηi、最大比例为δi。相应地，（4）式应变为:

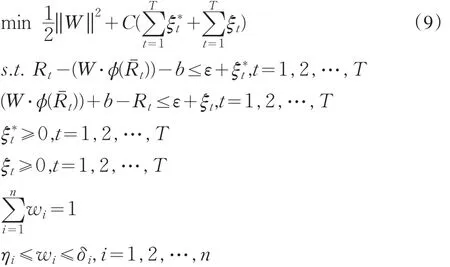
解（9）式，即可得到形如（6）式的回归函数，其中的系数即为欲求的权重。

3 实证分析

以“上证50”指数（000016）为例，数据取自清华金融研究数据库（THFD）。时间为2008、2009两年内的市场交易数据，具体为2008年7月1日至2009年12月31日，扣除休盘时间，计得370个指数的日收盘价格。同时，得到该指数50个成分股票在上述时间期限内的各自370个日收盘价格。然后根据（1）式可计算得到指数及其成分股票各自对应的369个日收益率。

将上述370个日收益率数据分成两部分，即2008年7月1日至2009年9月30日和2009年10月9日至2009年12月31日，分别对应309个和60个数据用于训练和测试。

3.1 利用关键因数拟合技术构建投资组合

利用Eviews 5.0软件进行主成分分析。首先，对各样本股日收益率数据采用KMO统计量和Bartlett’s球形检验，以判断样本数据是否符合因子分析的前提条件。其次，采用正交旋转，具体旋转方法为方差最大化正交旋转(Varimax)。根据提取的主成分共同因子的累积贡献率达到约85%以上为标准，一共提取19个共同因子、20个共同因子代表样本股，其结果显示在表1中。

3.2 利用支持向量机进行训练和测试

在（9）式中，考虑到我国基金管理办法规定，取δi≤10%；尽管融资融券业务正在展开，但由于涉及到的股票品种少，“上证50”指数成分股票并没有全部惠及，所以在这里还是规定wi＞0，强调不允许卖空交易；进而存在ηi＞0，即不允许剔除出投资组合，主要因为作为投资组合的成分股票，已经过关键因素拟合方法选择，它们本身已代表了目标指数收益和波动中的不同影响因数。

通过MATALAB 7.0软件运行，先根据（9）式对常规支持向量回归机ε-SVR的程序进行调整，以充分反映投资组合的约束条件。然后，采用径向基核函数(RBF)，参数ε、c和σ2(sig2)分别置为。求得的权重系数详见表1：

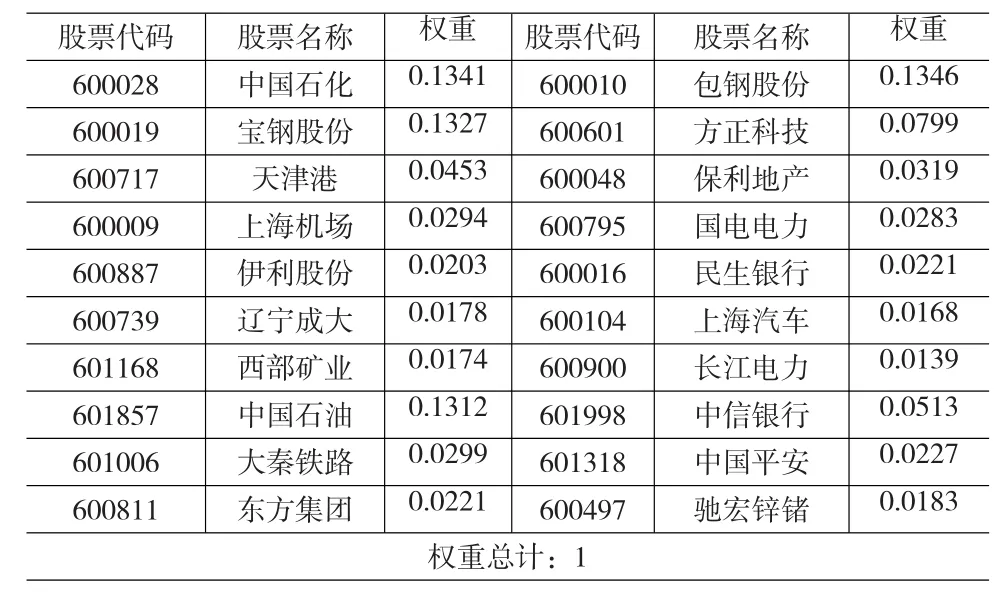
表1 投资组合成分股列表

3.3 效果分析

利用Sharp指数和信息比率（Information Ratio，IR）两个指标来衡量投资组合的效果，考察其积极化程度。同时，又与完全复制方法相比较，进一步分析基于支持向量机的关键因数拟合指数化投资方法的特性。

在Grinold和Kahn(2005)关于积极组合管理的讨论中，信息比率被视为积极组合管理的关键，它用跟踪误差来衡量投资组合的风险水平，考察了投资组合在特定的跟踪误差下实现超额收益的能力。通常，信息比率大于0.5被认为是较好的水平；而纯粹指数投资的信息比率为0[6]。而Sharp指数则同时考虑了包括系统风险和非系统风险在内的总风险，侧重于投资组合在分散和降低非系统风险的能力，反映了投资组合的内在质量。具体结果见表2，其中的跟踪误差依据（8）式计算得出。

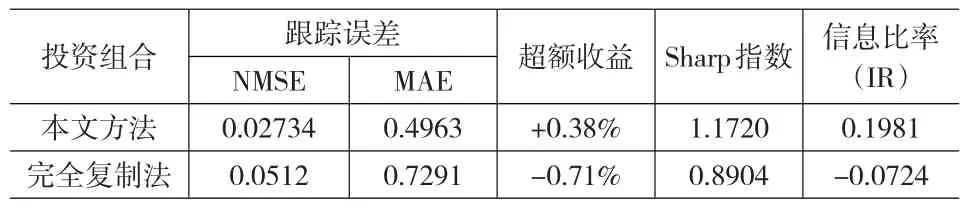
表2 模型的效果测试

可以看出，本文建立的基于支持向量机的投资组合权重确定方法达到了较好的效果，对目标指数的跟踪误差无论是NMSE值还是MAE值，都比较小，并优于完全复制方法。而且，Sharp指数和信息比率IR也都高于完全复制方法，也因此取得了0.38%的平均超额收益。

4 实证分析

本文利用基于结构风险最小化原则的支持向量机进行指数化投资组合的构建，提高了投资组合的样本外跟踪效果，有效解决了现有指数化投资组合方法由于使用经验最小化原则而带来的不足，克服了过度依赖样本进行跟踪误差分析的局限。而且基于关键因素拟合方法的投资组合成分股票的前期选择，能够有效捕捉目标指数波动中的高频因数，增强了投资组合把握目标指数动态特性的能力。因此，上述两种方法的集成无疑克服了各自的缺点，而由此形成的优化复制目标指数的途径将不啻是一种有效的尝试。正如实证分析所示，这种方法在模型鲁棒性和指数跟踪误差方面都具有良好的表现。进一步的研究方向应集中在双目标函数上，即在控制跟踪误差基础上，实现超额收益最大化。并且，改进投资组合成分股票的前期选择方法，相应调整常规支持向量机程序，优化算法设计，提高数据挖掘性能。

[1]陈春峰,陈伟忠.积极指数化:一种全新的投资模式[J].证券市场导报，2004，（11）.

[2]Francesco Corielli,Massimiliano Marcellino.Factor Based Index Tracking[J].Centrefor Economic Policy Research,2002，（3）.

[3]张鹏,瞿宝忠.关键因素拟合指数化投资方法的实证研究[J].证券市场导报，2004，（11）.

[4]Vapnik V N.The Nature of Statistical Learning Theory[M].New York:Springer-Verlag,1995.

[5]Wahba G.Support Vector Machines,Reproducing Kernel Hilbert Spaces,and Randomized GACV.Advances in Kernel Methods-Sup⁃port Vector Learning[M].Cambridge:The MITPress,1999.

[6]Richard C.Grinold,Ronald N.Kahn.Active Portfolio Management:A Quantitative Approach for Providing Superior Returns and Controlling Risk[M].New York：McGraw-Hill,2000.