基于特殊准随机结构模型的FCC Fe-Cu无序固溶体合金的弹性稳定性
2012-09-26温玉锋
温玉锋,孙 坚,黄 健
(上海交通大学 材料科学与工程学院,上海 200240)
基于特殊准随机结构模型的FCC Fe-Cu无序固溶体合金的弹性稳定性
温玉锋,孙 坚,黄 健
(上海交通大学 材料科学与工程学院,上海 200240)
采用基于投影缀加波赝势和广义梯度近似的第一性原理计算方法计算FCC 结构Fe以及3种Fe-Cu无序固溶体合金(Cu原子摩尔分数分别为25%、37.5%和50%)的基态性质、弹性常数以及电子结构,其中Fe-Cu无序固溶体合金采用特殊准随机结构模型进行计算。能量计算结果表明:FCC结构Fe存在无磁、低铁磁以及高铁磁性3种状态,而FCC 结构Fe-Cu无序固溶体合金只存在无磁与高铁磁性两种状态。高铁磁性FCC 结构Fe不满足Born弹性稳定性准则,铁磁性FCC 结构Fe-Cu无序固溶体合金的弹性稳定性随着Cu 含量的增加而增加;当Cu 原子的摩尔分数不低于37.5%时,Fe-Cu无序固溶体合金满足Born弹性稳定性准则,此时合金以亚稳态形式存在。
Fe-Cu无序固溶体合金;特殊准随机结构;弹性性质;第一性原理
热力学平衡相图中Fe-Cu系两组元互溶度很低,且相互间不形成任何金属间化合物,合金的组织通常为两个端际固溶体的混合物。然而,采用液态淬火、气相淬火以及机械合金化等方法可以显著提高Fe-Cu固溶体的固溶度,制备出各种组成的亚稳态Fe-Cu固溶体合金。例如,采用机械合金化方法可以使体心立方(BCC)结构Fe-Cu合金中Cu原子的摩尔分数增加到约10%,面心立方(FCC)结构Fe-Cu合金中Cu原子的摩尔分数也可降低到约30%[1]。另一方面,含Cu的铁素体钢或奥氏体钢时效后会析出富Cu第二相,并对铁素体钢或奥氏体钢产生析出强化效应。关于铁素体钢中富Cu析出相的晶体结构一般认为是析出初期为BCC结构,随着析出相中Cu含量的增加转变为9R结构,并最终转变为FCC晶体结构[2]。然而,各阶段不同晶体结构的析出相中Cu含量还存在很大的争议。GONG 等[3]利用分子动力学与第一性原理方法计算了BCC与FCC结构Fe-Cu合金的生成热。计算结果表明:当Cu 原子的摩尔分数低于40%时,Fe-Cu合金晶体为BCC结构,较FCC结构更稳定;反之,当Cu 原子的摩尔分数高于40%时,Fe-Cu合金晶体为FCC结构,较BCC更稳定。LIU等[4]的第一性原理计算结果表明:当Cu原子的摩尔分数不高于50%时,BCC结构的Fe-Cu合金满足其晶体结构的Born弹性稳定性准则,并可以亚稳态形式存在。以上实验与理论研究结果表明,非平衡条件下Fe-Cu系两个端际固溶体的最大固溶度尚存在不一致性。同时,有关不同成分FCC结构Fe-Cu合金的弹性稳定性问题尚无文献报道。近年来,ZUNGER等[5]采用特殊准随机结构(SQS)方法处理无序固溶体合金,克服了平均场理论的限制,与超晶胞方法相比,提高了理论计算的效率。特殊准随机结构方法已成功应用于研究BCC和FCC固溶体合金的性能。例如,应用特殊准随机结构方法并结合第一性原理计算,JIANG等[6]及XIE和ZHAO[7]研究了BCC 结构的二元固溶体合金的基态性质、热力学性能以及结构性质。von PEZOLD等[8]研究了FCC结构Al-Ti无序固溶体合金的弹性性质,表明采用32个原子的SQS晶胞结构的计算结果与256个原子的超晶胞结构的计算结果一致。该方法也成功地应用于其他晶体结构合金和三元合金的研究,其中,WANG等[9]及JIANG和DU[10]分别研究了Mg-Si二元和γ′-Ir3(Al, W)三元固溶体合金的热力学性能。
本文作者采用SQS方法建立Cu原子摩尔分数分别为25.0%、37.5%和50.0%的 FCC结构Fe-Cu无序固溶体合金晶胞结构模型,并利用基于密度泛函理论的投影缀加波赝势和广义梯度近似方法,计算以上3种不同成分FCC结构Fe-Cu无序固溶体合金的平衡晶格常数、原子磁矩、混合热等基态性质及其弹性性质,并对不同成分FCC结构Fe-Cu无序固溶体合金的弹性稳定性进行分析与讨论。
1 计算方法
本研究采用基于密度泛函理论的VASP (Vienna ab initio simulation package)软件包进行理论计算[11],计算中采用投影缀加波赝势方法(PAW)和广义梯度近似(GGA)形式的Perdew and Wang (PW91)的势函数来描述交换相关参数[12−14]。平面波的截断能取425 eV,电子步自洽循环的能量收敛判据为1×10−6eV。采用32个原子特殊准随机结构(SQS)近似方法建立的晶胞作为FCC结构Fe-Cu无序固溶体合金的结构模型,3种不同成分合金的名义分子式分别为Fe24Cu8、Fe20Cu12和Fe16Cu16,其晶胞结构分别如图1(a)、(b)和(c)所示。所有计算均采用Monkhorst-Pack特殊k网格点方法对布里渊区进行积分[15],3种SQS晶胞的k网格点均取6×6×6。
2 计算结果与讨论
分别在无电子自旋极化和电子自旋极化条件下,对FCC结构Fe以及3种不同成分FCC结构 Fe24Cu8、Fe20Cu12和Fe16Cu16无序固溶体合金特殊准随机结构的晶格常数进行优化,不同晶格常数与晶胞能量的关系曲线如图2所示。图2表明,从能量角度分析FCC结构Fe可能存在无磁性(NM)、低铁磁性(LM)以及高铁磁性(HM)3种状态,其中FCC 结构Fe的无磁性状态能量最低,这与MORUZZI等[16]的研究结果相一致。KONG 和LIU[17]却认为Fe的低铁磁性状态能量最低。而不同成分FCC结构 Fe-Cu无序固溶体合金则只存在无磁性(NM)与铁磁性(FM)两种状态,其中铁磁性状态较无磁性状态的能量更低。
采用Murnaghan状态方程拟合各晶胞不同体积与能量关系曲线,以得到平衡晶格常数(a0)和体弹性模量(B0),如式(1)所示;并进一步计算Fe-Cu合金的混合热和磁矩,其中混合热的计算公式如式(2)所示。

式中:V0为晶胞平衡晶格体积;B0为体弹性模量;B0′为压力系数;E0为平衡体积能量。

图1 FCC 结构Fe24Cu8、Fe20Cu12和Fe16Cu16Fe-Cu无序固溶体合金的特殊准随机结构模型Fig. 1 Special quasirandom structure models of FCC structured Fe24Cu8(a), Fe20Cu12(b) and Fe16Cu16(c) random alloys (White and black balls correspond to Fe and Cu atoms, respectively)

式中:Emix为无序固溶体合金的混合热,N和M分别为合金中Fe和Cu原子的个数,E(FeNCuM)、E(FCC, Fe) 和E(FCC, Cu)分别为无序固溶体合金的能量、单个FCC结构高磁性状态Fe原子和Cu原子的能量。计算结果如表1所列。由表1可知,FCC结构Fe的平衡晶格常数、体弹性模量以及磁矩等基态性质与文献[16−17]结果有很好的一致性。此外,随着Cu含量的增加,铁磁性FCC结构 Fe-Cu无序固溶体合金的晶格常数先略有下降后又上升,体模量与磁矩则呈下降趋势。铁磁性FCC结构 Fe-Cu无序固溶体合金的混合热均为正值,且随着Cu含量的增加而增大。这说明即使在基态条件下FCC结构 Fe-Cu无序固溶体合金在能量学上仍是不稳定的,这与Fe-Cu系平衡相图是一致的。
立方结构晶体存在3个独立的弹性常数C11、C12和C44。根据Born弹性稳定性准则[19],立方结构晶体的弹性常数必须同时满足:
计算高铁磁性Fe和Fe-Cu无序固溶体合金的弹性常数时,可先对晶胞进行不同方式的弹性变形处理,然后计算出变形后晶胞的能量变化,并通过拟合能量变化与应变关系,从而得到弹性常数。分别给晶胞施加一个等体积的正应变变形和一个等体积的切应变变形,相对应的应变张量ε分别为

式中:Eortho为正应变能量;Emono为切应变能量;δ为应变,其取值范围为−0.01~0.01,步长为0.002。两种变形引起的能量变化分别为

式中:O(δ4)表示忽略高阶无穷小量。根据公式(8)和(9)可直接确定C11−C12和C44。另外,体模量和弹性常数存在以下关系:

因此,联立式(8)和(10)即可计算出C11和C12。高铁磁性FCC结构Fe和Fe-Cu无序固溶体合金的弹性常数计算结果如表2所列。从表2可以看出,高铁磁性FCC结构Fe的C44和C11–C12均为负值,与文献[18]中的理论计算值13 GPa和−76 GPa存在差异。但都说明高铁磁性FCC结构Fe的弹性常数不满足Born弹性稳定性准则。随着Cu 含量的增加,铁磁性FCC结构Fe-Cu无序固溶体合金的弹性常数C11和C44呈上升趋势,C12呈下降趋势,C11–C12也呈上升趋势。3种不同成分Fe-Cu无序固溶体合金中只有Fe24Cu8不满足Born弹性稳定性准则,Fe20Cu12和Fe16Cu16均满足Born弹性稳定性准则。正方剪切常数C11–C12随着Cu含量的增加而增大,说明FCC结构Fe-Cu无序固溶体合金的结构稳定性随着Cu 含量的增加而增加。表1的计算结果表明,随着Cu含量的增加,铁磁性FCC结构Fe-Cu无序固溶体合金的混合热均为正值,且随着Cu含量的增加而增大。从能量学角度分析,随着Cu含量的增加,铁磁性FCC结构 Fe-Cu无序固溶体合金的结构稳定性应该是降低的。但这与以上铁磁性FCC结构 Fe-Cu无序固溶体合金的弹性性质计算结果相悖。以下关于铁磁性FCC结构 Fe-Cu无序固溶体合金电子结构的计算将进一步表明在能量学上应用混合热来说明不稳定或亚稳定Fe-Cu无序固溶体合金结构稳定性的变化是失效的。

表1 FCC结构Fe和Fe-Cu无序固溶体合金的晶格常数(a0)、体模量(B0)、混合热(Emix)和磁矩(Ms)Table 1 Lattice constant (a0), bulk modulus (B0), mixing energy (Emix) and magnetic moment (Ms) of FCC Fe and Fe-Cu random alloys
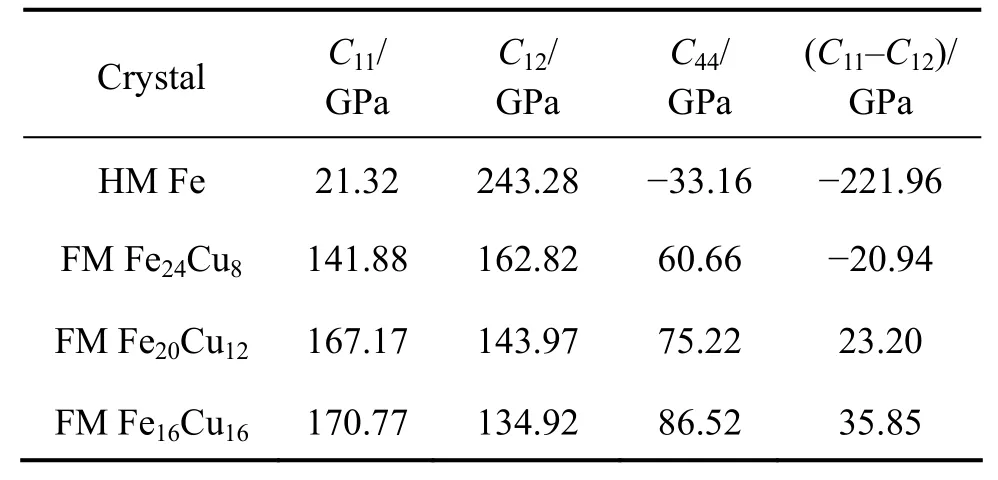
表2 高铁磁性FCC结构Fe和Fe-Cu无序固溶体合金的弹性常数Table 2 Elastic constants of FCC high ferromagnetic Fe and ferromagnetic Fe-Cu random solid solution alloys

图3 FCC结构HM Fe和FM Fe-Cu无序固溶体合金的总电子态密度(TDOS)分布Fig. 3 Total density of states (TDOS) of FCC high ferromagnetic Fe and ferromagnetic Fe-Cu random alloys: (a) HM Fe; (b) Fe24Cu8; (c) Fe20Cu12; (d) Fe16Cu16
分别计算高铁磁性FCC结构Fe以及3种不同成分Fe-Cu无序固溶体合金的总电子态密度分布,计算结果如图3所示。从图3可以看出,高铁磁性FCC结构Fe以及3种不同成分Fe-Cu无序固溶体合金的总电子态密度分布曲线的峰形十分相似,随着Cu含量的增加,态密度分布向低能区域移动,从而导致费米能以下的成键态密度增加。一般认为,合金的态密度分布中费米面位置和费米能级处态密度的大小决定该合金的结构稳定性,费米能级处态密度的数值越低,说明该合金结构越稳定[20]。图3中Fe-Cu无序固溶体合金费米能级处的自旋向上和向下两部分态密度的绝对值均随Cu含量的增加而降低,说明合金也越趋于稳定。这与以上关于铁磁性FCC结构 Fe-Cu无序固溶体合金的弹性性质计算结果一致。以上计算结果表明,3种不同成分FCC结构Fe-Cu无序固溶体合金虽然在热力学意义上是不稳定的,但是当Cu原子的摩尔分数不低于37.5%时,FCC结构Fe-Cu无序固溶体合金却可以满足Born弹性稳定性准则,并可能以亚稳态形式存在。LIU等[4]的第一性原理计算结果表明,当Cu原子的摩尔分数不高于50%时,BCC结构的Fe-Cu合金满足其晶体结构的Born弹性稳定性准则。因此,在37.5%~50%Cu成分区间内,BCC结构和FCC结构均满足Born弹性稳定性准则。GONG 等[3]有关Fe-Cu合金生成热的计算结果表明,当Cu 原子的摩尔分数低于40%时,Fe-Cu合金晶体为BCC结构较FCC结构更稳定;反之,当Cu 原子的摩尔分数高于40%时,Fe-Cu合金晶体为FCC结构,较BCC结构更稳定。然而,文献所报道的实验研究表明,在很宽的成分区间内,BCC结构Fe-Cu无序固溶体合金比FCC结构Fe-Cu无序固溶体更稳定,这与合金的制备方法密切相关。例如,气相淬火方法可以使BCC结构Fe-Cu合金中Cu原子的摩尔分数达到50%[21],机械合金化方法也可使FCC结构Fe-Cu无序固溶体合金中Cu 原子的摩尔分数降低至约30%[1],这说明本文作者的计算结果是可靠的,同时,利用晶体结构的Born弹性稳定性准则来判断合金亚稳态存在的成分边界是有效的。
3 结论
1) 从能量学上分析,FCC 结构Fe存在无磁、低铁磁和高铁磁性3种状态,而FCC 结构Fe-Cu无序固溶体合金仅存在无磁与铁磁性2种状态。
2) 高铁磁性FCC结构Fe不满足Born弹性稳定性准则。
3) 铁磁性FCC结构Fe-Cu无序固溶体合金的弹性稳定性随着Cu 含量的增加而增强,当Cu 原子的摩尔分数高于37.5%时,合金满足Born弹性稳定性准则。
REFERENCES
[1]黄建宇, 吴玉琨, 胡魁毅, 孟祥敏. 机械合金化诱导Fe-Cu系固溶度的扩展 [J]. 金属学报, 1993, 29(2): 60−63. HUANG Jian-yu, WU Yu-kun, HU Kui-yi, MENG Xiang-min. Extension of solid solubility induced by mechanical alloying in Fe-Cu system [J]. Acta Metallurgica Sinica, 1993, 29(2): 60−63.
[2]KOBAYASHI S, TAKEDA T, NAKAI K, HAMADA J I, KANNO N, SAKAMOTO T. Effect of Nb addition on Cu precipitation in ferritic stainless steel [J]. ISIJ International, 2011, 51(4): 657−662.
[3]GONG H R, KONG L T, LIU B X. Structural stability and magnetic properties of metastable Fe-Cu alloys studied by ab initio calculations and molecular dynamics simulations [J]. Physical Review B, 2004, 69(5): 54203−54210.
[4]LIU J Z, van de WALLE A, GHOSH G, ASTA M. Structural, energetic, and mechanical stability of Fe-Cu bcc alloys from first-principles calculations [J]. Physical Review B, 2005, 72(14): 144109−144123.
[5]ZUNGER A, WEI S H, FERREIRA L G, BERNARD J E. Special quasirandom structure [J]. Physical Review Letters, 1990, 65(3): 353−356.
[6]JIANG C, WOLVERTON C, SOFO J, CHEN L Q, LIU Z K. First-principles study of binary bcc alloys using special quasirandom structure [J]. Physical Review B, 2004; 69(21): 214202−214211.
[7]XIE Y P, ZHAO S J. The energetic and structural properties of bcc NiCu, FeCu alloys: A first-principles study [J]. Computational Materials Science, 2011, 50(9): 2586−2591.
[8]von PEZOLD J, DICK A, FRIÁK M, NEUGEBAUER J. Generation and performance of special quasirandom structures for studying the elastic properties of random alloys: Application to Al-Ti [J]. Physical Review B, 2010, 81(9): 94203−94209.
[9]WANG A J, ZHOU L C, KONG Y, DU Y, LIU Z K, SHANG S L, OUYANG Y F, WANG J, ZHANG L J, WANG J C. First-principles study of binary special quasirandom structures for the Al-Cu, Al-Si, Cu-Si, and Mg-Si systems [J]. CALPHAD: Computer Coupling of Phase Diagrams and Thermochemistry, 2009, 33(4):769−773.
[10]JIANG C, DU Y. Thermodynamic and mechanical stabilities ofγ´-Ir3(Al, W) [J]. Journal of Applied Physics, 2011, 109(2): 23504−23513.
[11]KRESSE G, FURTHMÜLLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set [J]. Physical Review B, 1996, 54(16): 11169−11186.
[12]KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Physical Review B, 1999, 59(3):1758−1775.
[13]BLÖCHL P E. Projector augmented-wave method [J]. Physical Review B, 1994, 50(24):17953−17979.
[14]PERDEW J P, CHEVARY J A, VOSKO S H, JACKSON K A, PEDERSON M R, SINGH D J, FIOLHAIS C. Atoms, molecules, solids, and surfaces: Application of the generalized gradient approximation for exchange and correlation [J]. Physical Review B, 1992, 46(11): 6671−6687.
[15]MONKHORST H J, PACK J D. Special points for Brillouinzone integrations [J]. Physical Review B, 1976, 13(12): 5188−5192.
[16]MORUZZI V L, MARCUS A H, SCHWARZ K, MOHN P. Ferromagnetic phases of bcc and fcc Fe, Co and Ni [J]. Physical Review B, 1986, 34(3): 1784−1791.
[17]KONG L T, LIU B X. Distinct magnetic states of metastable fcc structured Fe and Fe-Cu alloys studied by ab initio calculations [J]. Journal of Alloys and Compounds, 2006, 414(1/2): 36−41.
[18]PAXTON A T, ELSÄSSER C. Electronic structure and total energy of interstitial hydrogen in iron: Tight binding models [J]. Physical Review B, 2010, 82(23): 235125−235139.
[19]BORN M, HUANG K. Dynamical theory of crystal lattices [M]. Oxford: Clarendon Press, 1954: 141.
[20]HONG T, WATSON-YONG T J, FREEMAN A J. Crystal structure, phase stability, and electronic structure of Ti-Al intermetallics: TiAl3[J]. Physical Review B, 1990, 41(18): 12462–12467.
[21]KEUNE W, LAUER J, WILLIAMSON D L. Mössbauer studies of FeCu thin films [J]. Journal de Physique, 1974, 35(12): 473–476.
(编辑 陈卫萍)
Elastic stability of face-centered cubic Fe-Cu random solid solution alloys based on special quasirandom structure model
WEN Yu-feng, SUN Jian, HUANG Jian
(School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)
The first-principles method based on projector augmented wave pseudo-potential and generalized gradient approximation was employed to calculate the ground state properties, elastic constants and electronic structure of face-centered cubic (FCC) Fe and Fe-Cu random solid solution alloys with Cu contents of 25%, 37.5% and 50% (mole fraction). The special quasirandom structure (SQS) models were selected as the computational models for FCC Fe-Cu random solid solution alloys. The calculated total energies show that a nonmagnetic, a low ferromagnetic and a high ferromagnetic state are obtained in the FCC Fe, whereas a nonmagnetic state and a high ferromagnetic state exist in the ferromagnetic FCC Fe-Cu random solid solution alloys. The high ferromagnetic FCC Fe does not satisfy Born’s criterion of elastic stability. The elastic stability of ferromagnetic FCC Fe-Cu random solid solution alloys increases with increasing the Cu content. When the Cu content is not less than 37.5%(mole fraction), the ferromagnetic FCC Fe-Cu random solid solution alloys satisfy Born’s criterion of elastic stability, and can exist as the metastable phases.
Fe-Cu random solid solution alloy; special quasirandom structure; elastic property; first-principles
TG146.2
A
国家自然科学基金资助项目(50931003, 50871065);上海市科委资助项目(09JC1407200, 10DZ2290904)
2011-08-30;
2012-02-12
孙 坚,教授,博士;电话:021-54745593;E-mail: jsun@sjtu.edu.cn
1004-0609(2012)09-2522-07
