浅谈公路设计中缓和曲线的选用

冯心宜

(广东省公路勘察规划设计院股份有限公司，广东广州 510507)

缓和曲线是构成公路平面线形的基本要素之一，它是设置在直线与圆曲线之间、或半径相差较大的两个同向圆曲线之间的一种曲率连续变化的曲线。

缓和曲线在公路设计中，主要起以下作用:

①曲率连续变化，便于车辆遵循;

②离心加速度逐渐变化，旅客感觉舒适;

③超高横坡度逐渐变化，行车更加平稳;

④与圆曲线配合得当，增加线形美观。

在我国现行《公路工程技术标准》中，采用回旋线作为缓和曲线。以下从缓和曲线的四点主要作用入手，以回旋线的相关理论公式为基础，对公路设计过程中缓和曲线的选用提出一些建议。

1 缓和曲线选用应考虑线形曲率过渡要求

1.1 为满足曲率过渡对缓和曲线长度的要求

汽车在转弯行驶过程中，存在一条曲率连续变化的轨迹线，轨迹线的长度由车辆行驶速度、曲率变化幅度，以及驾驶员转动方向盘的速度确定;为保证有一条易于遵循的路线，避免车辆在转弯过程中侵入相邻车道，必须确保缓和曲线有一定的长度;若缓和曲线过短，驾驶员就必须快速地完成方向盘操作，特别在高速行驶时容易引发危险。

一般认为，驾驶员往一个方向转动方向盘的时间至少需要3 s，因此缓和曲线选用时，其长度至少应满足车辆特定运行速度下3 s行程。

1.2 卵形曲线中缓和曲线长度的计算

缓和曲线即回旋线的基本计算公式为:

式中:r为回旋线上某点的曲率半径，m;l为回旋线上某点到原点的曲线长，m;A为回旋线参数，m。

当平曲线为直线—回旋线—圆曲线的基本型时，回旋线长度的计算公式如下:

式中:R为回旋线所连接的圆曲线半径，m;LS为回旋线长度，m。

但当缓和曲线为连接同向圆曲线的卵形曲线组成部分时，以上式(2)将不再适用，此时可采用缓和曲线的基本定义“满足曲率过渡要求”将式(2)中的半径转换为用曲率表示:

式中:R1为卵形曲线小圆半径，m;R2为卵形曲线大圆半径，m。

由于在目前的高速公路特别是互通立交设计过程中，卵形曲线作为一种重要的平面线形被广泛采用，因此了解以上计算方法对设计过程中缓和曲线的选用具有重要意义，如某立交匝道范围的卵形曲线R1=200 m，R2=400 m，A=200 m，则计算所得LS=100 m。

2 缓和曲线选用应考虑乘客舒适性要求

缓和曲线对乘客舒适性要求的满足，主要体现在车辆转弯时离心加速度变化的快慢;若变化过快，将会使乘客有不舒适感;为使乘客舒适，缓和曲线需要有一定的长度保证;离心加速度的变化可用离心加速度变化率表示:

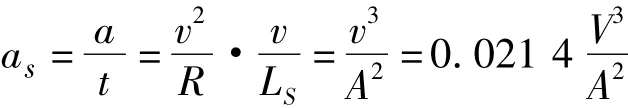
式中:v为车辆在回旋线上的运行速度，m/s;V为车辆运行速度，km/h;as为离心加速变化率，m/s3。

离心加速度变化率的取值:离心加速度变化率的取值，直接影响司乘人员的舒适性，各国采用的标准并不相同，我国铁路上一般取值不大于0.3 m/s3，而公路主线上取值一般不大于0.6 m/s3。而对于公路互通立交的匝道范围，由于运行速度相对较低，可参考表1。

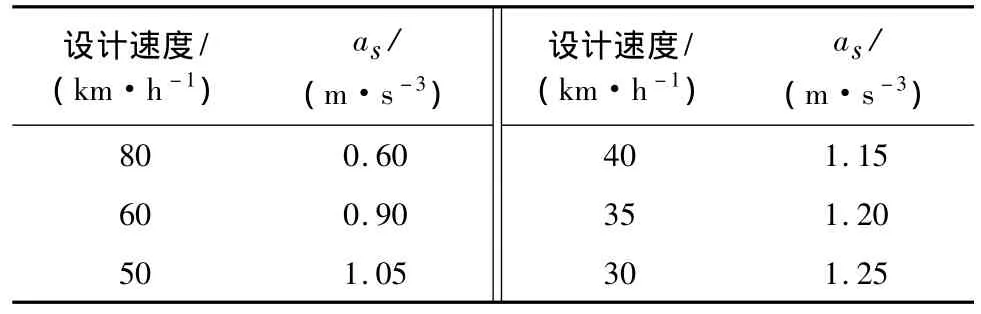
表1 离心加速度取值范围

离心加速度变化对公路设计的影响，主要的一方面体现在高速公路互通立交出口设计过程中;由于高速公路主线一般设计速度高、线形指标高，而立交匝道范围设计速度低、指标低，因此主线与匝道相接的连接部范围往往成为事故多发区，而这与连接部附近回旋线参数的取值也有一定的关系。

一般情况下，当车辆由高速公路主线驶出进入匝道范围时，连接部附近通常采用回旋线作为两侧高低线形指标间的过渡;经验表明，当连接部路段线形的设计速度不小于主线设计速度的70%时可确保行车安全;也就是说，当主线设计速度为100 km/h，匝道设计速度为40 km/h，连接部处回旋线参数的取值，也必须按不小于设计速度70 km/h的指标选取，若低于此标准，则将造成线形指标过渡太急、离心加速度变化率过大，司乘人员会感觉车辆明显的外倾趋势，可能引起车辆未及时减速及转向而引发事故。

参考式(4)及表1，可计算得出高速公路互通立交出口连接部附近回旋线参数的最小值(表2)。

表2 互通立交出口连接部处回旋线最小参数

如图1所示，某高速公路B型喇叭立交，主线设计速度为100 km/h，设置有C匝道、E匝道两处出口匝道，出口端回旋线参数分别为144 m及75 m，代入式(4)计算。

计算所得，在保证乘客舒适性及运行安全的前提下，A=144 m对应的运行速度为83.5 km/h＞70 km/h;A=75 m对应的运行速度为54.0 km/h＜70 km/h。

因此C匝道的出口回旋线参数取值满足运行安全的要求，而E匝道出口端的回旋线参数对应的运行速度过低，主线上的出口车流到达时并未能确保充分减速至54 km/h，容易引发事故。

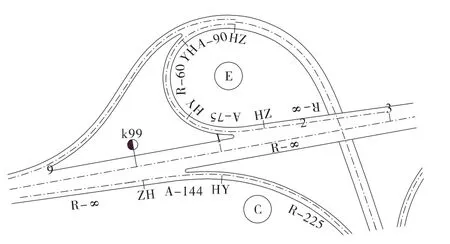
图1 某B型喇叭立交主线出口设计

以出口端安全运行速度70 km/h，缓和曲线参数A=75 m代入式(4)计算，所得离心加速度变化率as=1.305 m/s3，超出表1中所列的离心加速度取值范围。

对于以上情况，应调整E匝道设计，可考虑:

1)加大回旋线参数;

2)由于B型喇叭立交加大回旋线参数后容易引起立交规模增加过多，此时可通过增加减速车道长度、或设置减速标志标线等交通安全设施，确保车辆在充分减速后再驶入匝道范围。

3 缓和曲线选用应满足超高渐变率适中要求

公路设计时，对于超高横坡的渐变，一般是在缓和曲线范围内完成;如果缓和曲线过短、超高渐变率过大，则路面将由于横坡的急剧变化呈现明显扭曲;若缓和曲线过长、超高渐变率过小，则可能导致路面整体横坡过于平缓，对排水不利;当缓和曲线长等于超高渐变段长时，其计算公式如下:

同时，式(5)也可转换为:

式中:B为超高旋转轴至路面边缘宽度，m;Δi为超高横坡的变化值;p为超高渐变率，即路面边缘的附加坡度。

以下主要结合以上公式，对公路纵坡平缓路段，超高渐变段及缓和曲线长度选用对路面排水的影响进行分析。

图2所示为某公路路面等高线图，该路段路线从左到右，起点处路面横坡为2%，终点横坡为0%，终点处设计高程为0，路段纵坡为－0.5%，设置有中央分隔带，单幅路面宽度为10.0 m，以中央分隔带边缘作为超高旋转轴，超高渐变段总长60 m。

图2 某公路路面等高线图

本路段左幅路面在超高渐变过程中逐渐抬高，右幅路面则逐渐降低，同时本路段设置有－0.5%的纵坡，纵坡与横坡的变化在两幅路面均分别形成一个曲面，图2中示意出了曲面上的等高线分布。

同时根据公式(6)，还可计算得出路面上与超高旋转轴距离不同的各点沿路线前进方向的实际纵坡，见表3。

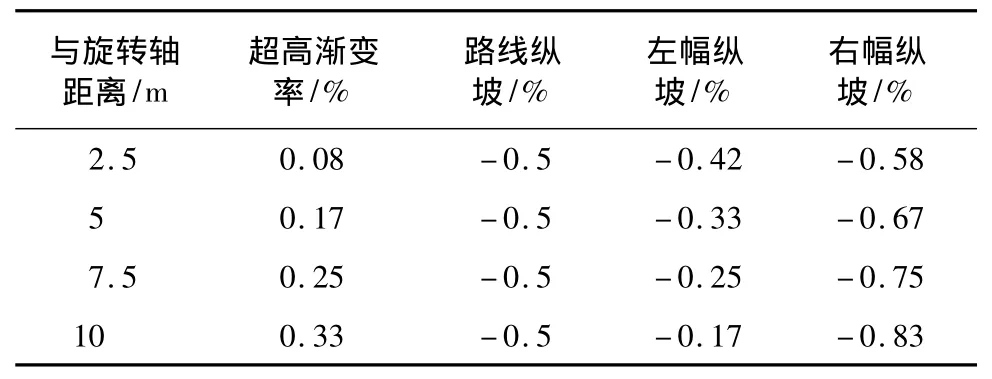
表3 超高渐变段与纵坡叠加后的路面纵坡情况

如图2及表3所示，由于路线左幅超高附加的纵坡度与路段纵坡相互抵消，导致左幅路面各部分的实际纵坡小于路段纵坡，路面等高线较疏，排水不畅;而右幅则由于附加纵坡与路段纵坡方向相同，加大了路面的实际纵坡，加速了路面排水。

因此在公路设计过程中，应尽量避免路线纵坡缓坡段与超高渐变段的重合;若确实需要重合时，应通过计算，尽可能加大纵坡坡率，并合理选择缓和曲线长度及超高渐变段长度，绘制路面等高线图，避免局部路段排水不畅引起运营期的积水，造成交通事故。

4 缓和曲线选用应满足线形美观的要求

公路设计过程中，缓和曲线的选用还必须满足公路线形美观的要求，这主要是通过缓和曲线角即回旋线切线角来控制。

当公路平面的圆曲线半径较大时，其超高值往往较小，超高渐变所需的缓和曲线长度也较短，当缓和曲线长度过短，导致缓和曲线角小于3°时，缓和曲线在视觉上很容易被忽略;当圆曲线半径较小、超高渐变所需的缓和曲线长度较长，导致缓和曲线角大于29°时，缓和曲线与圆曲线的搭配将不容易协调。

因此公路设计过程中，缓和曲线角的取值一般在3°～29°之间，由此推算出缓和曲线参数的取值。缓和曲线角的计算公式为:

公式可转换为:

将缓和曲线角等于3°及29°，代入以上公式，可得出:

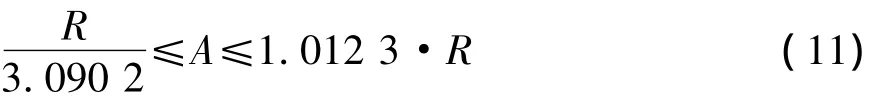
因此，在现行《公路路线设计规范》中规定:

当R较小、接近100 m时，可采用较大的缓和曲线角，即取A=R;当R较大时，可选择A接近R/3;但当R超过3 000 m时，此时圆曲线的曲率较小，即使同时加大A，其景观效果也接近，变化不明显，因此A可小于R/3。

在公路路线设计过程中，特别是高速公路平面设计中，更多的是采用式(10);主要是由于高速公路的线形指标普遍较高、圆曲线半径普遍较大，因此在缓和曲线长度选用时，一般倾向于R≤9LS。

在理解了缓和曲线与圆曲线搭配如何确保线形舒适及美观的内涵后，在公路设计过程中，还可结合地形地物、路线技术标准等不同的建设条件，合理确定不同路线路段的缓和曲线角取值，从而合理选定缓和曲线参数。

5 结语

缓和曲线是公路平面设计过程中的基本线形，它介于直线与圆曲线之间、或反向的圆曲线之间，往往是作为圆曲线与直线的补充出现，其对地形条件变化的适应性不如直线与圆曲线，但却有其自身的功能与作用;在公路设计过程中，缓和曲线的选用经常容易被设计者所忽略。

本文从缓和曲线的基本定义及理论公式出发，结合实际工作经验，对缓和曲线的功能逐层剖析，归纳出公路设计中不同情况下缓和曲线选用的方式方法。

公路的建设条件千变万化，在设计过程中，若仅依赖相关规范、标准的文字条文，在遇到特殊情况时往往会难以抉择，因此只有理解了线形、指标的真正含义后，才能做到因地制宜、灵活设计。

［1］JTG B01－2003，公路工程技术标准［S］.

［2］JTG D20－2006，公路路线设计规范［S］.

［3］日本道路公团，交通部工程管理司译制组译.日本高速公路设计要领——几何设计·休息设施［M］.西安:陕西旅游出版社，1991.

［4］张雨化.道路勘测设计［M］.北京:人民交通出版社，1997.

［5］霍 明.公路路线设计细则(总校稿)［Z］.西安:中交第一公路勘察设计研究院有限公司，2009.