对个人外汇理财产品初始价格的研究

陈 颖，王小灵

(南京财经大学 应用数学学院， 江苏 南京 210046)

0 引言

20世纪90年代中后期以来, 个人外汇理财业务逐渐成为国内银行的主要金融衍生产品[1-3]。近年来, 国内银行又陆续推出了品种繁多的个人外汇理财新产品。 我们知道所有这些产品的收益率主要受外汇利率、汇率波动的影响,因此购买此类产品的投资者一般是对未来汇率走势有明确预期。 徐承龙等研究了在两国利率均为常数情况下, 通过偏微分方程的方法，对交通银行“智汇宝”理财产品的合约价值进行了定价[4], 但他未考虑违约的情况。 本文将在此基础之上, 以工行“两得利”外汇理财产品为例，考虑违约的情况对该理财产品的合约价值进行定价。

1 模型建立

为简化问题，设存款为1单位A外汇。 并作如下假设：

1) 美元对外汇的汇率为S(t) (1单位美元兑换1单位A外汇的数量)服从几何Brown运动

(1)

其中σ1为波动率,r2为美元的无风险利率,rt为A外汇的无风险利率, 且满足Vasicek模型

drt=a(θ-rt)dt+σ2dWt

(2)

P(r,t;T)=A(T)e-rB(t)

(3)

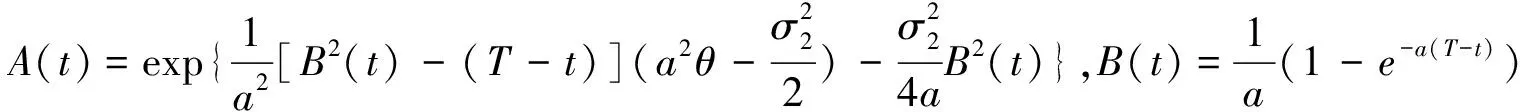
2)设V为一单位A外汇存款合约的价值,V是关于汇率St，A外汇随机利率rt和时间t的函数, 即V=V(S,r,t)。 理财产品合约的初始时刻记为t=0, 合约到期日记为t=T。V0=V(S0,r,0)为初始时刻该理财产品的合约价值[1]。

3) A外汇存款的协定年利率为正的常数r4, 协定汇率为正的常数K。期权金的年收益率为正的常数r3。

4)市场是公平的、透明的, 即不存在无风险套利机会。

5)银行只有在到期日t=T才支付给客户收益, 即不考虑银行违约。 如果客户没有赎回本金, 那么到期日, 客户的最终收益主要取决于银行是否执行期权。 客户到期日的收益为

(4)

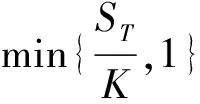
6)如果客户在合约存续期内选择赎回本金, 则客户可以获得一部分A外汇本金。 假设客户的违约强度λ为正的常数, 违约时间t服从概率密度函数为q(t)=λe-λ(T-t)的分布, 那么该理财产品合约的价格就是依赖于违约时间的数学期望。 客户在τ时刻的收益为V(S,r,t)=ω,这里ω为常数回收率, 0<ω<1。

7)市场是无摩擦的, 即不考虑税收和交易费用。构造这样的投资组合: 买入一份理财产品V, 卖出Δ1t份美元(折算为Δ1tS份A外汇)， 同时卖出Δ2t份A国零息票债券

π=V-Δ1tS-Δ2tP

(5)

选取适当的Δ1t和Δ2t使得该投资组合在[t,t+dt]内是无风险的, 同时考虑到美元有利息收入Δ1tStr2dt, 故

πt+dt=Vt+dt-Δ1tSt+dt-Δ1tStr2dt-Δ2tPt+dt

(6)

根据无套利原理：dπt=rtπtdt，由(5)、(6)可得

dVt-Δ1tdSt-Δ1tStr2dt-Δ2tdPt=rt[Vt-Δ1tSt-Δ2tPt]dt

(7)

而对(5)运用多维Ito公式[3], 可得

(8)

由假设(1)中的(3)式，则

(9)

(10)

如果考虑违约风险，违约时间τ服从概率密度函数为q(τ)=λe-λ(T-τ)的分布, 那么该理财产品合约的价值就是依赖于违约时间的数学期望[3]。

2 模型的求解

为方便起见，将以上方程的解分解为两部分[5]：

V(S,r,t)=V1(S,r,t)-V2(S,r,t)

(11)

由(10)(11)可得，V1,V2分别满足

(12)

(13)

显然方程(12)有解

V1(S,r,t)=[1+(r3+r4)T]P(r,t;T)

(14)

它可以看做t=T时刻固定收益V1(S,r,T)在当前的贴现。

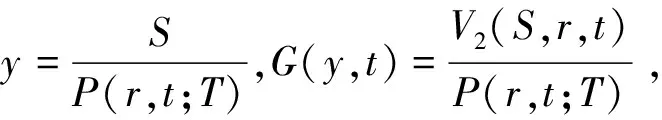
(15)

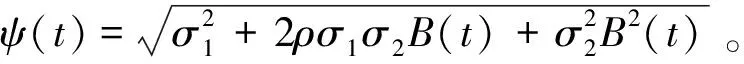
再令

W(y,t)=KG(y,t)

(16)

将式(16)带入式(15)可得

(17)

方程(17)可看做推广的看跌期权，则

W(y,t)=KN(d1)-ye-r2(T-t)N(d2)

(18)

其中

将式(18)带入式(16)可得

(19)

故

(20)

从而由式(14)和式(20)可得

(21)

如果违约情况发生, 即τ

(22)

其中

3 数值分析

下面讨论V0的价值与各参数之间的关系。

1)在不同违约强度下，初始时刻合约价值V0和初始汇率S0之间的关系。

取a=0.4,T=4,t=0,θ=0.1,σ1=0.15,σ2=0.25,K=0.7,r=0.03,ρ=0.25,

r3=0.12,r4=0.002,r2=0.001,w=0.9,运用MATLAB作图1所示：

从上图可以看出, 初始汇率越大, 则合约价值越高。 这是因为初始汇率越大, 银行执行期权的概率就越小, 而客户可以获得稳定的期权费, 故合约价值会变高。 同时可以看出, 客户的违约强度越高, 合约价值越低。 这是因为客户一旦违约, 不仅损失了期权费和固定利息, 而且只能收回部分本金。

2)在不同回收率水平下，初始时刻合约价值V0和汇率波动率σ1之间的关系。

取a=0.4,T=3,t=0,θ=0.1,σ2=0.3,K=0.7,r=0.03,ρ=0.25,r3=0.12

r4=0.002,r2=0.001,λ=0.005,S0=0.6,运用MATLAB作图2所示：

图1 V0的价值与各参数之间的关系 图2 价值V0和汇率波动率σ1之间的关系

由上图可得, 汇率波动率越大, 合约价值越低。 这是因为汇率波动率越大, 银行执行期权的可能性越大, 客户承担的风险变大, 合约价值变低。 同时可以看出, 美元回收率越高,合约价值越高。 这是因为回收率是最低收益的保证, 回收率越大, 客户违约的成本就越小,合约价值就越高。

[参考文献]

[1] Hull, J. M. and White, A..The impact of default risk on the prices of options and other derivative securities[J] .Journal of Finance,1995,40(1):53-85.

[2] Duffie D., Singleton K..Modeling Term Structures of Default Bonds [J],Review of Financial studies,1999,12(4):687-720.

[3] 姜礼尚.期权定价的数学模型和方法[M].2版.北京: 高等教育出版社,2003.

[4] 姜礼尚, 徐承龙, 任学敏,等.金融衍生产品定价的数学模型与案例分析[M].北京:高等教育出版社, 2008(6):106-114.

[5] 张寄洲.金融数学教程[M].北京：人民邮电出版社，2006:82-89.