二阶非线性边值问题的正解
2012-09-25赵冬霞孔令彬
赵冬霞,孔令彬
(1.东北石油大学 数学科学与技术学院,黑龙江 大庆 163318;2.大庆师范学院 数学科学学院,黑龙江 大庆 163712)
0 引言
本文研究二阶非线性边值问题
u″(t)-αu′(t)+βu(t)=-f(t,u(t))
(1)
u(0)=0,u(1)=0
(2)
这里α>0,0<4β-α2<π2。
二阶非线性边值问题出现在物理与应用数学等领域中,其正解具有实际意义。一些作者曾研究过含参数的二阶非线性边值问题,但含双参数的二阶非线性边值问题的结果尚不多见[1-2]。本文研究非线性二阶边值问题(1)(2),在非线性项满足超线性或次线性的条件下,证明了正解的存在性。
在f(t,u)非奇异的情形下,本文假设如下:
(H1)f(t,u)在[0,1]×[0,+∞)上非负连续;
此时称函数u(t)为边值问题(1)(2)的一个正解,如果它满足:u(t)∈C1[0,1]∩C2(0,1),且在(0,1)内u(t)>0;u(t)在(0,1)内满足(1)并满足(2)。
在f(t,u)奇异的情形下,本文假设如下:
(H5) 对几乎所有的t∈[0,1],f(t,u)关于u(t)≥0单调非增,并且
此时称函数u(t)为边值问题(1)(2)的一个正解,如果它满足u∈C1[0,1],u(0)=0,u(1)=0;u″(t)在[0,1]上几乎处处存在并且可积,并且在[0,1]上
u″(t)-αu′(t)+βu(t)=-f(t,u(t))a.e.
本文的主要结果是:
定理1:假设(H1),(H2)或(H1),(H3)成立,则边值问题(1)(2)至少存在一个正解。
1 边值问题(1)(2)的等价形式Green函数估计
(3)
这里


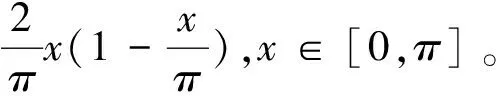


于是


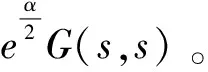

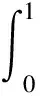
则∀u∈K有



因此Φu∈K,即Φ(K)⊂K,另外易证Φ全连续。
为证明定理1,需要如下的锥不动点定理[3]。
引理2:设E是Banach空间,K⊂E是E中的锥,Ω1,Ω2都是E中的开子集,
⊂Ω2,又设
全连续。如果
1)‖Φu‖≤‖u‖,u∈K∩∂Ω1,并且‖Φu‖≥‖u‖,u∈K∩∂Ω2;或
2)‖Φu‖≥‖u‖,u∈K∩∂Ω1,并且‖Φu‖≤‖u‖,u∈K∩∂Ω2。
2 定理1的证明
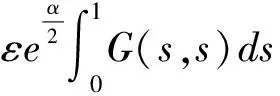
Φu(t)≤
≤

即有‖Φu‖≤‖u‖。


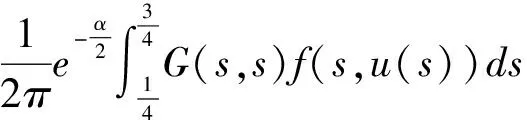

即有‖Φu‖≥‖u‖。



即‖Φu‖≥‖u‖。


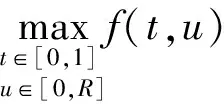
令Ω2={u∈C[0,1];‖u‖ 即有‖Φu‖≤‖u‖。 即‖Φu‖≤‖u‖。 对一类含双参数的二阶边值问题进行了研究,利用锥不动点定理,并结合Green 函数性质,在非线性项满足超线性或次线性的条件下,证明了其边值问题正解的存在性。 [参考文献] [1] Li Yongxiang.Positive solutions of fourth-order boundary value problem with two parameters[J].J.Math.Anal.Appl.,2003,281:477-484. [2] Jiang Daqing.Optimal existence theory for single and multiple positive solutions to fourthorder periodic value problems[J].Nonlinear Analysis:Real World Applications,2006(7):841-852. [3] L.H.Erbe,Wang Haiyan.On the existence of positive solutions of ordinary differential Equations[J].Proc.Amer.Math,1994,120:743-748.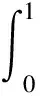
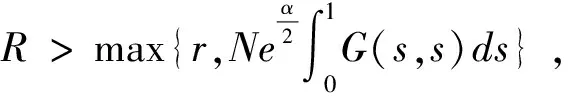
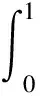
3 结语
