两种带形状参数的三角曲线

严兰兰， 梁炯丰， 黄 涛

（1. 东华理工大学数学与信息科学学院，江西 抚州 344000；

2. 东华理工大学土木与环境工程学院，江西 抚州 344000）

两种带形状参数的三角曲线

严兰兰1， 梁炯丰2， 黄 涛1

（1. 东华理工大学数学与信息科学学院，江西 抚州 344000；

2. 东华理工大学土木与环境工程学院，江西 抚州 344000）

定义了带形状参数的三次三角多项式曲线和三次三角样条曲线。前者具有与二次Bézier曲线类似的端点性质，但逼近性比二次Bézier曲线更好，且在拼接时能达到更高阶的连续性。而后者与二次 B样条曲线类似，其每一段由相继的三个控制顶点生成。对于等距节点，在一般情况下曲线C2连续，在特殊条件下可达C3连续。

计算机应用；三角基；样条曲线；形状参数

曲线曲面设计是计算机辅助几何设计的一个重要研究课题，现今较成熟的是非均匀有理B样条(NURBS)方法，但NURBS在形状设计中依然存在一些局限。为此，人们试图在非多项式函数空间寻找新的曲线。文献[1]构造了C3连续的二次三角多项式曲线；文献[2]和[3]分别研究了带一个形状参数的二次和三次三角多项式曲线；文献[4]构造了控制顶点数分别为3、4和5时的T-B样条曲线；文献[5]构造了G1连续的三次三角多项式样条曲线，特殊条件下可达到G3连续；文献[6]构造了类似于三次 Bézier曲线的含参数的三次三角多项式曲线；文献[7]构造了G3连续的三次三角多项式样条曲线，特殊条件下可达到G5连续。

这里在空间 {1 ,sint, c ost, s in2t, c os2t, s in3t,cos3t}上定义了两种新曲线。由于含形状参数，所以可以在不改变控制顶点的情况下对新曲线的形状进行调整。与二次Bézier曲线类似，所构造的三角多项式曲线也由三个控制顶点生成，且曲线插值于控制多边形首末端点并与端边相切，但该曲线对控制多边形的逼近性比二次 Bézier曲线更好。另外，两条二次Bézier曲线在拼接时至多G1连续，而两条新曲线在拼接时，只要端点之间满足G1连续条件，曲线就会自动达到G3连续，特殊条件下还可达G5连续。与二次B样条曲线类似，所构造的三角样条曲线的每一段由相继的三个控制顶点生成，但二次均匀B样条曲线只有C1连续，而对于等距节点，新曲线C2连续，特殊情况下可达C3连续。当形状参数满足一定条件时，新曲线具有比二次B样条曲线更好的对控制多边形的逼近性。

1 三角多项式曲线

1.1 基函数的构造与性质

定义 1 对t∈ [ 0,π]， λ ∈[- 2 ,1]，称函数2组

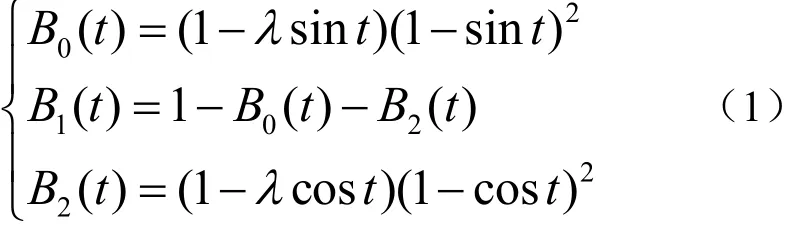
为带参数的三次三角多项式基函数，简称λB基。

λB基具有下列性质

3） 端点性质

1.2 曲线的定义与性质

为带参数的三次三角多项式曲线，简称λB曲线。由λB基的性质易知λB曲线具有对称性、凸包性、几何不变性等。另外λB曲线还具有端点性质

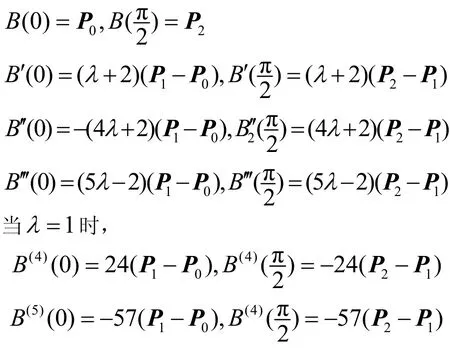
1.3 曲线的逼近性

由于B0(t)与B2(t)关于λ单调递减，故由式(3)可知：λ越大，λB曲线与点P1靠得越近。即随着λ的增大，λB曲线逐渐靠近其控制多边形。

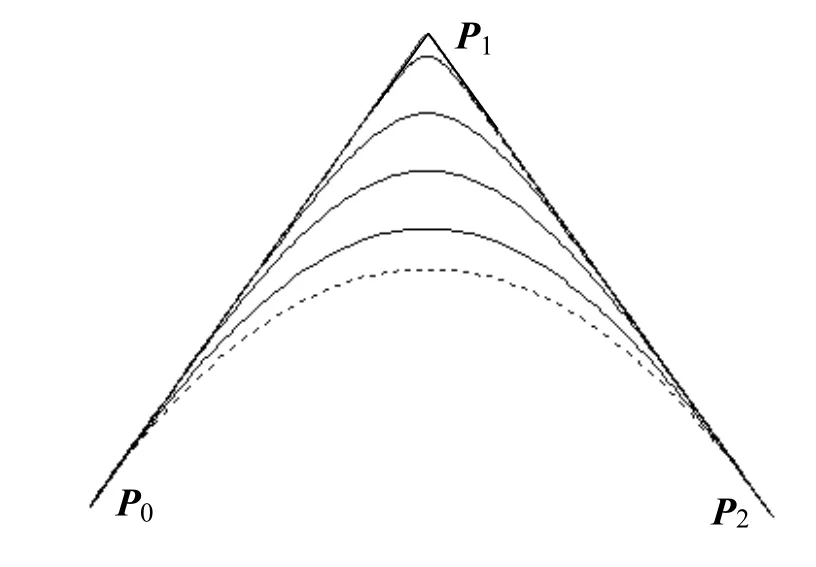
图1 取不同参数值时的Bλ-曲线

1.4 曲线的拼接

图2 两段曲线的 G3 , G5 , C1 , C2拼接图

图3 两段曲线的C 3拼接图

2 三角样条曲线

2.1 曲线的构造

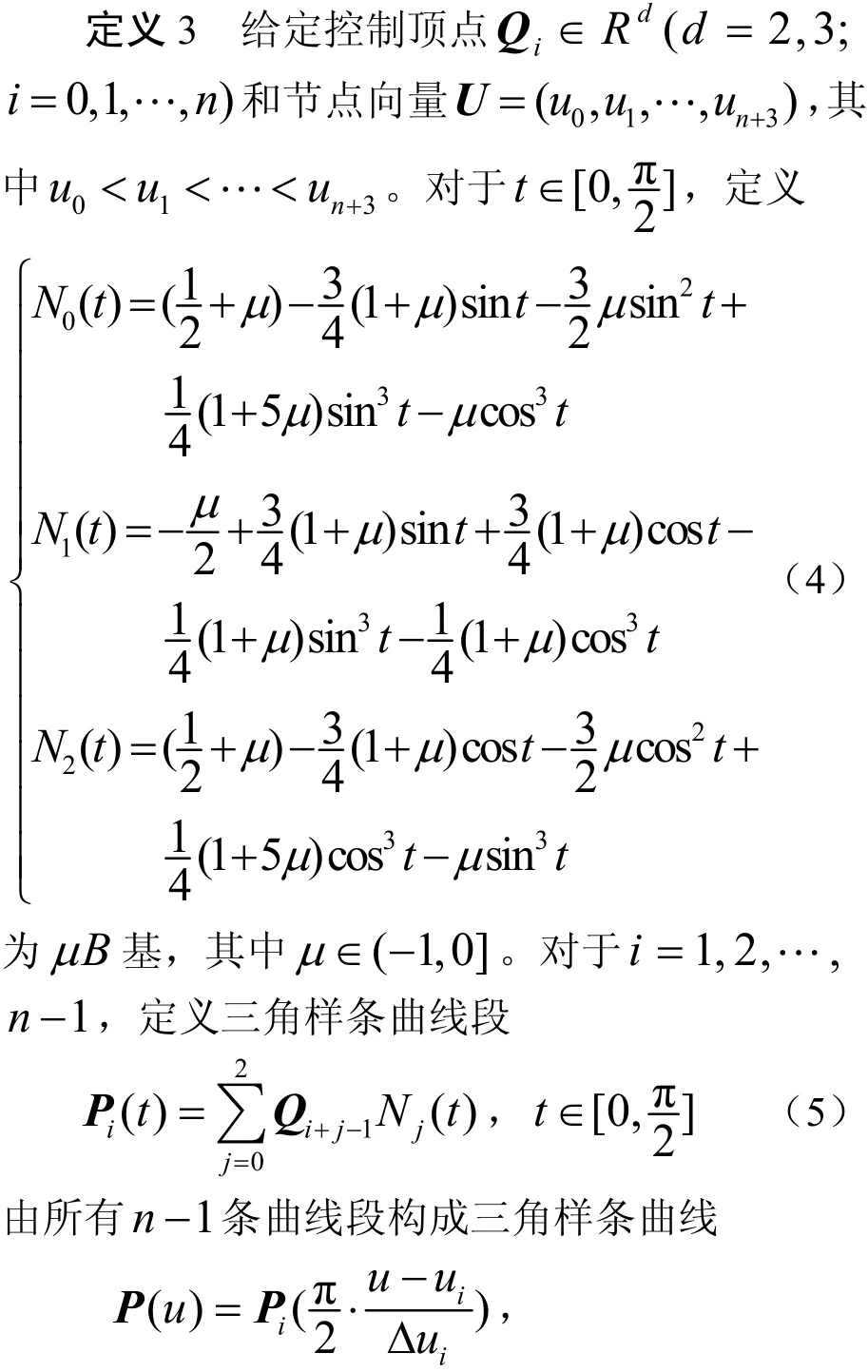
2.2 曲线的连续性

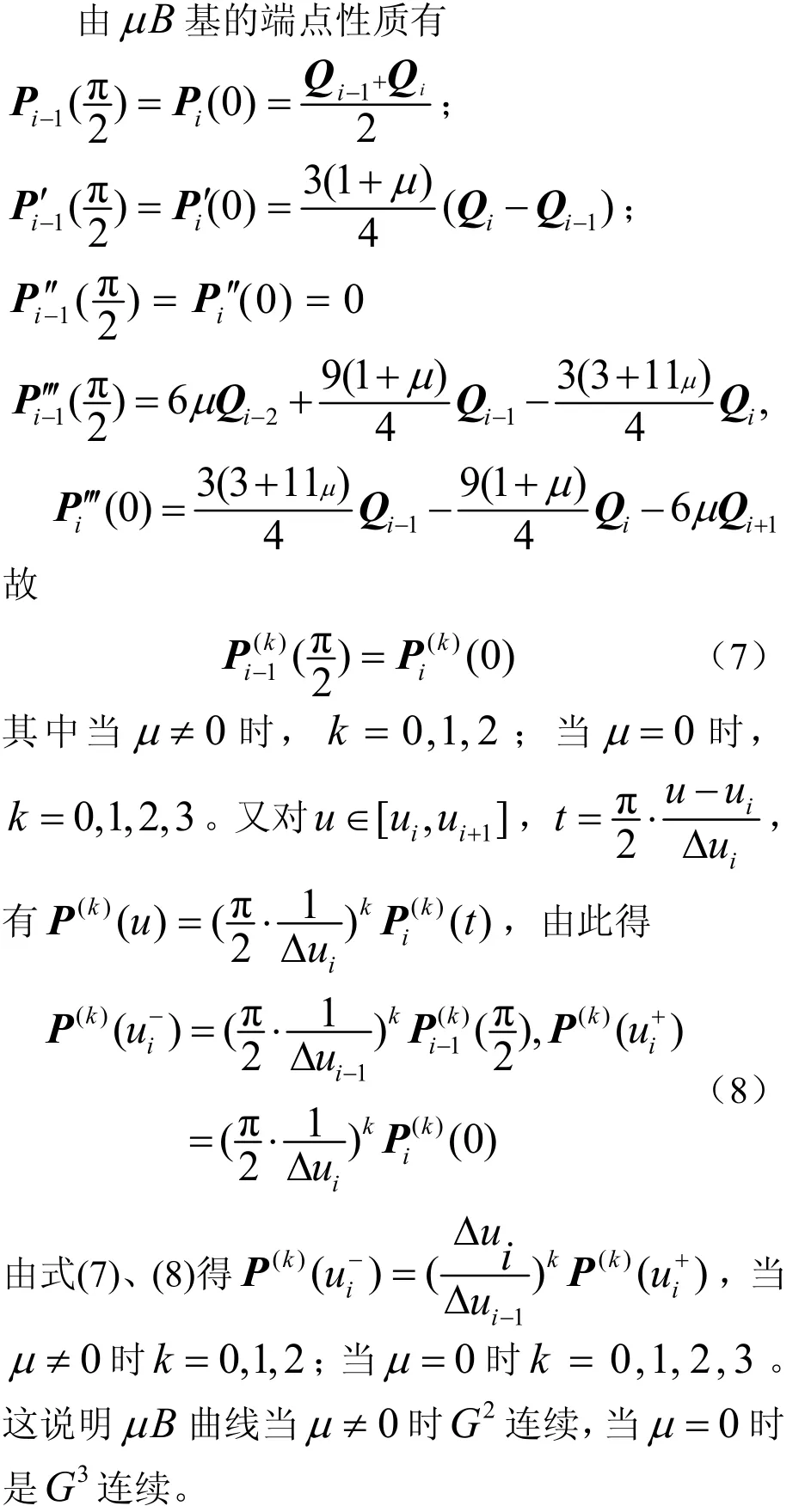
2.3 曲线的逼近性

图4 取不同参数值时的Bμ-曲线段

[1]朱仁芝, 程漠嵩. 拟合任意空间曲面的三角函数方法[J]. 计算机辅助设计与图形学学报, 1996, 8(2)：108-114.

[2]Han Xuli. Quadratic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2002, 19(7)：479-502.

[3]Han Xuli. Cubic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2004, 21(6)：535-548.

[4]苏本跃. T-B样条曲线及其应用[J]. 大学数学, 2005,21(1)：87-90.

[5]吴晓勤, 韩旭里. 带参数的三次三角多项式样条曲线[J]. 计算机应用与软件, 2007, 24(4)：62-64.

[6]吴晓勤, 韩旭里, 罗善明.带形状参数的二次三角Bezier曲线[J]. 工程图学学报, 2008, 29(1)：82-87.

[7]王成伟. 带有参数的三次三角多项式样条曲线[J].北京服装学院学报, 2007, 28(3)：50-55.

Two kinds of trigonometric curves with shape parameters

Yan Lanlan1, Liang Jiongfeng2, Huang Tao1
( 1. College of Mathematics and Information Science, East China Institute of Technology, Fuzhou Jiangxi 344000, China;2. College of Civil and Environmental Engineering, East China Institute of Technology, Fuzhou Jiangxi 344000, China )

Two kinds of trigonometric curves with shape parameters are defined, they are trigonometric polynomial curves and cubic trigonometric spline curves. The former retains the main properties of the quadratic Bézier curve, and it is closer to the control polygon and can achieve higher order of continuity than the quadratic Bézier curve. The latter is similar to the quadratic B-spline curve, each piece of it is generated by three consecutive control points. For equidistant knots, the curves areC2continuous, and they areC3continuous under special conditions.

computer application; trigonometric basis; spline curve; shape parameter

TP 391

A

1003-0158(2012)01-0025-06

2008-12-23

严兰兰（1982-），女，湖北浠水人，讲师，硕士，主要研究方向为计算机辅助几何设计。