即时通信网络上的信息传播模型研究

文丨胡婕莹 张望成

（1 北京师范大学珠海分校，广东珠海 519000；2 四川大学，成都 610065）

即时通信是随着互联网的出现而兴起的新型通信手段，由于低成本、高效率、方便快捷，自诞生以来广受青睐。按易网国际《中国即时通信市场季度监测报告》的定义，即时通信（简称IM），是一个终端服务，允许两人或多人使用网络传递文字、档案、语音与视频交流，实现沟通信息实时收发及相关辅助信息即时更新。

由于网络世界的开放性和自由性，网络上人人都是传播者。每个使用即时通信工具的人都有固定的“好友”作为发布信息的“受众”。一旦有事发生，可以马上在小范围发布信息，同时以复制链接的方式向好友或群发布，使更多人知晓，因而对即时通信网络上信息传播模型的研究意义重大。

1 即时通信网络的特点分析

复杂网络理论是分析网络特性的有效手段。在分析网络特征时一般使用两个特征来衡量网络，即特征路径长度和聚合系数。前者是网络中所有节点对路径长度的平均值，后者是所有节点聚合系数的均值。在即时通信网络中节点A相邻节点的相邻节点很大可能和A相邻，现实中即A朋友的朋友很可能也是A的朋友。由于在即时通信网络中存在群的概念，很多人可以集中交流，一人可对多人信息传播。根据以上分析易知即时通信网络是一种小世界网络，即具有最短路径和高聚类系数的一种网络结构[1]。

根据以上特性我们提出了新的信息传播模型，不但考虑了各个节点的状态，而且加入了各状态间的转换概率。

2 即时通信网络上的信息传播模型

在病毒传播模型SIR[2]中，节点分三种：S（Susceptible）易染状态、I（Infected）感染状态、R（Removed）免疫状态。1991年ANDERSON和KEPHART又增加了潜伏期状态E（Exposed），提出SEIR模型[3]。在研究了即时通信网络上的信息传播特点后，我们提出IM-SEIR模型。为描述方便假设有信息A在即时通信网络上传播，S表示节点还没收到A，E表示已收到但还没激活A，I表示节点浏览后接受（信任或转发）A，R表示拒绝A，情况如图1。

S→E：A传到节点后，节点由S转换为E，此时信息未被激活，α表示接受到A的概率。E→I：节点浏览并信任或转发了A，概率为β。E→R：节点虽浏览但并未相信也没将A传给其他节点，概率为ε。I→R：节点由信任变为不信任A，概率为γ。S→R：节点被阻止收到A，概率为δ。R→I：节点由不信任变为信任A或把A传给其他节点。

图1

3 即时通信网络上信息传播模拟

3.1 模拟假设 笔者利用IM-SEIR模型模拟关键因素，通过改变参数取值分析其对信息传播的影响。假设用户数量N=1*108初始态S(0)=1*108、E(0)=0、I(0)=0、R(0)=0信息尚开始未传播。且认为在有限时间段内，用户数量相对稳定。

3.2 正面信息自由传播 假设此时系统中有一正面信息可自由传播，仿真使用参数α=0.01，δ=0（服务商没有屏蔽信息），β=0.08，ε=0.01，γ=0.001，θ=0.003，结果如图2。正面信息在0-200时间内迅速被80%左右的用户接受，约20%的用户最终不接受信息，和现实拟合。

图2

3.3 负面信息受限传播

3.3.1 参数δ对信息传播的影响 图2中R状态的节点0-600时间内缓慢增长到稳定状态，I在0-250内迅速增长到最大值；图3中R在0-100内迅速增长到最大值后稳定，I在0-600内缓慢达到最大值并稳定。比较可知平衡时I和R的节点数量基本无变化。

假设此时有一负面信息，δ代表服务商对信息限制的概率。分析可知，服务商的阻止只能在一定程度上延缓用户接受信息的时间，不能改变最终接受信息的用户量。

3.3.2 参数β、θ对信息传播的影响 β、θ代表用户对不良信息的判断能力，假设有一不良信息传播，β为0.03，θ为0.001，由图4可知I在0-250时迅速达到最大值后稍降到平衡，R逐渐上升到平衡，和图2相比I下降，R上升。可见用户对不良信息的识别能力直接影响到信息的传播范围。

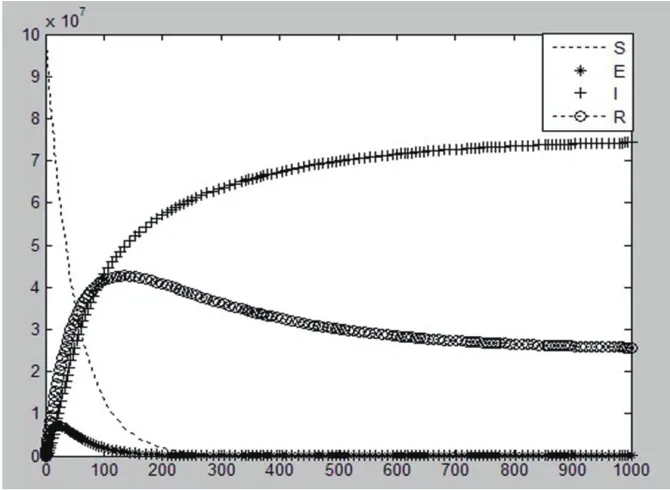
图3

4 结束语

即时通信网络上信息的传播受多种因素影响，笔者提出的IM-SEG模型，通过仿真实验进行分析，提出应对不良信息传播的策略，对加强信息的监管控制有很高的实用价值。

图4

[1]汪小帆，李翔，陈关荣，等. 复杂网络理论及其应用. 北京：清华大学出版社，2006：162-163.

[2]KEPHART J O, WHITE S R.Directed-graph epidemic-cological models of computer viruses[c], //Proceeding 1991 IEEE Computer Society Symposium on Research in Security and Privacy. [S.1.]:[S.n.], 1991: 343-359.

[3]ANDERSON R M, MAY R M.Infectious diseases of humans dynamics and control[M]. Oxford: Oxford University Press, 199l: 15-21.