无刷直流电机离散滑模观测器直接转矩控制

，，

（天津理工大学 天津市复杂系统控制理论及应用重点实验室，天津 300384）

无刷直流电机传统脉宽调制电流控制会产生较大的换相电磁转矩脉动，且出现非理想反电势时，还会产生原理性电磁转矩脉动。为抑制电磁转矩脉动，可将直接转矩控制思想引入到无刷直流电机的控制中。文献［1］提出一种转矩直接控制方法，将转矩参考值和反馈值输入到转矩控制器之后经过计算得到所要求的占空比，来控制相应的开关管。文献［2］将基本直接自控制引入无刷直流电机。文献［3］将直接转矩控制和模糊控制相结合应用于无刷直流电机控制系统。

由于无刷直流电机定子磁链的观测和给定非常困难，电磁转矩的估算精度不高，本文采用离散滑模观测器获取无刷直流电机反电势，进而完成电磁转矩的估算，然后由转矩滞环的输出和磁极位置来选择电压空间矢量，从而实现无刷直流电机直接转矩控制。

1 产生电磁转矩脉动的原因

三相Y接无刷直流电机的状态方程为

式中：u为相电压；i为相电流；e为反电势；R为相电阻；L为相电感。

假设无刷直流电机脉宽调制电流控制采用两相导通6状态电子换相方式，脉宽调制为H＿on－L＿pwm。理论上，无刷直流电机的反电势为梯形波，用同相位的方波电流脉冲驱动，就能得到平滑的电磁转矩。

为减少电流传感器的数目，通常采用检测母线电流的方法获得定子电枢绕组反馈电流。该方法在PWM＿on的中间时刻采样母线电流，但是在占空比较小的时候准确性不易保证。此外，电流换相时，母线中的电流为开通的换相相电流，该电流从零开始增长，不能真实反映此时的电磁转矩，这也会造成电磁转矩脉动。一种较新颖的定子电枢绕组电流检测方案可克服以上缺点［4］。该检测单元由2个匝数相等的线圈、磁环和线性霍耳元件构成，但这种定子电枢绕组电流检测方案要求主电路由分立元件构成。即使反馈电流可准确反映电机的电磁转矩，当出现非理想反电势时，电流调节器仍然通过脉宽调制保持方波定子电枢绕组电流，这样就会产生原理性电磁转矩脉动。

2 离散滑模观测器及电磁转矩的估算

滑模动态满足匹配条件时与系统的参数摄动和外界扰动完全无关，这就使得处于滑模运动的系统具有很好的鲁棒性［5］。S.Z.Sarpturk等人提出了离散系统的滑模到达条件和稳定条件［6］

下面对无刷直流电机滑模观测器的这2个条件进行证明。

由于无刷直流电机常无中性点引出线，三相定子电枢绕组的相电压无法直接测量得到。而经变换

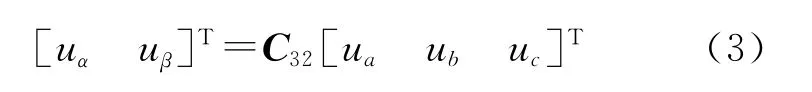
其中

就可以由线电压得出

考虑参数变化后，由式（1）可得无刷直流电机在αβ坐标系下的电压平衡状态方程

其中

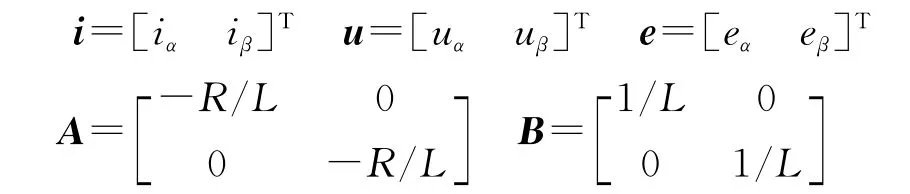
采用零阶保持器法将状态方程离散化

定义滑模面

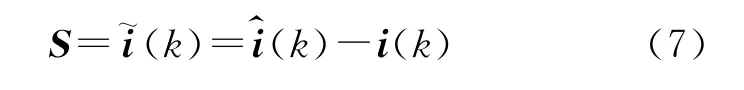
滑模观测器方程为

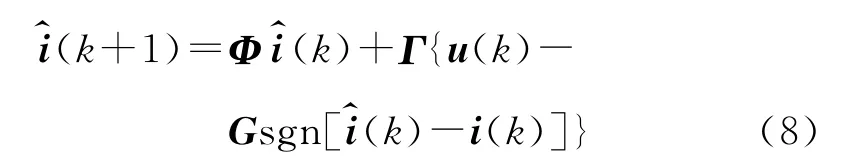
式中：G＝gI，g为增益，I为单位矩阵。

以α轴为例证明到达条件和稳定条件。

1）到达条件。由式（6）～式（8）得

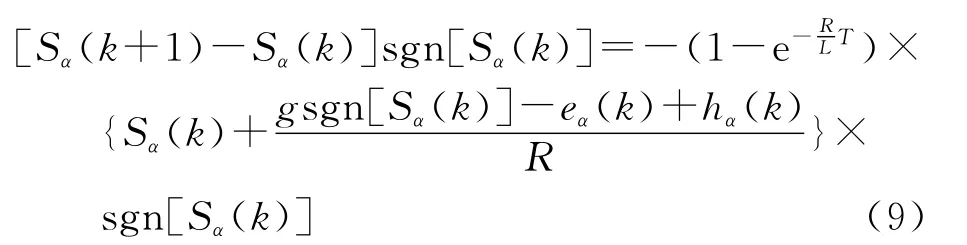
若g≥max｜eα（k）－hα（k）｜，则满足到达条件。

2）稳定条件。由式（6）～式（8）得

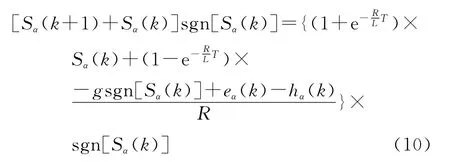
则满足稳定条件。

由式（6）～式（8）得

由式（6）～式（8）得

由式（11）、式（12）可知，当T很小时，Sα（k＋1）趋于零。

αβ坐标系下无刷直流电机的电磁转矩为

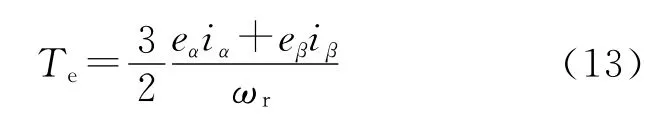
式中：ωr为转子机械转速。

3 直接转矩控制的原理

3.1 电压空间矢量的选取及定子磁链的轨迹

无刷直流电机控制系统主电路拓扑如图1所示。

图1 主电路Fig.1 Main circuit

逆变器的通电状态可用一组二进制序列表示（S1S2S3S4S5S6），Si＝0（i＝0，1，…，6）代表功率器件关闭，Si＝1代表功率器件导通。

假设无刷直流电机非导通相反电势为零，定义电压空间矢量

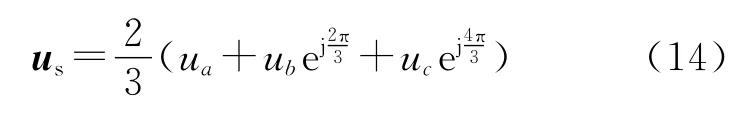
选取6个电压空间矢量，如表1所示。

表1 电压空间矢量Tab.1 Voltage space vectors

这6个电压空间矢量将空间分为Ⅰ～Ⅵ共6个扇区，每一扇区占60°（电角度）。空间分布见图2。

图2 电压空间矢量的分布Fig.2 Voltage space vectors distribution

例如，若定子磁链位于Ⅰ扇区，施加电压空间矢量U2，则定子磁链沿六边形轨迹逆时针方向旋转。施加电压空间矢量U5，则定子磁链沿六边形轨迹顺时针方向旋转。事实上，受非导通相反电势的影响，定子磁链并不能完全沿六边形轨迹旋转，而是会出现跳变的花瓣形。由于无刷直流电机霍耳磁极位置传感器有6种输出信号，而且转子磁链和定子磁链保持一定的夹角，所以可用这6种信号选择电压空间矢量。

3.2 电磁转矩的控制

由电机统一理论知，电机的电磁转矩

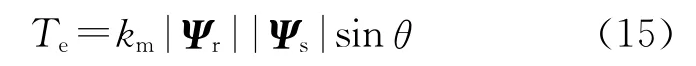
式中：km为转矩系数；｜Ψr｜，｜Ψs｜分别为转子磁链幅值和定子磁链幅值；θ为定子磁链和转子磁链之间的夹角。

设无刷直流电机六边形磁链轨迹的内接圆半径为r，运动速度为v，转子磁链沿逆时针方向旋转，定子磁链位于扇区Ⅰ，初始位置在A点。

定子磁链幅值

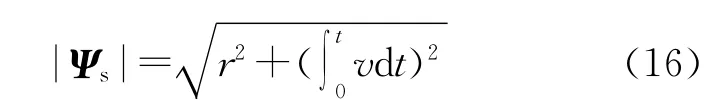
当定子磁链运动到B点时，定子磁链幅值变化率的绝对值最大。由式（16）可得

定子磁链和转子磁链之间夹角的正弦值为

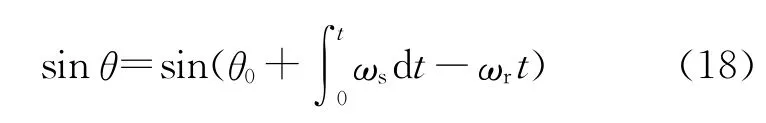
式中：θ0为定子磁链与转子磁链夹角的初始值；ωs，ωr分别为定子磁链和转子磁链的旋转速度。

定子磁链走过的角度为

当定子磁链运动到B点时，θ′s的绝对值最小。由式（19）可得

可见，电磁转矩的变化主要取决于定子磁链与转子磁链的夹角。控制定子磁链与转子磁链的夹角可以实现对无刷直流电机电磁转矩的控制。

无刷直流电机直接转矩控制系统的结构，见图3。转速调节器输出为滞环比较器的给定，此给定与电磁转矩估算值的差值经滞环比较器后，再结合霍耳磁极位置传感器输出信号选择相应的电压空间矢量，从而实现无刷直流电机直接转矩控制。

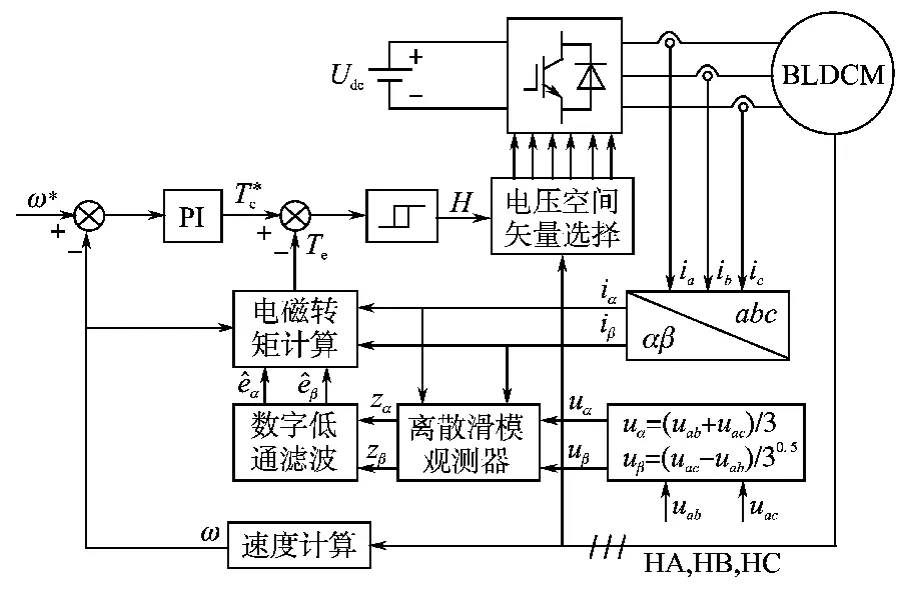
图3 无刷直流电机直接转矩控制系统的结构Fig.3 Scheme of direct torque control for BLDCM

低速换相时，关闭的换相相电流的衰减比开通的换相相电流的增长慢。此时，直接转矩控制可通过选择相应的电压空间矢量对开通的换相相电流斩波，从而保持非换相相电流恒定，抑制电流换相电磁转矩脉动。高速时，关闭的换相相电流的衰减比开通的换相相电流的增长快。此时，直接转矩控制失去电流换相电磁转矩脉动抑制能力。

4 仿真结果及结论

为验证上述分析的正确性，在Simulink中搭建无刷直流电机直接转矩控制仿真模型。无刷直流电机参数如下：额定功率1.1kW，额定电压170V，额定转速3 000r／min，定子电阻0.832Ω，定子电感1.4mH，极对数4。

仿真结果如图4所示。图4b为反电势实际值与估算值的比较。离散滑模观测器算法简单，参数鲁棒性强，可有效检测无刷直流电机反电势，但低通滤波器引起的反电势相位滞后会影响电磁转矩的估算精度。图4d为低速时的电磁转矩。与脉宽调制电流控制相比，直接转矩控制能有效抑制非理想反电势和低速换相电磁转矩脉动。由图4f可知，为抑制非理想反电势电磁转矩脉动，定子电流不再是方波。

离散滑模观测器算法简单，参数鲁棒性强，而且适合于计算机控制，可以为无刷直流电机直接转矩控制系统提供电磁转矩反馈。根据电磁转矩滞环比较器的输出和霍耳磁极位置传感器的输出选择电压空间矢量，实现无刷直流电机的直接转矩控制。该方法简单，可以有效抑制非理想反电势和低速换相转矩脉动。在电磁转矩的估算中，采用低通滤波器对高频信号Z滤波，由此引起的反电势相位滞后将会影响电磁转矩的估算精度。

［1］张磊，瞿文龙，陆海峰，等.非理想反电势无刷直流电机转矩直接控制方法［J］.清华大学学报：自然科学版，2007，47（10）：1570－1573.

［2］高瑾，胡育文，黄文新，等.六边形磁链轨迹的无刷直流电机直接自控制［J］.中国电机工程学报，2007，27（15）：64－69.

［3］王晓远，田亮，冯华.无刷直流电机直接转矩模糊控制研究［J］.中国电机工程学报，2006，26（15）：134－138.

［4］逄格民，李铁才.无刷直流电动机新型电流检测方法［J］.微电机，2010，43（1）：91－93.

［5］Caminhas W M，Takahashi R H C，Peres P L D，etal.Discrete－time Sliding Modes Observers for Induction Motors［C］∥Proceedings of the 1996IEEE International Conference on Control Applications.Dearborn，America：IEEE，1996：314－319.

［6］刘金琨.滑模变结构控制MATLAB仿真［M］.北京：清华大学出版社，2005.