基于傅立叶分析的三相SPWM逆变器死区效应与补偿研究
2012-09-22张佩炯苏宏升
张佩炯,苏宏升
(兰州交通大学自动化与电气工程学院,甘肃兰州730070)
1 引言
对于SPWM全桥式逆变器,因所用开关管固有开关管存储时间的影响,开通时间往往小于关断时间,因此很容易发生同桥臂两只开关管同时导通的短路故障。为了保证同桥臂上的一只开关管可靠关断后,另一只开关管才能开通,通常要设置死区时滞Δt[1]。设置死区的方式有双边对称设置和单边不对称设置两种方式。前者,提前Δt/2关断,延滞 Δt/2 开通;后者,按时关断,延滞 Δt开通[2]。本文主要讨论了后一种设置对逆变器输出波形的影响,最后通过仿真和实验验证了该方法的有效性。
2 三相桥式PWM逆变电路分析
三相桥式PWM逆变电路如图1所示,它采用双极性控制方式。U、V和W三相的PWM控制通常公用一个三角波载波Uc,三相的调制信号urU、urV和urW依次相差120°。U、V和W各相功率开关器件的控制规律相同,现以U相为例来说明。当urU>Uc时,给上桥臂V1以导通信号,给下桥臂V4以关断信号,则U相相对于直流电源假想中点N′输出电压 uUN′=Ud/2。当 urU<Uc时,给 V4以导通信号,给V1以关断信号,则 uUN′=-Ud/2。V1和 V4的驱动信号始终是互补的。当给V1(V4)加导通信号时,可能是V1(V4)导通,也可能是二极管VD1(VD4)续流导通。当然,V相和W相的控制方式和U相相同。电路的波形如图 2 所示。可以看出 uUN′、uVN′和 uWN′的PWM波形都只有±Ud/2两种电平。图中的线电压波形uUV的波形可由uUN′-uVN′得出。可以看出,当臂1和6导通时,uUV=Ud,当臂3和4导通时,u-UV=-Ud,当臂 1 和 3 或臂 4 和 6 导通时,uUV=0。因此逆变器的输出线电压PWM波由±Ud和0三种电平构成。
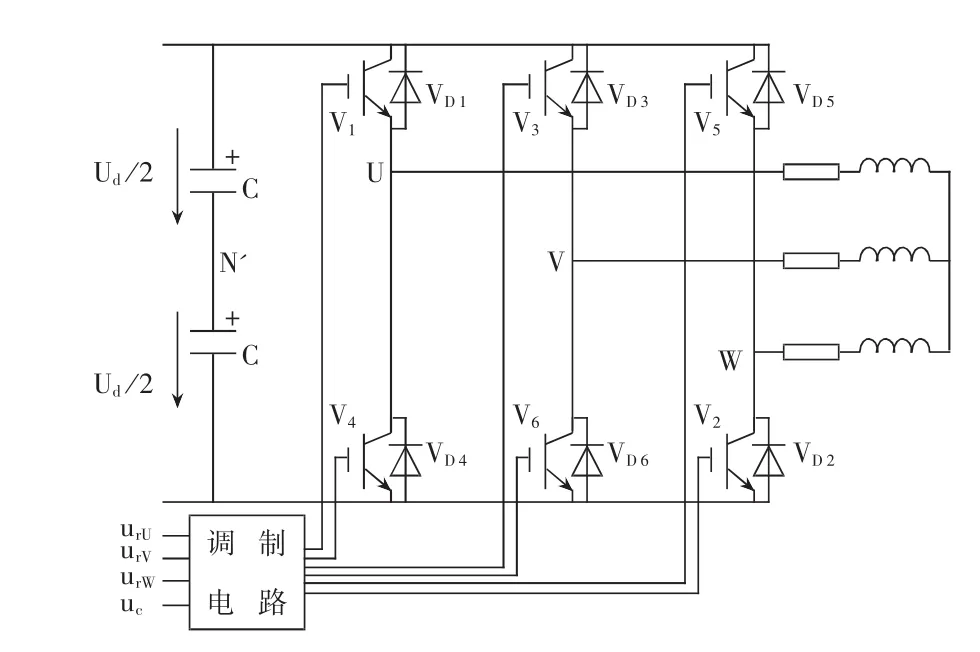
图1 三相桥式PWM型逆变电路
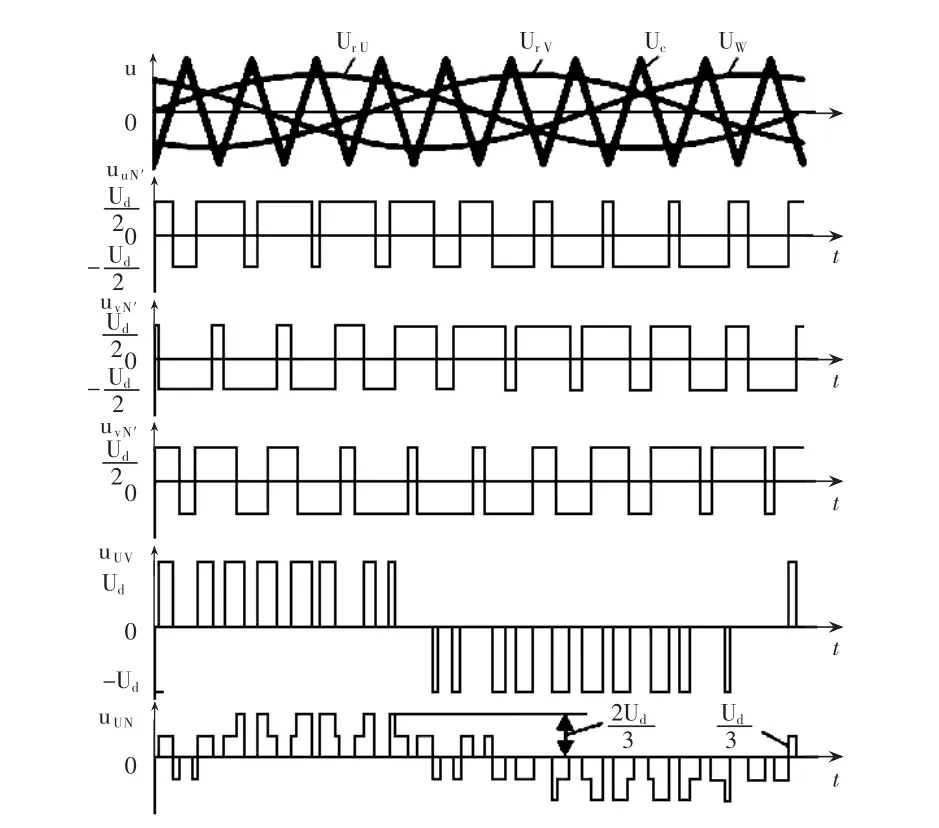
图2 三相桥式PWM型逆变电路波形
通过以上分析可以看出,方波逆变电路输出的基波电压仅取决于直流电压Ud的大小,因而只能通过调节Ud来控制大小,此外因在一个电压输出周期内各开关器件只通断一次,故其谐波含量也较大。当前广泛应用的SPWM逆变电路通常采用IGBT作为开关器件,在一个电压输出周期中,对各开器件进行多次通、断控制,这样既可调节输出电压的大小和频率,又可降低各次谐波分量的影响。
同样,当负载为感性时,如电动机,负载电流不能突变,这样也可以使逆变器输出的电流波形更接近于正弦波,使其运行更加平稳,也减小了损耗,提高了效率。
对SPWM逆变电路分析时,应分同步和非同步两种调制方式情况来分析。在非同步SPWM调制时,一个调制波周期内所含的各脉冲模式不具备重复性,因而无法以调制波的角频率ωs为基准,用傅立叶级数把它分解为ωs倍数的谐波。此时以载波角频率ωc为基准,考察其边频带波分布情况的方法较合适。
3 三相逆变器的死区效应
3.1 逆变器死区产生的原因
实际开关器件的开关都需要一定的时间才能完成,常用于逆变桥的IGBT开通和关断是由栅极和发射极间电压UGE决定的,当为正且大于开启电压 UGE(th)时,MOSFET 内形成沟道,并为晶体管提供基极电流进而使IGBT导通;当栅极与发射极间施加反向电压或不加信号时,MOSFET内的沟道消失,晶体管的基极电流被切断,使得IGBT关断。如图3所示为IGBT的开关过程图,从图3可以看出:在IGBT打开时,栅射极驱动电压UGE从其幅值10%到集电极电流ICN上升到其90%幅值时需要ton时间开通;在IGBT关闭时,栅射极驱动电压UGE从其幅值90%到集电极电流ICN下降到其10%幅值需要toff时间关断。ton和toff通常称为IGBT的开通和关断时间。
180°导通电压源型逆变器,换流是在同一桥臂上、下两个开关器件之间完成,其驱动信号采用互补的PWM信号,由于IGBT的开和关需要一定的时间,而且通常toff>ton,因此就有可能出现上、下两个开关器件同时导通的现象(即一个还未完全关闭而另一个就已打开)。当同一相桥臂上、下两个开关器件同时导通时,就会导致直流侧电源短路。为了防止这一现象的出现,通常在逆变器同一桥臂上、下两个开关器件导通之间加入一定的时间间隔。即采取“先断后通”的方法,先给要关断的开关器件输送关断信号,然后留一定的时间裕量,待其完全关闭后,再给要导通的器件发出开通信号,通常把这些“时间裕量”称为逆变器的死区时间,通常用td来表示。死区时间的长短要视器件的开关速度而定,器件的开关速度越快,所留的死区时间就可以越短。在常用的IGBT三相逆变桥中,通常死区时间都要大于4μs。死区时间给逆变系统带来的一些负面影响称为死区效应。
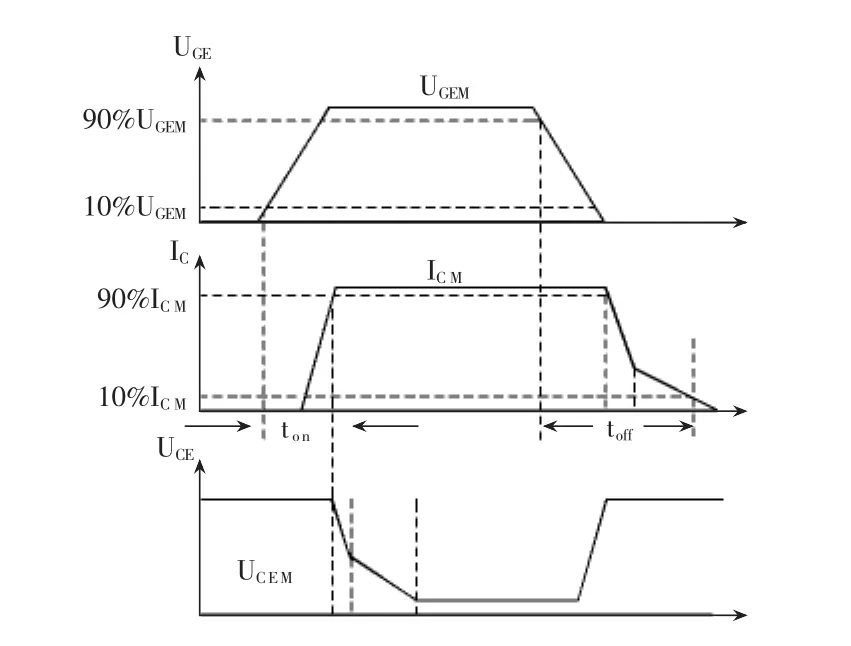
图3 IGBT开关过程
死区设置方式有两种:一种是提前td/2关断,延滞td/2开通,称为双边对称设置;另一种是单边不对称设置,即只让一个开关器件延滞td开通或提前td关断。
3.2 死区效应分析
用三相逆变器中的一相来分析死区效应,图4所示为三相逆变器A相结构图,图示电流方向假定为正。
如图5所示为死区双边对称设置时逆变器A相输出电压波形分析,图6为死区半边不对称设置时(每个功率开关器件正常关,延滞td开通)逆变器A相输出电压波形分析。两图中(a)是调制过程,其中USA是A相的调制波,UC是三角载波,IA是相线电流;(b)和(C)是调制出的桥臂上、下开关器件的理想驱动信号;(d)是A相理想的电压波形;(e)和(f)是加入死区后的 A 相桥臂上、下开关器件的驱动信号;(g)是逆变器空载时的电压波形。空载时二极管不续流,因此在死区时间内上、下功率开关器件都不导通,此时输出电压为0;(g)为逆变器拖动感性负载时A相电压波形图。当逆变器拖动感性负载时,在死区时间内,桥臂上、下开关器件同时关闭后,电流通过二极管续流,这就会给输出电波带来误差波。具体是哪一个二极管续流这与电流的方向有关。当IA<0时,电路通过VD1续流,此时输出电压为 Ud/2,当 IA>0 时,电路通过VD2续流,此时输出电压为-Ud/2;(i)为带死区时间时逆变器A相实际输出电压与逆变器理想输出电压之间的偏差。

图4 三相逆变器A相结构
从图5和6中可以看出,死区设置方式不同时由死区时间引起的误差波也不一样。死区双边对称设置时,同一桥臂上、下功率开关器件无论哪个开关一次就会产生一个误差波,此误差波为电压值为Ud,时间间隔为td/2的矩形波,设载波比为N,那么在一个调制波周期内就会有2N个矩形误差波。死区单边不对称设置时,同一桥臂上、下功率开关器件各开关一次才会产生一个矩形误差波,此时的误差波电压值也为Ud,不过时间间隔变为td,此时在一个调制波周期内有N个矩形误差波。从图中还可以看出,当IA<0时,死区双边对称设置方式的逆变器A相实际输出波形比理想的电压波形多出[(td/2)N] Ud,死区单边不对称设置方式多出[td(N/2)] Ud;当 IA>0 时,死区双边对称设置方式的逆变器A相实际输出波形比理想的电压波形少了[(td/2)N] Ud,死区单边不对称设置方式少了[td(N /2)] Ud。

图5 死区双边对称设置时的波形图

图6 死区单边不对称设置时的波形图
电压型逆变器误差波产生是死区时间内二极管续流引起了电压突变所引起。假如逆变器拖动电动机负载,在死区时间内,需要通过二极管续流反馈无功功率,这样就产生了误差波。当开关器件G1导通时,A点电位为Ud/2,当G2导通时,A点电位为-Ud/2,理想情况下,G1和G2导通电角度各为180°。但当IA>0,在死区时间内都是通过VD2续流,此时A点电位就为-Ud/2,若理想的逆变器此时电位应为 Ud/2,这时就会少 tdUd;同理,当 IA<0,在死区时间内都是通过VD1续流,此时A点电位为Ud/2,理想的逆变器电位为-Ud/2,多出 tdUd,因此误差波与电流的极性有很关。
图7为对死区效应的初步分析,图中的(a)为理想的调制过程,USA为理想的调制信号,iA为理想的负载电流;(b)为电压误差波;(c)为实际电压波形;(d)为实际电流波形。因死区时间的存在,实际输出的电压波形应为理想的电压波形加上因死区时间产生的电压误差波。电压误差波的极性与实际电流波的极性相同,与理想电压波之间有φ相位差,从图中可以看出电流过零点后,因误差波的极性也随之发生了改变,这样就会使逆变器在电流过零点时的实际输出电压出现突变,但当负载是感性时,电流无法突变,而且系统中肯定会产生一个反作用来阻止电压突变。
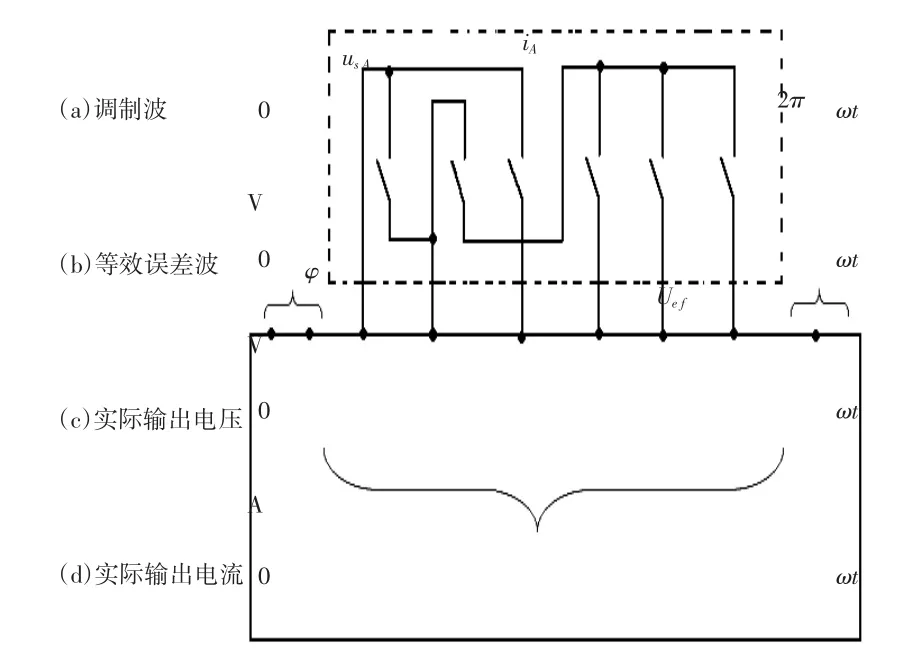
图7 加入死区后逆变器输出波形分析
4 死区效应的傅立叶分析
设 A 相控制信号为 USA=msin(ωst),那么在 θ1和 θ2处,USA=UC,这样可得到:

A 相对于“o”的电压


式中:

根据以上各式可求得:

把上式代入式(3)可得:

为了进一步对逆变器输出的谐波分量分析,利用贝塞尔函数对上式进一步分解,贝塞尔函数的积分表达式为:

对于贝塞尔函数有下列等式成立[3]:

式(6)的第二项为谐波成分,把它记为Aao,利用公式(8)可得:
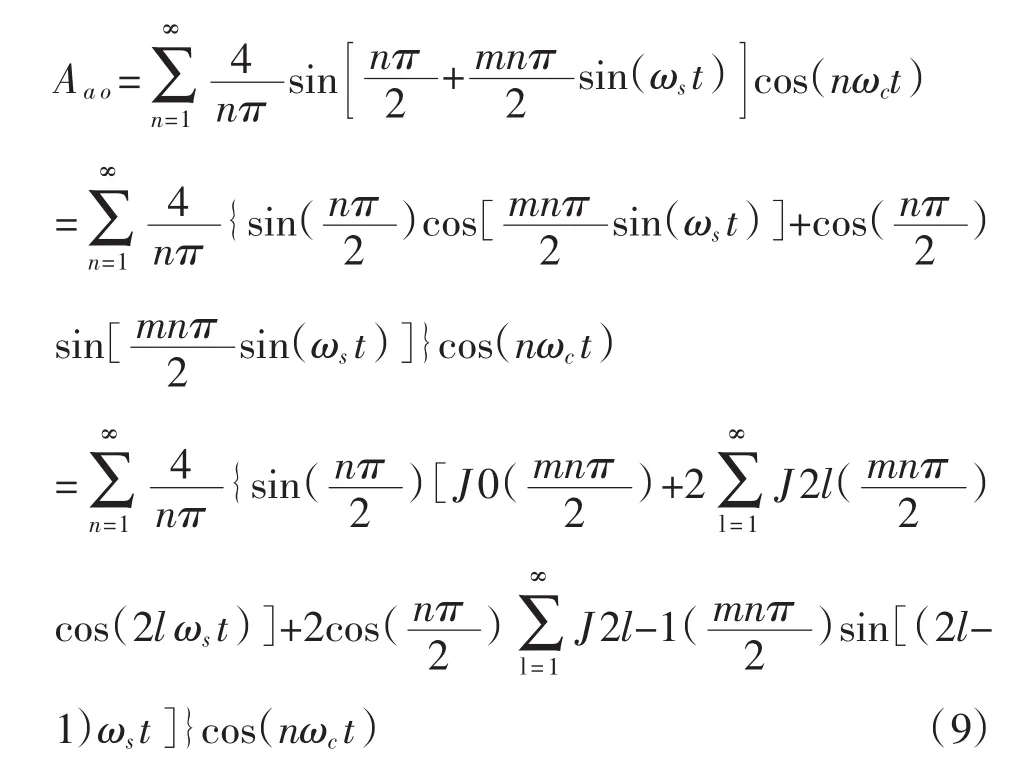
负载的线电压为:
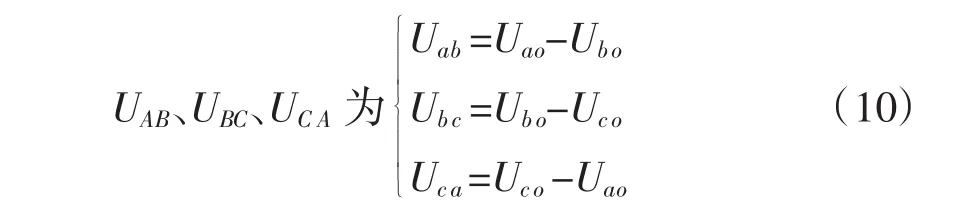
再根据式(6)和式(10)可得到逆变器的线电压,基波分量为:
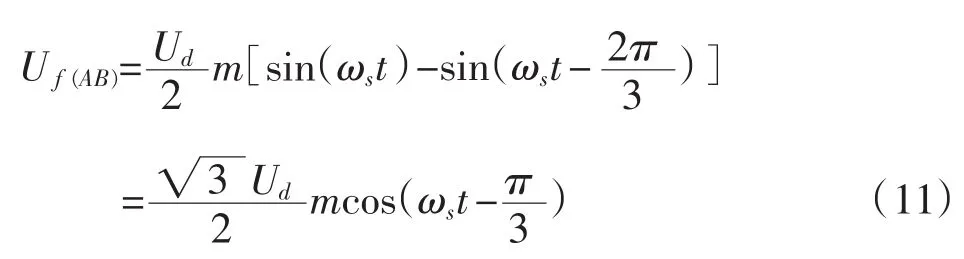
谐波分量分别用两种情况来讨论:
①当n为奇数时

式中
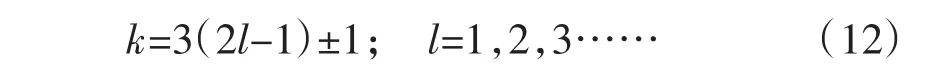
②当n为偶数时
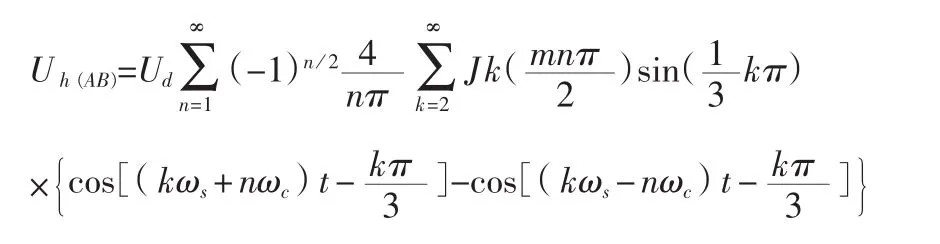
式中
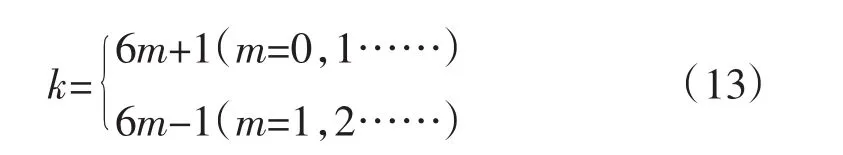
为了分析方便,取 φ=π/2,那么以图 7(b)所示选取坐标系,将矩形电压误差波用傅立叶级数展开:由图7可知误差波的基波幅值为谐波幅值为(n=2k+1,k=1,2……)。
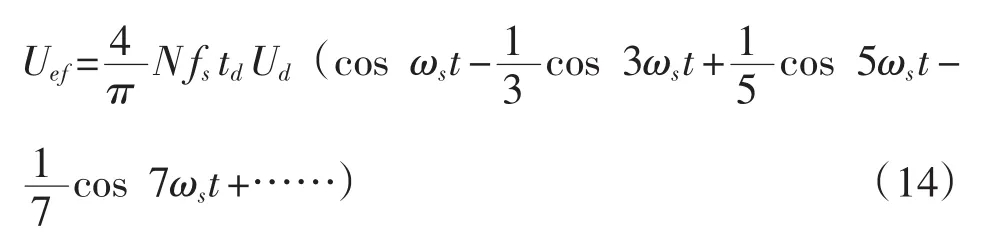
由(9)式可知,SPWM理想逆变器A点相对于假想电压中点的傅立叶表达式:
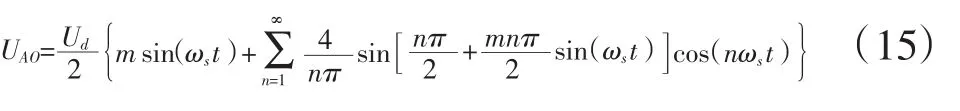
将式(14)和(15)相加可得SPWM逆变器实际输出电压波形为:

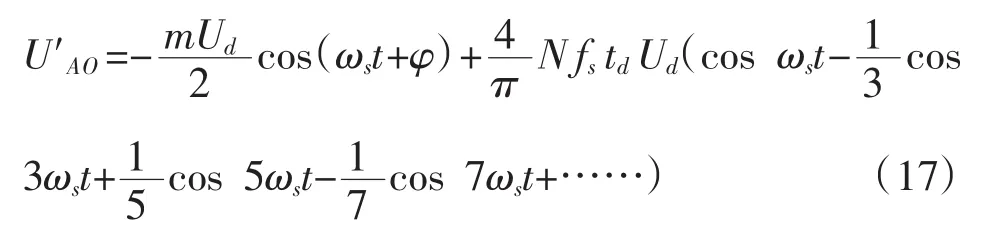
同理可得到B相对于假想电压中点电压基波的傅立叶表达式:

将(17)式和(18)式相减得到线电压的基波分量为:

其中

5 死区补偿的分析
常用的死区补偿方法目前没有统一的分类,在国内,首先提出了根据反馈量的不同将死区补偿方法分为电流反馈型和电压反馈型补偿方法[7]。根据各种补偿方法的特点将其分为三类:直接补偿法、基于无效器件原理的补偿方法和电流预测控制方法[8]。其后又将补偿方法分为:矢量补偿法、脉冲补偿法和PI调节器自适应补偿法[9]。文献中还提到死区解耦控制法、反馈校正补偿死区法、死区电压矢量调制法、改变开关频率补偿死区法、直接检测电流过零点补偿法、利用旋转变换坐标系补偿法、预测电流过零点补偿法、基于自适应模糊逻辑补偿法等[10]。
不同的人分析的角度不同,分类法随之也不相同,但就研究现状来说,比较合理的分类方法分为反馈型和非反馈型。反馈型死区补偿方法是要测量某些反馈量如电流和电压,然后根据这些反馈量采用不同的算法来改变控制信号或驱动信号对死区加以补偿,如果测量精度高,算法合理,补偿效果自然就好。非反馈型死区补偿方法在应用时不需要反馈量,一般是根据事先测得的电机参数确定电机模型,然后再计算出功率因数角,根据功率因数角对驱动信号加以补偿[5]。
下面对比较常见的死区补偿方法电流反馈型补偿法和电压反馈型补偿法加以讨论。
电流反馈型补偿电路如图8所示,其原理是:通过检测逆变器的三相输出电流,得到误差方波信号加到调制波上,通过检测A相电流iA后得到误差方波电压Ui,再将其转化成正弦信号波形Ui∠φ与A相调制波Us相加,然后调制生成PWM波UAO+Ucom,并加入死区后生成IGBT的驱动控制(U′AO+Ucom)。

图8 电流反馈型补偿电路
由死区效应分析可知,偏差方波电压与电流的极性有非常明确的对应关系。方波的幅值可以通过IGBT在一个周期内的开关次数事先加以计算,因此只要能够适时检测出三相电流的极性,则不难得到合适的补偿电压。如果所检测的定子电流无差并且无时间上的滞后,则理论上讲可以得到令人满意的补偿效果,但是实际系统中,电流的极性往往难以准确确定,其原因是:一是电流检测精度的问题,因受死区时间及电流幅值和频率的影响,会使逆变器输出电流在零区域产生交越失真[4],因而电流过零点一般存在一定程度的模糊性,因此电流过零点就更加难以确定;二是必要的电流滤波环节也加剧了电流过零点检测的难度,首先是电机定子电流中含有丰富的高频噪音,其次检测信号滤波环节引起检测信号的滞后,它们都会对死区时间的补偿效果有一定的影响[12]。
电压反馈补偿原理如图9所示,该方法首先检测出系统逆变单元的实际输出电压,然后与指令电压比较,其差值作为补偿量迭加到指令电压上作为新指令。同样以A相为例对其补偿过程加以说明,在图9中先用检测变压器检测出PWM的A相输出电压,并将其倒相变成-U″AO,然后用-U″AO与给定的PWM脉宽调制信号相加得到补偿电压Ucom,将U′AO+Ucom加入死区后得到新的驱动控制(U′AO+Ucom)。
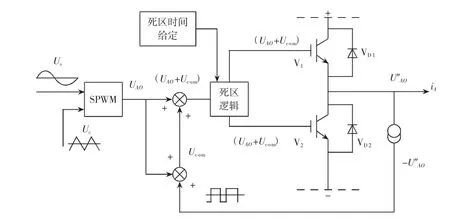
图9 电压反馈型补偿电路
电压反馈型死区时间补偿方案是一种直接的补偿方法,偏差电压通过直接检测得到而不是估计,并且对输出电压来讲具有准闭环控制的思想,因此原则上能够消除由环内的逆变单元所引起的任何输出电压和指令电压的误差(包括器件的开关死区时间),并且不受负载电流变化的影响,具有很好的补偿效果[15]。
6 Matlab仿真分析死区时间对SPWM逆变器的影响
为了验证仿真的可行性,用Matlab进行仿真,故搭建了仿真模型如图10所示。具体参数设置如下,直流电压为530V,三相负载中的有功为1kW,感性无功为500Var。
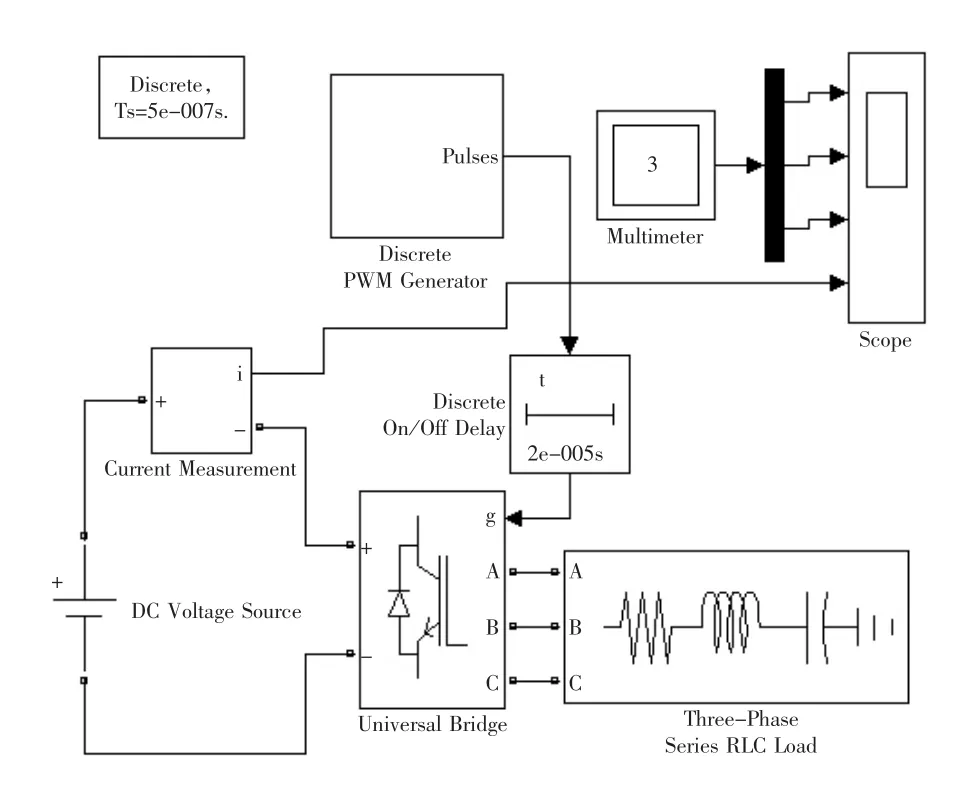
图10 死区时间对三相SPWM逆变器影响的仿真模型

图11 Ua n的波形
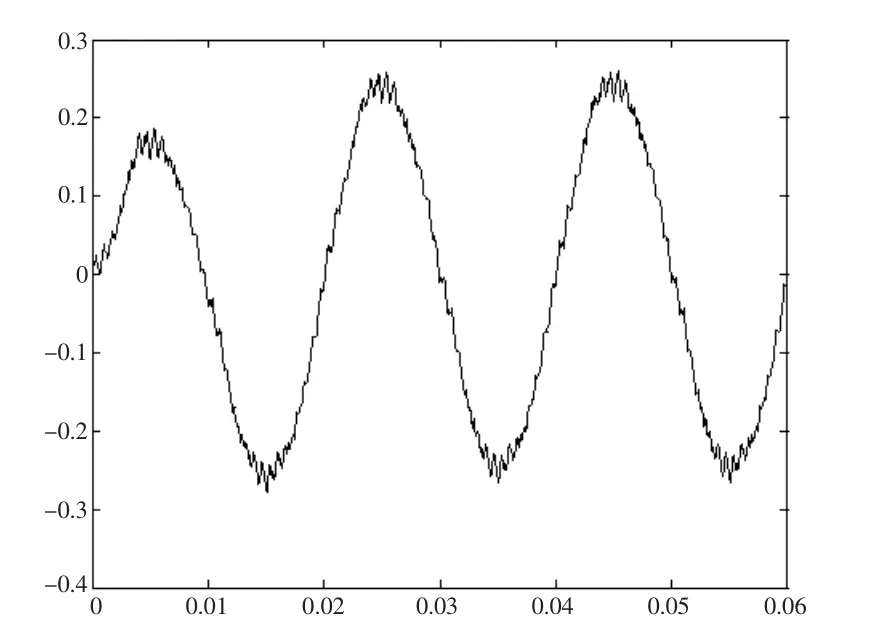
图12 ia的波形
在“Discrete PWM Generator”模块中,选中内部发生模式,并将调制深度m设为1,输出基波频率设为50Hz,载波频率设为基频的30倍,即1500Hz。将仿真时间设为0.06s,采样时间设为5×10-7s,并用“Discrete On/Off Delay”模块来进行死区时间的模拟。在此模块里选择上升沿滞后模式,将死区时间设为2×10-5s。
运行后可得仿真结果,交流相电压、相电流、线电压和直流电流波形如图11、12、13、14所示,此时输出电压的谐波分析如图15所示,输出电压的基波幅值为459V,输出电压的THD为35.26%,从波形分析可以看出,加入死区后出现较为明显的低次谐波。
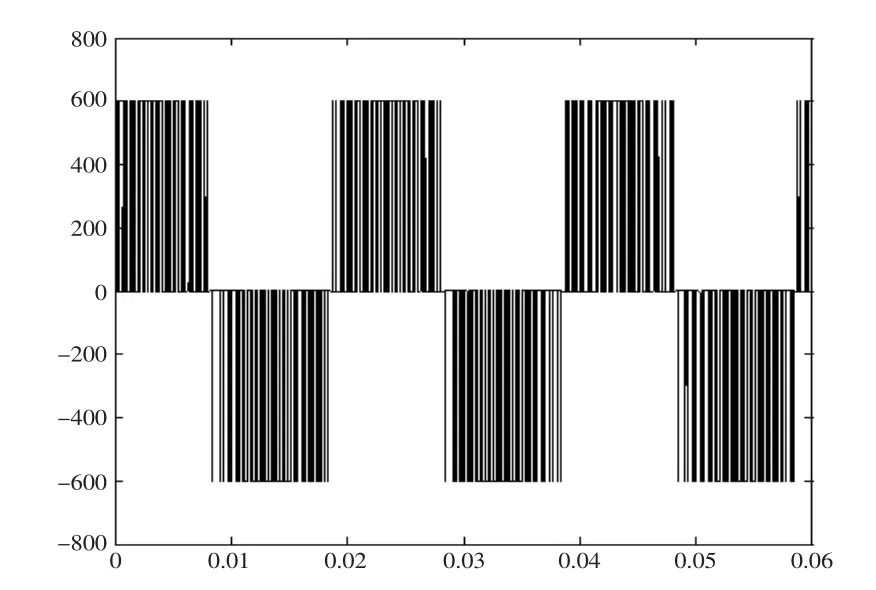
图13 Ua b的波形
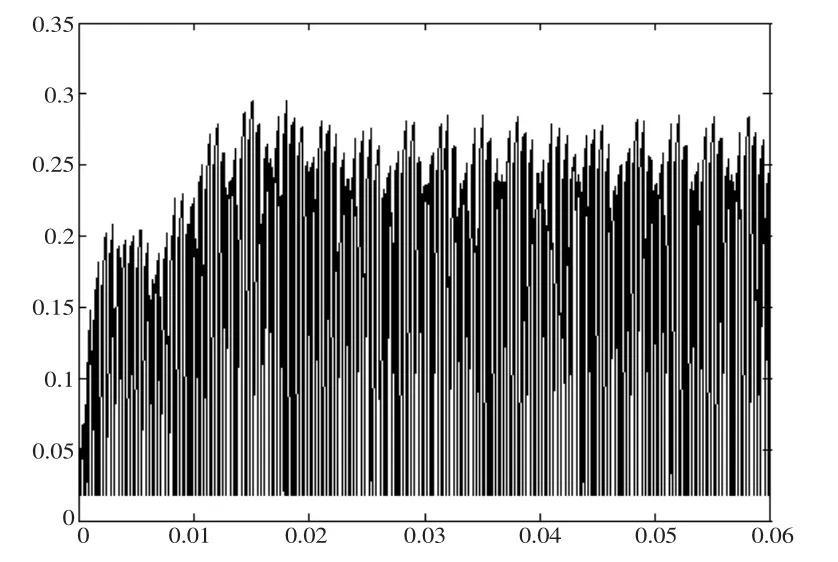
图14 id的波形
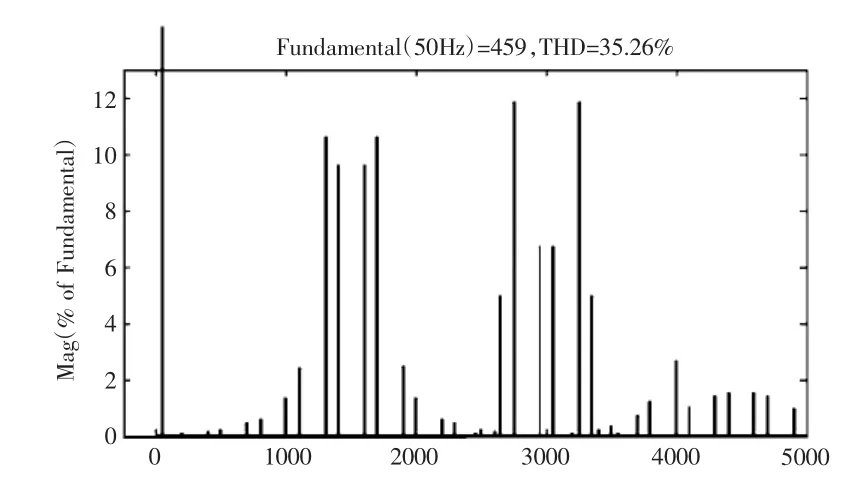
图15 有死区时三相SPWM逆变器输出电压的谐波分析
7 结论
利用傅里叶变换分析了三相SPWM逆变器设置死区时间对输出波形的影响。分析证明了因死区时间的存在以及二极管续流产生了使输出波形发生畸变的误差波,分析了死区补偿的方法,实验结果与理论分析相符,而且也证明本文提出的方法能使逆变器在设置死区时间的同时仍能使输出波形为正弦波。
[1] 王兆安,黄 俊.电力电子技术(第4版)[M] .北京:机械工业出版社,2009.
[2] 林渭勋.现代电力电子技术[M] .北京:机械工业出版社,2005.
[3] 白艳平,陆 平,薛亚奎.数学物理方法[M] .北京:北京理工大学出版社,2006.
[4] MURAI Y,WATANABE T,IWASAKI T.Waveform Distortion and Correction Circuit for PWM Inverters with Switching Lag-time[J] .IEEE Transaction,1985.
[5] 张燕宾.SPWM变频调速应用技术[M] .北京:机械工业出版社,2001.
[6] LEGGATE,KERKMAN.Pulse-based Dead-time Compensator for PWM Voltage Inverters[J] .IEEE Transactions on industrial electronics,1997,44(2):191-197.
[7] 余功军,钟彦儒,杨 耕.一种IGBT变频器死区时间的补偿策略[J] .电力电子技术,1997.
[8] 王 宏,于 泳,杨 明,等.PMSM伺服系统中的开关死区补偿技术[J] .电气传动,2004,26(Z1):138-141.
[9] 姜向龙,尹 泉,赵 金,等.基于DSP控制器的一种死区补偿策略[J] .电力电子技术,2005,39(4):44-46.
[10] 刘 亮,郑名高.一种补偿PWM逆变器死区效应的新方法[J] .电力电力技术,2005,39(6):123-125.
[11] 林 飞,杜 欣.电力电子应用技术的Matlab仿真[M] .北京:中国电力出版,2009.
[12] 王君艳.交流调速[M] .北京:高等教育出版社.2003.
[13] SUMMERS BETZ.Dead-time Issues in Predictive Current Control[C] .37th ISA Annual Meeting,2002,(3):2086-2093.
[14] 陈 硕,薛昭武.电压型 PWM逆变器输出误差分析及其补偿[J] .电工技术学报,2001,1(62):51-55.
[15] JONG-LICK LIN.A new Approach of Dead-time Compensation for PWM Voltage Inverters[J] .Circuit and system I:Fundamemtal Theory and Applications,IEEE Transactions on,2002,49(4):476-483
