干涉法检测钢化玻璃的研究

刘旭东，陈景玉，史颜波，刘会龙，董 渊

(1.长春市产品质量监督检验院，长春 130012;2.长春理工大学 理学院，长春 130022)

0 引言

随着玻璃工业技术的不断进步，建筑玻璃与汽车玻璃的制造工艺越来越复杂，对技术的要求也越来越高，钢化玻璃是将优质的浮法玻璃加热接近软化点时，在玻璃表面急速冷却，使压缩应力分布在玻璃表面，而张引应力则在中心层，因为有强大相等的压缩应力，使外压所产生的张引应力被玻璃强大的压缩应力所抵消，从而增加玻璃的安全度。因此辨别钢化玻璃的优劣，需要对其应力进行检测。

目前，变形测量主要应用数字全息法，运用反射式数字全息法测量不透明物体形变［1-2］，但是对于透明物体的变形测量，多集中在透明物体的定性检测，对于透明物体变形量的定量测量还未见报道，为此，本文提出了一种激光干涉法定量测量钢化玻璃的变形，激光干涉技术所具有的全场、灵敏、非接触、非破坏、精度高等一系列优点［3］，在干涉检测领域有着较广的发展前景。

1 干涉理论:

对于任意一列平面单色波［4］可以表示为:

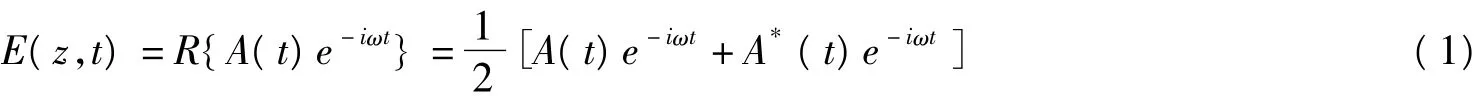
其中A是复矢量，分量为:Ax=a1(r)，Ay=a2(r)，Az=a3(r)。

式中aj和mj其中(j=1，2，3)是实函数，单色平面波中，振幅aj是常数，相函数mj可以表示为mj(r)=K·R-δj，其中K是光波传播矢量，δj是决定偏正态的相常数。由(1)式可以得到

现在假定，两个单色波E1和E2在空间P点叠加在一起。则P点的总电场为

可以得到

因此，P点的场强为:

式中:

J是这两列波的干涉项。

设A和B是这两列波的复振幅，其中Ax=，Bx=…，一般情况下这两列波是由不同空间传播到P点，所以这两个实位相mj和nj是不相同的。我们假定各个分量的位相差都一样，且都等于δ，则

式中，ΔS是这两个波从它们的共同光源P点的光程差，λ0是真空中的波长。用A和B表示，

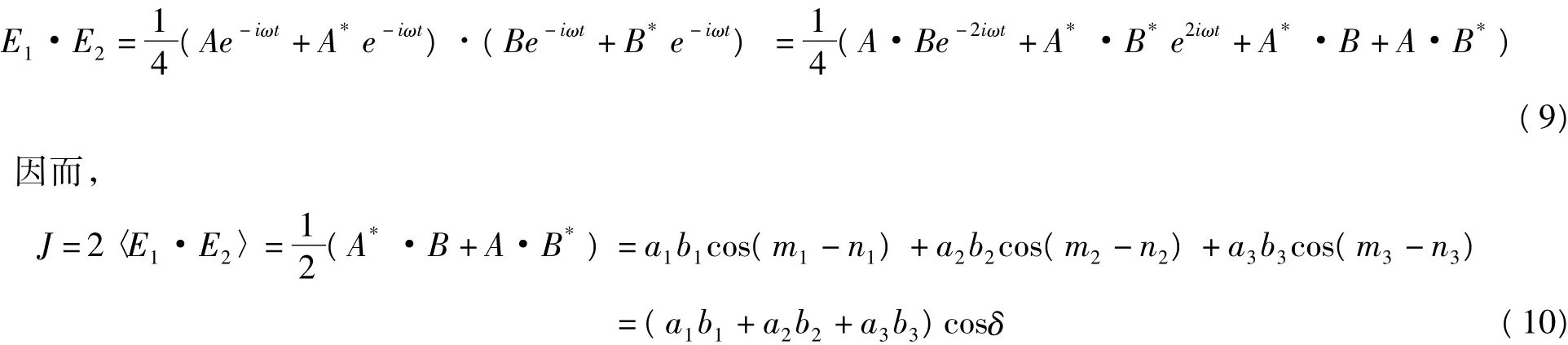
由(10)可以看出，干涉项决定于两列波的振幅分量和位相差。

现在我们讨论两线偏振光沿z方向传播，E的方向沿x轴，这时，a2=b2=a3=b3=0，由(6)和(10)可以得到

由(5)式可得到总的光场强度，

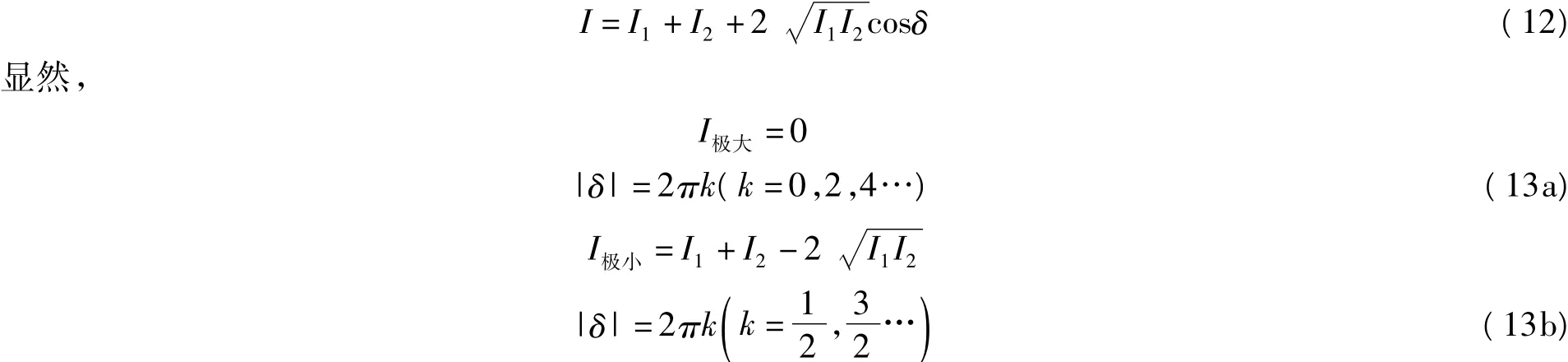
取一个特殊情况，当I1=I2时，(12)式可简化为

由此可知强度在极大值I极大=4I1和极小值I极小=0之间变化。

由MATLAB仿真的干涉场强度变化［5-6］，如图1所示。

图1 干涉场光强的分布

2 实验原理

图2是激光干涉检测钢化玻璃光路原理图，照明光束为准直激光束，该光束经分束镜S1分为沿水平方向照明的物光波和垂直向下的参考光波。水平方向光波透过待测的钢化玻璃，形成携带有需求信息的物光波，经M1反射至S2，通过半反半透镜S2反射到达CCD。参考光波经反射镜M2反射，透过半反半透镜S2到达CCD。钢化玻璃在外力F作用下，物光波和参考光波在空间叠加位置CCD处将形成干涉条纹。计算机对CCD上的干涉条纹进行连续采集并定位和跟踪，根据对应条纹位移量可以定量计算出钢化玻璃的量。

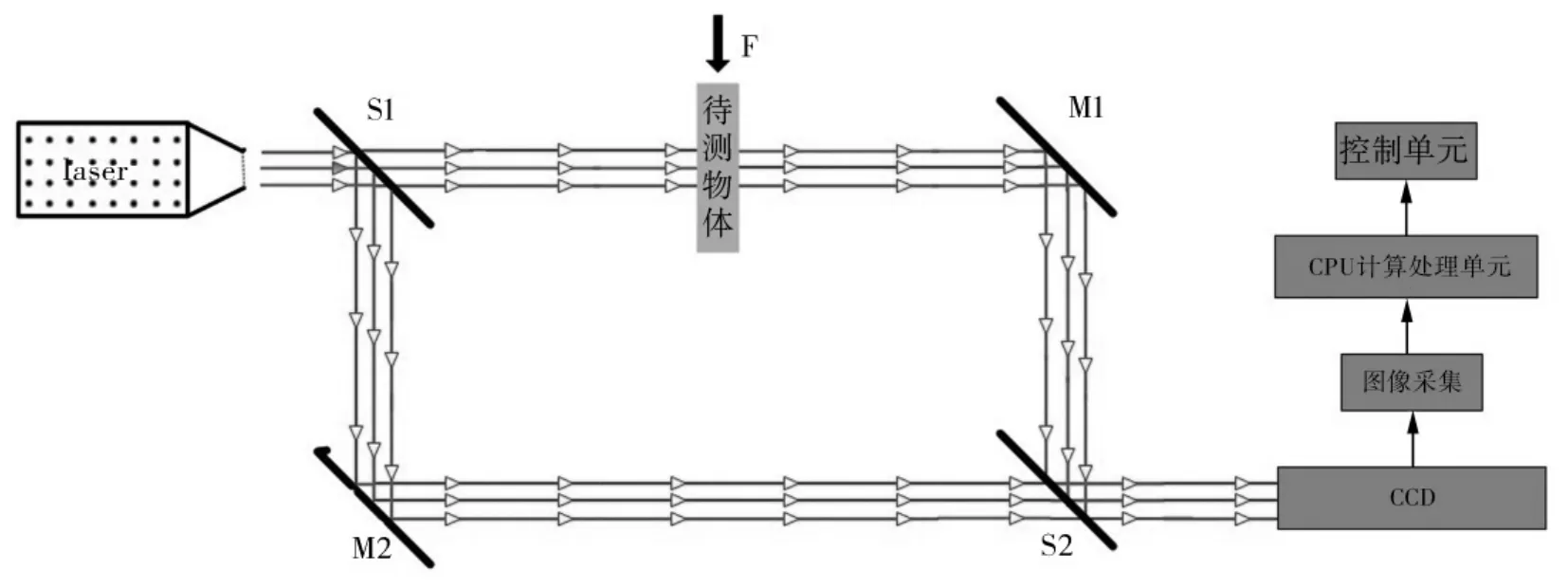
图2 激光干涉系统光路图

图3是实验所采集到的干涉条纹，并对干涉条纹进行标记，通过条纹的移动数目可以计算出玻璃的形变量［7-9］。

图3 实验采集的干涉条纹

如图4所示，钢化玻璃与光线传播的z轴垂直，光线通过钢化玻璃只有相位变化，传播方向不会发生改变。假设钢化玻璃在力F(方向沿y负向)作用下发生微小变形，现分析钢化玻璃内任意点受力F(x，y)与条纹移动量Δm(x，y)之间的关系，设钢化玻璃折射率为n，空气折射率n0，光波波长为λ，钢化玻璃的初始厚度为t(x0，y0)=d。

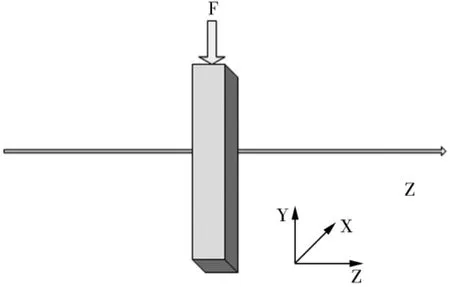
图4 钢化玻璃变形对光波相位的影响

则变形后的光波相位差δ(x，y)可以表示为:

其中 Δt(x，y)为钢化玻璃的变形量，由(13a)可得 δ(x，y)=2πΔm(x，y)，带入上式得:

Δt(x，y)是由于钢化玻璃受力引起的，Δt(x，y)与 Δm(x，y)之间的关系［10］

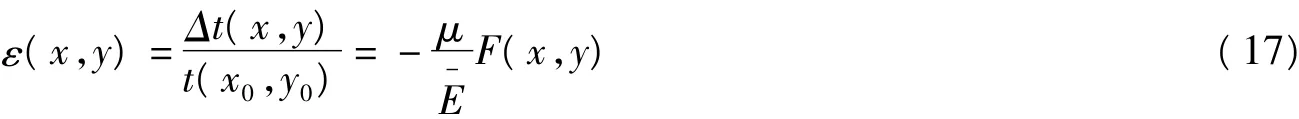
其中μ为泊松比， 为弹性模量，从而可得到F(x，y)大小为:

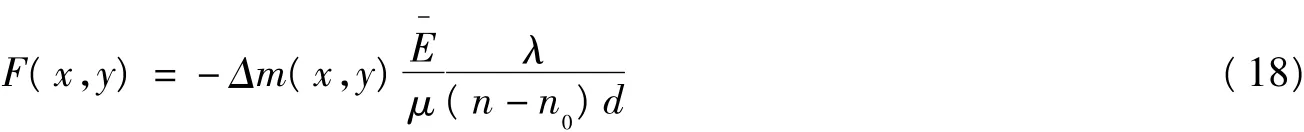
由(18)式我们可以看出，钢化玻璃受力F(x，y)和Δm(x，y)之间成线性关系，只要通过实验测量出Δm(x，y)，相应的力F(x，y)大小就可以知道。

3 结语

本文提出了干涉法检测钢化玻璃形变量的方法，通过理论推导，建立了钢化玻璃受力F(x，y)大小和条纹变化量Δm(x，y)之间的关系，该方法有检测精度高，检测速度快等优点。但是随着钢化玻璃的应用越来越广泛，如何更近一步提高测量精度，使得系统能完成高度线性和可重复性的测量，还有在保证测量精度的同时，进一步提高检测速度，降低仪器的成本等都是需要值得考虑的问题。干涉检测有全场、灵敏、非接触、非破坏、精度高等一系列优点，在无损检测方面有非常广的应用前景。

［1］周灿林，亢一澜.数字全息全息干涉法用于变形测量［J］.光子学报，2004，33(2):171-173.

［2］夏海廷，郭荣鑫，樊则宾.数字全息法测量透明物体变形的研究［J］.光电子激光，2011，22(7):1046-1050.

［3］赵锋，何卫平，魏从刚，吉锋.干涉检测算法的检测速度与精度的系统分析［J］.计算机工程与应用，2006，19(3):213-214.

［4］Max Born，Emil Wolf.Principles of optics［M］.Cambridge:Cambridge University Press，1999.

［5］徐代升，陶家友，吴健辉，陈松.单色光杨氏干涉图样计算机写真［J］.湖南理工大学学报，2009，22(3):28-31

［6］李直，赵洋，李达成.双激光束干涉条纹处理方法的研究［J］.光学技术，2001，27(4):310-312.

［7］李东光，张国雄.高速精密激光干涉测量的研究现状及其关键技术［J］.航空精密制造技术，1998，34(6):29-34.

［8］李竸白.小角度干涉条纹移动测量法［J］.福州大学学报，1987(2):46-54.

［9］王成龙，乔彦峰，任德新.干涉条纹检测微动位移的图像处理方法［J］.能计算机与应用，2011，1(4):11-13.

［10］徐芝纶.弹性力学［M］.北京:高等教育出版社，2006.