EPCBC密码旁路立方体攻击

赵新杰, 郭世泽, 王 韬, 张 帆

（1.军械工程学院计算机工程系,河北石家庄 050003;2.北方电子设备研究所,北京 100083;3.康涅狄格大学计算机科学与工程系,斯托斯康涅狄格州 06269）

0 引言

早在2008年美密会的Rump Session讨论中[1],Dinur和Shamir在高阶差分分析[2]基础上,提出了一种新的密码分析方法——立方体攻击（Cube Attack）,并声称只要密码算法的一个密文比特能够用公开变量和密钥相关变量的低次多元多项式表示,立方体攻击就能够攻破此密码算法。此外,立方体攻击的一大亮点是可在黑盒攻击场景下成功实施,即适用于密码算法未知情况下。目前,立方体攻击在流密码分析中卓有成效,已经对低轮的Trivium[3]、MD6[4]密码,甚至全轮Hitag2[5]、Grain-128[6]密码进行了成功分析。在分组密码Cube分析中,分组密码的多项式次数和项数随着轮数的延伸呈指数级增长,多项式的存储和表示十分困难。因此在传统密码分析场景下,立方体攻击仅对约简轮的分组密码分析有效,攻击遇到了NP-完全问题的瓶颈。

随着电子信息技术和普适计算的发展,RFID标签和无线传感器网络深入到人们生活的方方面面,如何在此类资源受限的环境下提供信息安全保障成为尚待解决的问题。轻量级密码算法正是在这种趋势上发展起来的,这些算法都要求在2000个门电路内硬件实现,特别适用于RFID标签等轻量级密码设备的加密需要。由于轻量级密码算法结构设计相对比较简单紧凑,中间状态的多项式复杂度较低,且轻量级的实现防护措施较少,极易遭受旁路立方体攻击的威胁。密码学者在仿真环境下对大量的轻量级密码进行了旁路立方体分析,如PRESENT[8-11],NOEKEON[12]、KATAN[13]。EPCBC密码[14]是Yap等在CANS 2011国际会议提出的轻量级分组密码,算法采用类PRESENT密码设计思想,其96位的密钥长度设计特别适用于RFID标签上的密码算法实现,加密效率优于AES和PRESENT。此外,设计者声称EPCBC可有效防御积分攻击、线性攻击、高阶差分攻击、滑动攻击,特别是改进的密钥扩展设计使其可有效抵抗相关密钥攻击。目前,在EPCBC抗旁路攻击安全性分析方面,尤其是抗旁路立方体攻击方面尚未发现有公开发表结果。

文献[11]基于8比特汉明重泄露模型,对PRESENT密码抗旁路立方体攻击能力进行了评估,在PRESENT算法设计已知情况下,28.95个选择明文可恢复PRESENT-80的72比特密钥,29.78个选择明文可恢复PRESENT-128的121比特密钥,攻击最大立方体大小仅为5;并对8位微控制器ATMEGA324P上的PRESENT密码进行物理实验,验证了攻击实际可行性。由于EPCBC密码基于PRESENT密码思想设计,根据文献[11]中攻击结果,认为EPCBC密码可能易遭受旁路立方体攻击。特别是,如果在EPCBC密码旁路立方体攻击中,提取的立方体大小仍然很小的话,攻击在黑盒场景下实施的复杂度应该较低。为了验证上述推测,基于汉明重泄露模型,对EPCBC密码抗黑盒旁路立方体攻击能力进行分析。结果表明:EPCBC密码易遭受黑盒旁路立方体攻击,攻击提取的最大立方体大小仅为5372个选择明文可恢复EPCBC（48,96）的48比特密钥,将其主密钥搜索空间降低到248610个选择明文可恢复EPCBC（96,96）的全部96比特主密钥。

1 相关知识

1.1 EPCBC算法设计

EPC（Electronic Product Code）[15]是EPCglobal提出的一种工业标准,标准主要利用Class 1 Gen 2的RFID标签作为EPC的载体,其中规定了低成本应用的标识符长度为96位。但是目前现有的分组长度和密钥长度均为96位的密码算法很少。比如PRESENT-80的分组长度为64位,需要执行2次加密才能生成标识,而AES-128一次加密则会浪费掉32位标识符。EPCBC[14]分组密码正是为了解决该问题而设计的,通过在PRESENT算法设计基础上进行改造而成。EPCBC有EPCBC（48,96）和EPCBC（96,96）两个变种,分别对应48位和96位分组,密钥长度均为96位,加密均使用32轮。EPCBC密码加密结构同PRESENT类似,只是分组长度、查找表次数和置换函数有所变化。

（1）加密过程

轮函数由轮密钥加、S盒代换、线性置换3部分组成,并在32轮使用后期白化操作。

轮密钥加 AK:48（96）位轮输入同48（96）位轮密钥进行异或。

赵天亮瞪着齐勇的背影说道:“这件事,不能就这么算完了!这可是我们新知青来到连队的第一天,我一定要代表新知青向连里抗议这件事!”

S盒代换层SL:将轮密钥加48（96）位输出查找12（24）个4进4出S盒,S盒沿用PRESENT密码设计。

线性置换层DL:输入的第i位被置换到输出的第P[i]位,P[i]计算方法为:

其中对于EPCBC（48,96）,n=12;对于EPCBC（96,96）,n=24。

（2）密钥扩展

为更好抵抗相关密钥攻击威胁,EPCBC设计了专门的密钥扩展算法,将加密轮函数引入到密钥扩展中,设计比PRESENT复杂,具体密钥扩展设计细节可参考文献[14]。

1.2 立方体攻击

立方体攻击将黑盒密码算法的输出比特看成有限域GF（2）上的包含公开变量（对于分组密码即明文变量）和密钥变量的未知多项式p。攻击分为两个阶段:预处理阶段,攻击者控制所有公开和密钥变量向密码算法询问p输出,等价于攻击者在密码分析中使用不同明文和密钥运行算法,分析得到选择明文、p输出和部分密钥比特相关多项式关系;在线阶段,攻击者生成选择明文,通过分析 p输出获取密钥比特相关多项式值,然后通过方程组求解方法获取密钥。

假定密码由 m个公共变量V={v1,…,vm}和 n个密钥变量K={k1,…,kn}组成。令X=V∪K,则密码任意输出比特可用关于X的一个多变量多项式f（X）表示,令多项式次数表示为Deg（f）。下面详细阐述攻击的两个阶段:

（1）预处理阶段

攻击者随机从 V中选取部分公开变量,令I表示所选取公开变量下标索引集合,I⊂{1,…,m},I即为一个立方体,大小为 λ,I中索引称为为立方体索引。tI表示所选取公开变量的乘积,又称极大项。f（X）可表示为

pS（I）是关于密钥变量的一个多项式,又称I相关的一个超多项式。qI中包括了所有不能被tI整除的子多项式。为更好的解释定义,这里给出一个简单例子

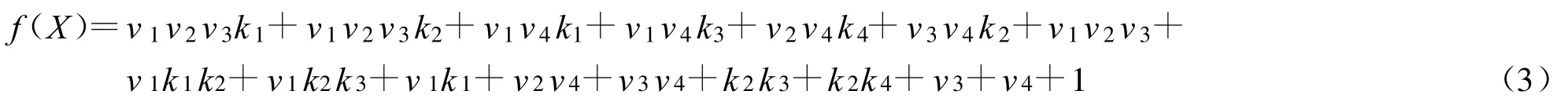
式（3）最高次数为4,包含8个变量、17个子多项式。将公开变量相同的子多项式合并后,f（X）可表示为

根据式（4）,以大小为3的立方体I={1,2,3}为例,1,2,3为立方体索引值。显然,tI=v1v2v3,pS（I）=k1+k2+1,qI=v1v4（k1+k3）+…+1。如果将 tI中的所有变量取遍0/1值,V中其他变量取0,则所得到的8个f（X）累积高阶差分即为pS（I）。应用类似方法,可得到4个线性立方体:

（2）在线阶段

在线阶段中,攻击者根据预处理阶段得到的立方体 I生成2λ个选择公开变量,通过问询密码算法得到p的输出,并计算高阶差分得到对应的超多项式pS（I）的值,然后利用代数方程求解方法恢复相关密钥变量K。

需要说明的是,在线阶段主要是通过问询密码得到 f（X）输出,验证预处理阶段得到的立方体 I和超多项式pS（I）之间关系是否存在。在已知密码设计时,可将 f（X）精确的表示出来,通过合并极大项的方式得到 I和pS（I）;在未知密码设计时,攻击者可以穷举或者随机选取 I和pS（I）,通过在线阶段验证二者关系,并求解出密钥。

1.3 旁路立方体攻击

在分组密码立方体攻击中,多项式 f（X）的次数和项数随着轮数延伸呈指数级增长,在有限复杂度内将其存储和表示是一个NP-完全问题,攻击仅对约简轮分组密码有效。而当考虑到密码实现物理泄露时,通过各种旁路泄露分析得到的中间状态可作为天然的多项式f（X）输出,等效于约简轮立方体攻击的场景。更重要的是,旁路信息的引入使得立方体攻击对分组密码安全性可构成现实威胁,二者的结合即称为旁路立方体攻击。

2 EPCBC旁路立方体攻击

2.1 汉明重泄露模型

旁路立方体攻击中,泄露模型的选择取决于攻击者的能力,泄露模型不同时目标比特的多项式 f（X）表示方法不同。对于汉明重泄露模型,由于泄露汉明重的一个比特和对应的中间状态还存在关系,因此还需要进行一定的转换。以一个字节 X=（x7,x6,x5,x4,x3,x2,x1,x0）的汉明重泄露为例,假如其汉明重Y=H（X）=（y3,y2,y1,y0）,x0和y0分别表示X和Y最低位。Y可用X表示如下

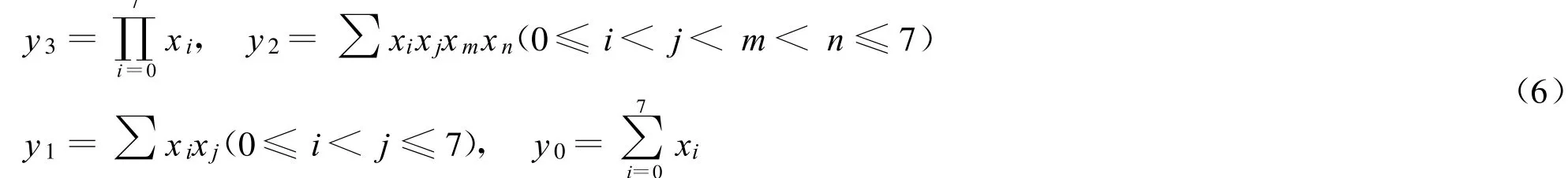
根据式（6）可知,Y的每一个比特值都可以作为旁路立方体攻击中利用的泄露比特。其中y0的次数是最低的,意味着其对应f（X）的复杂度是最低的,可以作为汉明重泄露的最佳泄露利用比特。另外,y3,y2,y1也可以在攻击中使用,但是对应 f（X）复杂度可能较高,需要一些特殊的算法去提取超多项式。

2.2 黑盒旁路立方体攻击

旁路立方体攻击继承了立方体攻击的优点,可在未知算法设计下实施。下面给出黑盒旁路立方体分析的算法。

步骤1:攻击者设定立方体中明文变量的数量和超多项式中密钥变量的数量,并根据前面设定穷举生成立方体I和超多项式 pS（I）;

步骤2:利用I生成选择明文和随机密钥,采集加密实现物理泄露并分析推断出泄露比特位;

步骤3:测试pS（I）的值是否等于这些选择明文对应泄露比特的高阶差分;

步骤4:如果步骤3成立,则重复步骤2～3共N次。如果 N次步骤3结果都成立,则步骤1中的立方体 I和超多项式pS（I）是有效的;否则无效,攻击者重新返回步骤1。

根据上面算法,黑盒旁路立方体攻击复杂度取决于选择明文变量和超多项式中密文变量数量,并随着二者的增加呈指数级增长。选择明文变量数量受密码分组长度限制,超多项式的数量受密码支持密钥长度和攻击者选择超多项式的阶数限制。在实际攻击中,为降低攻击数据复杂度,一个好的黑盒立方体攻击应该具有选择明文变量（立方体大小）和超多项式中密钥变量数量较小的特点。

应用2.2节方法,基于汉明重泄露模型,对EPCBC（48,96）和EPCBC（96,96）分别进行了黑盒攻击。攻击中,设定最大立方体大小仅为5,超多项式中密钥变量数量最大为3,N=100。参考文献[11]中泄露比特位置,选取EPCBC加密第三轮轮密钥加字节汉明重量的最低泄露比特进行密钥分析。

2.3 EPCBC（48,96）攻击

EPCBC（48,96）攻击中,利用加密第三轮轮密钥加前两个字节的最低位分别作为泄露比特,成功提取出48个超多项式,使用372个选择明文恢复第一轮48比特密钥,将其主密钥搜索空间降低到248。攻击结果如表1所示。

表1 EPCBC（48,96）黑盒旁路立方体攻击结果

2.4 EPCBC（96,96）攻击

EPCBC（96,96）攻击中,利用加密第三轮轮密钥加的前两个字节的最低位分别作为泄露比特,成功提取出96个超多项式,使用610个选择明文直接恢复96比特密钥。攻击结果如表2所示。

表2 EPCBC（96,96）黑盒旁路立方体攻击结果

3 结束语

基于8位汉明重泄露模型,对EPCBC密码抗黑盒旁路立方体攻击能力进行评估。结果表明:EPCBC密码易遭受黑盒旁路立方体攻击,如果攻击者能够精确获取加密过程汉明重信息泄露,提取出的立方体大小最大仅为5;372和610个选择明文可分别恢复EPCBC（48,96）的48比特密钥和EPCBC（96,96）的全部96比特主密钥;EPCBC密码实现应增加旁路立方体攻击的防护措施以提高其安全性。

[1] I Dinur,A Shamir.Cube Attacks on Tweakable Black-box Polynomials[EB/OL].http://eprint.iacr.org/2008/385.pdf.

[2] X Lai.Higher Order Derivatives and Differential Cryptanalysis[J].Communications and Cryptography,227-233.

[3] I Dinur,A Shamir.Cube Attacks on Tweakable Black-box Polynomials[A].EUROCRYPT 2009[C].LNCS,2009,5479:278-299.

[4] J P Aumasson,I Dinur,W Meier,et al.Cube Testers and Key Recovery attacks on Reduced-Round MD6 and Trivium[A].In FSE 2009[C].LNCS,2009,5665:1-22.

[5] S Sun,L Hu,Y Xie,et al.Cube Cryptanalysis of Hitag2 Stream Cipher[A].In CANS 2011[C].LNCS,2011,7092:15-25.

[6] I Dinur,A Shamir.Breaking Grain-128 with Dynamic Cube Attacks[A].In FSE 2011[C].LNCS,2011,6733:167-187.

[7] I Dinur,A Shamir.Side Channel Cube Attacks on Block Ciphers[EB/OL].http://eprint.iacr.org/2009/127.pdf.

[8] L Yang,M Wang,S Qiao.Side Channel Cube Attack on PRESENT[A].CANS 2009[C].LNCS,2009,5888:379-391.

[9] S F Abdul-Latip,M R Reyhanitabar,W Susilo,et al.Extended Cubes:Enhancing the cube attack by Extracting Low-Degree Non-linear Equations[A].ASIACCS 2011[C].2011:296-305.

[10] X Zhao,S Guo,F Zhang,T Wang,et al.Enhanced Side-Channel Cube Attacks on PRESENT[J].IEICE T RANS.FUNDAMENTALS,2003,E96-A（1）.

[11] X Zhao,S Guo,F Zhang,et al.Efficient Hamming Weight-based Side-Channel Cube Attacks on PRESENT[J].The Journal of Systems&Software（2010）,doi:10.1016/j.jss.2012.11.007.

[12] S F Abdul-Latip,M R Reyhanitabar,W Susilo,et al.On the Security of NOEKEON against Side Channel Cube Attacks[A].ISPEC 2010[C].LNCS,2010,6047:45-55.

[13] G V Bard,N T Courtois,J Nakahara,et al.Algebraic,AIDA/Cube and Side Channel Analysis of KATAN Family of Block Ciphers[A].INDOCRYPT 2010[C],LNCS,2010,6498:176-196.

[14] H Yap,K Khoo,A Poschmann,et al.EPCBC-A Block Cipher Suitable for Electronic Product Code Encryption[A].In CANS 2011[C].LNCS,2011,6715:34-45.

[15] EPC global.EPC Tag Data Standard Version 1.5.EPC global Specification[S].August 2010,available at www.gs1.org/gsmp/kc/epcglobal/tds/