基于BP神经网络的无刷直流电机控制器优化设计
2012-09-21程耕国赵玉寿
王 玲,程耕国,赵玉寿
(武汉科技大学 信息科学与工程学院,武汉 430081)
基于BP神经网络的无刷直流电机控制器优化设计
王 玲,程耕国,赵玉寿
(武汉科技大学 信息科学与工程学院,武汉 430081)
无刷直流电机是一个多变量、强耦合的非线性系统,用常规的线性控制方法很难达到理想的控制效果。为了克服常规PID控制方法的不足,应用了BP神经网络对速度控制器的PID参数进行了优化设计。使用MATLAB仿真结果表明,采用BP神经网络这种控制方式的无刷直流电机调速系统具有良好的动态性能和稳态精度,能达到进一步优化控制系统性能的目的。
无刷直流电动机;BP神经网络;速度控制系统
引言
无刷直流电机由于采用永磁转子,其能量密度也比交流电机大,结构简单和具有良好的调速性能,在工业中得到了广泛的应用。但由于该电机是一个多变量、强耦合的非线性系统,如电枢反应的非线性、负载扰动、电阻变化等,使得难以用一个精确的数学表达式来描述永磁无刷直流电机的电磁关系,所以使用常规的 PID控制方法很难达到理想的控制效果。
人工神经网络是由大量神经元处理单元广泛互联形成的网络,是一个高度复杂的非线性动力学系统,特别适合处理需要同时考虑许多因素和条件的、不确定和模糊的信息处理问题。反向误差传播算法(back propagation以下简称BP网络)是对非线性可微分函数进行权值训练的多层前向神经网络,是目前人工神经网络实际应用中应用最广,效果最好的一种模型方法,它有较好的持久性和适时预报性。本文用BP神经网络来优化控制器的比例、积分、微分参数,仿真表明,该方法可以获得较好的控制效果。
1 PID控制基本原理
常规PID控制系统的原理图,如图1所示。
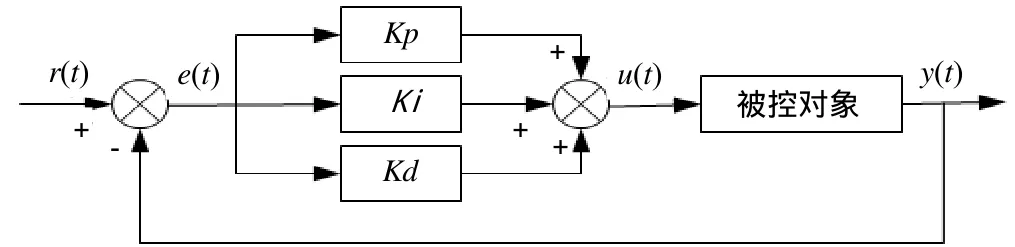
图1 常规PID控制器的原理图
常规PID的控制规律为:
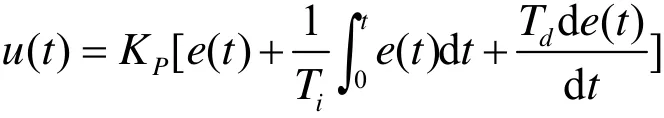
式中:KP——比例系数;Ti——积分时间常数;Td——微分时间常数; e( t)——设定值 r( t)与实际输出值 y ( t)之差。写成增量式PID控制方式为:

式中:Kp,Ki,Kd即要优化的参数。
2 BP神经网络PID控制器设计
2.1 BP神经网络PID控制器基本结构
BP神经网络无刷直流电机调速系统基本结构如图2所示。
由图2可知,常规PID控制器对无刷直流电机的转速加以闭环控制,控制器参数Kp,Ki,Kd通过神经网络在线整定。神经网络的主要作用是根据系统的运行状态,对PID控制器参数加以调节,以达到期望最优的性能指标。即神经网络的输出作为传统PID控制器的可调参数Kp,Ki,Kd,通过神经网络自身的不断学习,加权系数的调整,来达到对转速性能指标的最优化,以充分发挥神经网络的优点所在。在神经网络自学习控制器中,采用BP神经网络构建自学习控制器,并由其实现数字增量式PID控制器的输入输出对应关系。
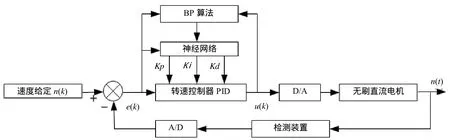
图2 BP神经网络无刷直流电机调速系统框图
2.2 BP神经网络PID控制算法
BP神经网络具有逼近任意非线性函数的能力,而且结构和学习算法简单明确,通过网络的自身学习,可以找到某一最优控制规律下的PID参数。三层BP神经网络结构如图3所示。

图3 三层BP神经网络结构图
网络输入层的输入为:
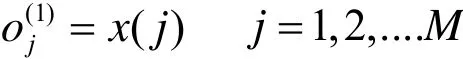
式中:M代表输入变量的个数,其大小取决于被控系统的复杂程度。
网络隐含层的输入、输出为:

式中: wi(j2)代表隐含层的加权系数;上角标(1)、(2)、(3)分别代表输入层、隐含层和输出层。隐含层神经元活化函数取正负对称的Sigmoid函数:
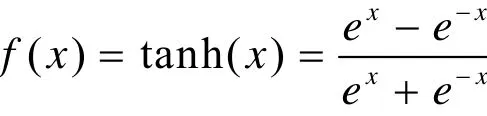
网络输出层的输入输出为:

输出层输出节点分别对应三个可调参数Kp、 Ki、Kd。由于 Kp、 Ki、 Kd负值,所以输出层神经元的活化函数取非负的Sigmoid函数,即:

取性能指标函数为:
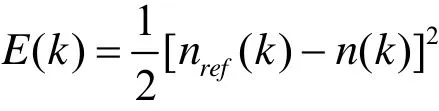
按照梯度下降法修正网络的权系数,即按 ()E k对加权系数的负梯度方向搜索调整,并附加一个使搜索快速收敛于全局极小点的惯性项:

式中:η为学习速率;α为惯性系数。
按照梯度下降法修正网络权系数的公式为:
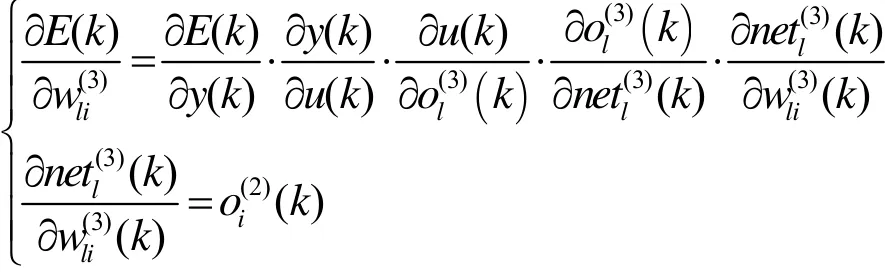
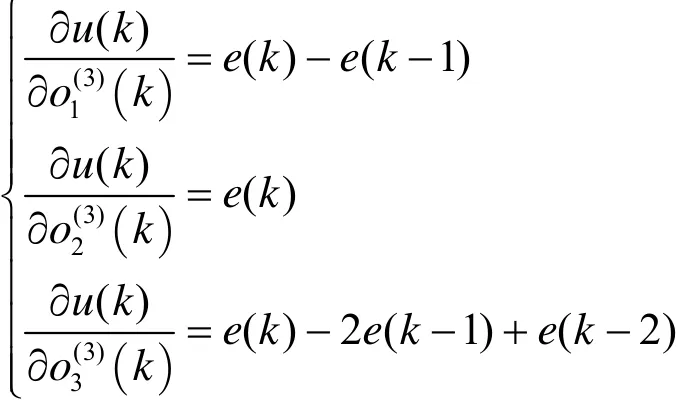
输出层权系数的学习算法为:
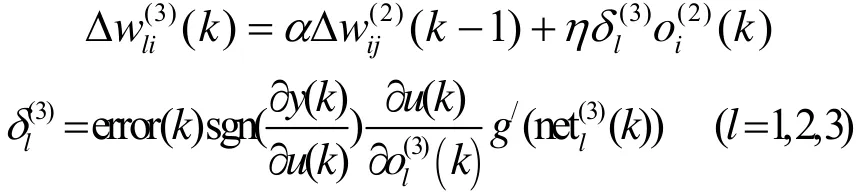
隐含层权系数的学习算法为:
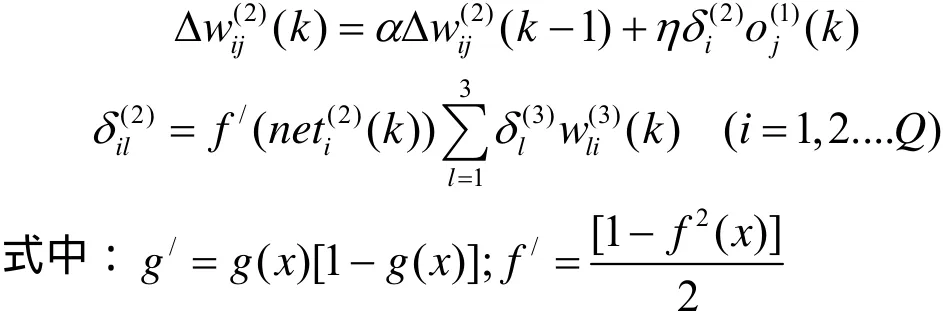
2.3 BP神经网络PID的运算步骤
BP神经网络电机转速PID控制器的运算步骤如下:
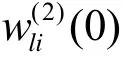
(2)采样得到t = KT时刻的 nref(k)和 n( k)值,并计算出该时刻的误差数值为: e( k ) = nref(k ) - n ( k );
(3)计算神经网络各层神经元的输入、输出,其输出即为PID转速控制器的三个可调参数 Kp、Ki、Kd;
(4)计算出数字PID转速控制器的输出量 ()u k;

(6)k值自增1,返回步骤(2),直到误差满足要求为止。
3 仿真分析
为了验证控制方案的有效性,利用 Matlab对 BP神经网络PID控制器进行仿真分析,并与常规PID控制器进行对比分析。其中,学习速率η=0.34和惯性系数α=0.05;无刷直流电机参数为:额定电压400V,额定转速为800r/min,电枢绕组相电阻3.4Ω,转动惯量0.00162kg m·;反电动势系数为0.5188V/rad。仿真比较曲线如图4所示。仿真时,设置在t=2.5s时突然增加负载,结果如图5所示。
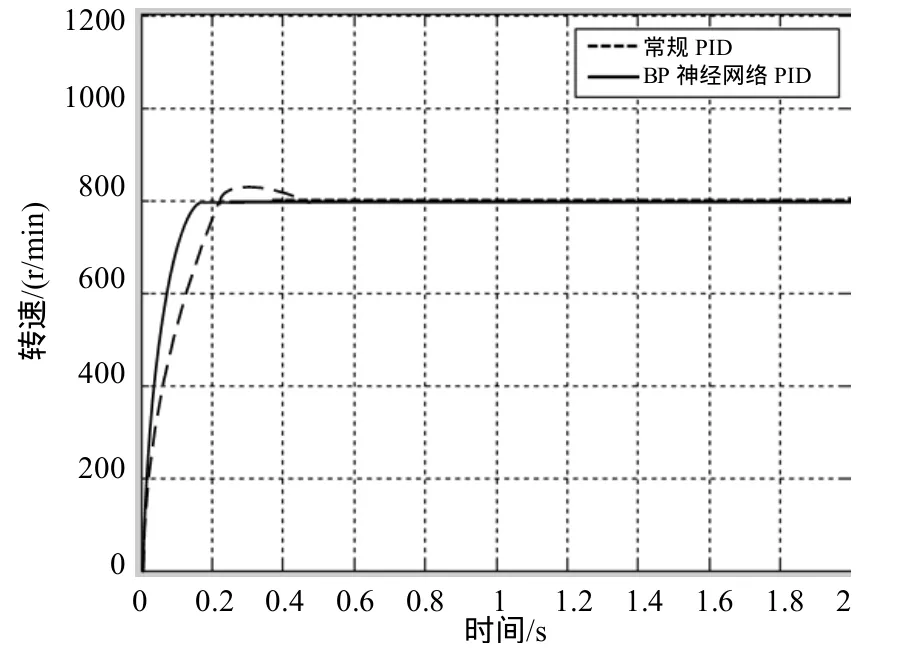
图4 电机空载时的运行情况

图5 2.5s突加负载的运行情况
从上图可以看出:利用BP神经网络PID控制的电机转速比常规PID响应快、调节时间短,具有更加优良的静态和动态性能。在负载突变的情况下,神经网络PID控制系统具有较小的扰动。
4 结束语
从仿真结果可以看出,和传统的PID控制相比,神经网络 PID控制可以实现实时自校正,具有调节时间短、鲁棒性强等优点,有比较好的控制效果,证明了神经网络PID控制器具有良好的参数整定性能,能有效的优化参数,从而进一步提高了控制器的性能。为非线性调速系统的控制、建模、辨识提供了有效的方法与工具。
[1] 董正良. 无刷直流电机 BP神经网络控制的研究[D]. 西安: 西安电子科技大学, 2010.
[2] 姜忠山, 宋超, 朱飞翔. 遗传算法优化BP神经网络在转速 PID控制中的应用[J]. 兵工自动化,2009, 28(3): 52-55.
[3] 龙驹. 永磁无刷直流电动机转速控制系统的优化设计[M]. 成都: 西南交通大学出版社, 2006.
[4] 刘金锟. 先进PID控制MATLAB仿真(2版) [M].北京: 电子工业出版社, 2004.
[5] 戴莹. 基于 BP神经网络的无刷直流电机[D]. 合肥: 合肥工业大学, 2007.
[6] 焦竹青, 屈百达, 徐保国. 基于BP神经网络PID控制的 BLDCM 调速系统[J]. 微计算机信息,2007, 23(4): 112-113.
[7] 付丽辉. 基于改进型 BP神经网络的无刷直流电机调速系统的应用研究[J]. 大庆师范学院学报,2010, 30(6):29-32.
审稿人:许善春
The Improved Design of Brushless DC Motors Controller Based on BP Neural Network
WANG Ling, CHENG Gengguo, ZHAO Yushou
(School of Information Engineering, Wuhan University of Science and Technology, Wuhan 430081, China)
s: The brushless DC motor is a multi-variable, strong coupling and non-linear system. With conventional linear control methods are difficult to achieve the desired results. To overcome the shortage of conventional PID control method, use BP neural network improved the PID parameters of speed controller. MATLAB simulation results show that the BP neural networks using in the brushless DC motor speed control system has good dynamic performance and steady precision, and achieve the purpose of optimizing the control system performance.
brushless DC motor; back propagation neural networks; Speed control system
TM33
B
1000-3983(2012)01-0019-03
国家自然科学基金项目(60074032)
2011-04-17

王 玲(1987-),硕士研究生,测技术与自动化装置专业,主要研究方向为智能控制。
