复杂曲面五轴加工局部干涉处理技术研究
2012-09-21闫献国田锡天
杜 娟, 闫献国, 田锡天
(1. 太原科技大学机电工程学院,山西 太原 030024;2. 西北工业大学机电工程学院,陕西 西安 710072)
局部干涉处理作为复杂曲面三轴和五轴数控加工中的关键问题之一,长期以来,得到了广泛深入的研究。目前,已经提出了很多有关的局部干涉判断和处理方法。其中最常见的方法之一是距离法,即通过计算加工表面与刀具表面的距离,来判断是否有干涉发生[1-5],在计算两者之间距离时,提出了通过计算三角片面与刀具表面的距离来代替工件表面与刀具表面之间距离的方法,这种方法需要事先将加工表面离散成三角片面。该方法不但处理和计算较复杂,而且在这些文献中,大都主要侧重于干涉检测和处理技术的研究,而对三角片面的离散,尤其是检测区域和检测点的自动生成却没有进行深入研究,仅仅给出了检测区域和检测点的一个定性描述。Ahmet[5]提出了基于参数区域的检测区域和检测点的确定方法,并通过计算切触点与检测点连线的最大倾角来判断是否有干涉发生,这种方法虽然技术上可行,但计算量过大。Jensen and Anderson[6]提出了通过多项式来判断刀具表面与加工表面的下偏差等距面之间是否相交,假如相交,则说明有干涉产生。局部干涉处理的另一类主要方法是微分几何法,即通过刀具和被加工零件切触点处的曲率分析来对刀具的局部干涉进行检查和修正。Stanislav S[7]、Cha-Soo[8]和 Rao A[9]等人研究了垂直于刀具进给方向的法截面内刀具同加工曲面的几何啮合状态,通过检测刀具和切触点处的曲面曲率是否匹配来进行局部干涉的判断,并通过调整刀具尺寸或刀具姿态来消除干涉现象;文献[10][11]提出了密切曲率法,即根据在密切面内刀具与曲面曲率的吻合状态来进行局部干涉的检测和处理;Lee[12]和Than Lin[13]等人则在切触点处平行于刀具进给方向和垂直于进给方向的两个法截面内,分别将刀具的有效切削曲率和曲面的有效曲率半径进行比较,从而进行局部干涉的判断和处理。由于目前基于微分几何法的局部干涉判断和处理方法大都只限于在进给方向和垂直于进给方向的法截面内进行曲率比较,而没有考虑到刀具和曲面在各个方向上的曲率变化,同时也没有考虑到切触点处邻近区域的干涉问题。因此,基于法截面的二维分析方法实际上无法真实描述刀具与被加工曲面之间的相对运动[14]。
环形刀由于其具有良好的切削性能,且不易磨损等优点,因此被广泛应用在复杂曲面的五轴数控加工中。与平底刀不同,环形刀的切削部位是圆环面,因此,在切触点处的切平面上,沿着各个切线方向刀具都有可能和被加工曲面发生过切。为此,本文提出了一种基于全曲率匹配的局部干涉检测方法,该方法将用于切触点处由于刀具曲率和被加工曲面曲率不匹配的而引起的局部干涉问题。此外除了考察切触点处的过切干涉外,还对切触点邻近区域的过切问题(通常也称为后跟过切)进行了研究,提出了一种基于方形点阵的检测区域及检测点的自动生成方法,详细内容见下文所述。
1 五轴数控加工模型及局部干涉
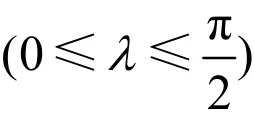

图1 曲面五轴加工模型及各坐标系
2 局部干涉的判断和处理
本文中,局部干涉的判断和处理主要分两步进行,首先对切触点处的局部干涉进行判断和处理,采用全曲率匹配原则确定该点处无干涉加工时的初始倾角λ1,然后再考察其邻近区域内的局部干涉问题,并由此确定最终的无局部干涉的刀具倾角λ2。
2.1 基于全曲率匹配的(切触点处)干涉判断和处理
为了实现在切触点处刀具曲面与被加工曲面在各个切向方向上的曲率匹配,首先需要确定其各自的主曲率,其计算方法如下所示。
2.1.1 加工曲面及刀具切削曲面的主曲率计算
根据微分几何知识,对于复杂曲面上非脐点的任意点P处其主曲率(最大法曲率及最小主曲率)可由下列方程得出[15]
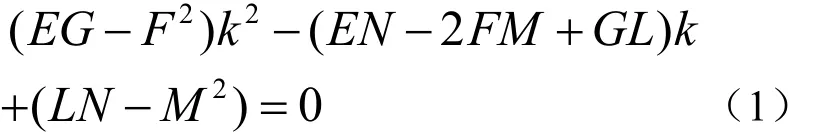
上式中,E、F、G分别为曲面的第1类基本量,L、M、N为曲面的第2类基本量,其计算公式如下

在公式(2)中,n为曲面的单位法矢量,下角标符号表示曲面r(u,v)对该符号的偏导数。当给定曲面上一个确定的点时,其对应的第1类基本量E、F、G和第2类基本量L、M、N便可由上式求出,将其带入方程(1)中,便可求得该方程两个不同的实根,其分别为该点处的最大法曲率Kmax和最小法曲率Kmin。
由于环形铣刀是一个典型的回转曲面,根据微分几何理论可知其最大主方向和最小主方向分别为刀具曲面经线(子午线)和纬线的切线方向[15],由 Meusnier定理及其主方向便可求出当刀具倾角为λ时环形铣刀圆环曲面的最大法曲率和最小法曲率为

2.1.2 刀具半径的选择
当在切触点CC处的任意方向上,刀具曲面的法曲率小于被加工曲面的法曲率时,就会产生局部干涉(过切)现象,因此,为了保证在切触点处沿任意方向上不发生过切现象,可以通过使刀具曲面的最小法曲率大于或等于切触点处被加工曲面的最大法曲率来避免干涉的产生。在每一个切触点处,被加工曲面的最大法曲率Kmax是确定值,而刀具曲面的最小法曲率kmin由公式(3)可知,其不但取决于刀具倾角λ,而且还与刀具半径R1和R2有关,因此在加工之前首先应选择合理的刀具半径。
在选择刀具半径之前,首先要对被加工曲面的形状进行判别,即判断是凸面还是凹面。曲面的凸凹可根据该点处的两个主曲率Kmax和Kmin符号来进行判断,这里规定曲面法矢向量n的正方向为Z轴的正方向,则当Kmax<0且Kmin<0时,说明是凸椭圆点,在本文中规定,当两个主曲率的符号都为负值时,认为曲面为凸面,其余都统称为凹面。当加工曲面为凸面时,不存在局部干涉问题,而当曲面为凹面时,则有可能发生局部干涉,因此,刀具半径的选择主要根据被加工曲面凹面最小法曲率半径来确定,即在被加工曲面凹面上对应最大法曲率的切触点处,使得刀具最小法曲率大于等于凹面的最大法曲率。由公式(3)可知,随着刀具倾角λ的增大,刀具最小法曲率也跟着增大,但在实际加工中,尽可能取较小的刀具倾角,因为其值越小,加工带越宽,加工效率越高[16]。但是,若倾角取得过小,由公式(3)可知刀具最小法曲率也变得很小,这样在切触点处很容易发生过切,因此,应当根据表面形状选择一个合适的倾角来选择刀具。假设选择倾角为λ0,则刀具的半径值R1和R2可由下列公式得出
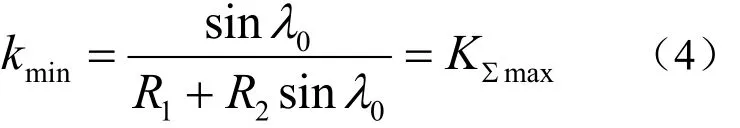
上式中KΣmax为加工曲面凹面上最大的法曲率。由于方程(4)中有两个未知数R1和R2,为了求解R1和R2的值,本文采用迭代的方法来寻求适合解,刀具半径的选择过程见图2所示。由于刀具半径是由被加工曲面凹面的最大法曲率决定的,因此在凹面上其它切触点处,如果该点处最大法曲率小于凹面的最大法曲率时,由公式(3)可知,其对应的倾角λ<0λ,即在这些切触点处,只需要较小的刀具倾角就可实现无局部干涉的加工。

图2 刀具半径的选择过程
2.1.3 切触点处干涉的判断与处理
倾角λ直接关系到零件的加工效率,而摆角ω主要是影响切削带宽的对称性,对加工效率影响较小,且当ω=0o,可得到最大的切削带宽,因此在实际加工中,一般取ω= 0o[7,13,17-19],本文中亦设ω= 0o。在加工之前首先设置初始倾角λ=5o,如果被加工曲面是凸面,则不存在干涉问题,可取λ=5o进行加工,以获得尽可能高的加工效率。当被加工曲面为凹面时,则需要对干涉进行判断和处理。在切触点处,首先根据给定的初始倾角计算刀具的最小法曲率,并判断其是否大于等于该点处曲面的最大法曲率,如果是,则以初始倾角进行加工,否则增大倾角,直到其等于或大于加工曲面最大法曲率为止。
当确定出满足切触点处不干涉的初始倾角λ1后,还需要对切触点邻近区域的局部干涉进行判断和处理。若该区域无干涉产生,则以初始倾角λ1进行加工,否则通过增大倾角λ值来消除邻近区域的局部干涉,如图3所示。

图3 切触点邻近区域局部干涉及处理
2.2 切触点邻近区域的局部干涉判断和处理
2.2.1 检测区域及初始检测点的确定
在对切触点邻近区域进行干涉检查之前,首先应建立检测区域及确定检测点。为了保证刀具底端在加工曲面上投影区域内的点都位于检测区域内,本文提出了一种基于正方形网格划分的方形点阵检测区域和检测点的确立方法。首先根据刀具半径R1和R2确定出正方形边长为2(R1+R2),然后在刀具切触点CC处,即图 4中P0,0点,从该点出发沿着刀具进给方向的反方向依次计算出点P0,j(j=1,2,…,m),即图4中带叉形符号的点。假设正方形划分间隔为Δl,则m=2(R1+R2)/Δl。当所有的P0,j点确定之后,再分别以P0,j点为基点,沿垂直于刀具进给方向,即图4中的列向方向,分别确定出P0,j点所在列上其它所有点Pi,j(i=±1, ±2, …, ±n)的坐标值,这里n=(R1+R2)/Δl。Δl取值越小,则检测精度越高。
假设切触点P0,0处对应的径矢为r(u0,v0),点P0,j(j=1,2,…,m)处的径矢为r0,j(u,v),则其可由下列式子得出

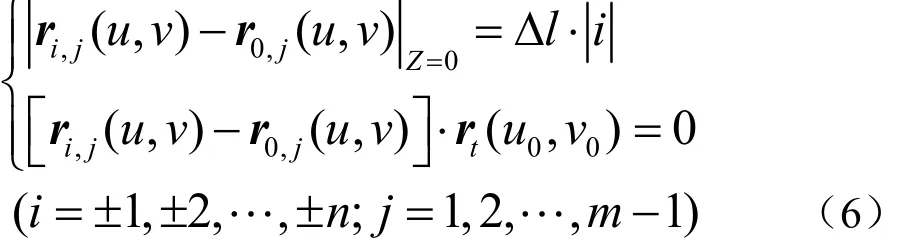
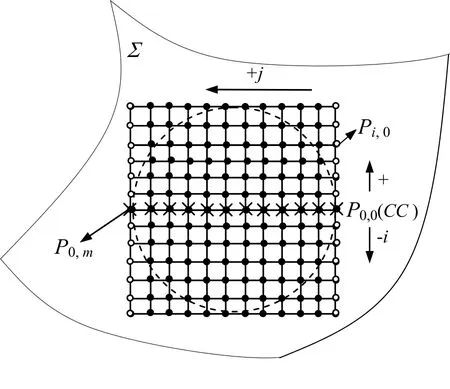
图4 检测区域及检测点
通过公式(5)和(6)计算出的点集即为图 4中方形网格中的实心黑点,在本文中,这些网格黑点即作为初始的候选检测点。刀具在有倾角的情况下实际投影为一个椭圆,椭圆的长径为刀具半径(R1+R2),而在本文中是以长径为半径确立了一个圆形投影区域,如图4种所示虚线圆,这样就能充分保证实际椭圆形投影区域内的点都落在了圆形投影区域内。从图4中可以看出,大部分网格黑点落在圆形区域内,少数落在圆形区域外,由于我们只对落于圆形区域内的点进行干涉检验,因此在进行干涉检查之前,还需要从初始检测点中选出有效检测点。
2.2.2 有效检测点的筛选
当确定出初始检测点之后,接着需要进行有效检测点的选择,即只对落于刀具投影区内的黑点进行干涉检查。为了判断初始检测点是否落于刀具投影区域内,首先将方形检测区域内的初始检测点转换为刀具坐标系中的点,然后再对其进行有效点的判断。由曲面坐标系向刀具坐标系转换的矩阵公式如下

上式中,TMM表示从工件坐标系到刀具坐标系的转换矩阵,TLM和LMM则分别表示从切触点处的局部坐标系到刀具坐标系以及工件坐标系到局部坐标系的转换矩阵。由图1所示的坐标系关系,可以得出其转换矩阵为


若在切触点CC处,其确定的初始倾角λ=λ1,摆角ω=0,将其代入式(9)可得
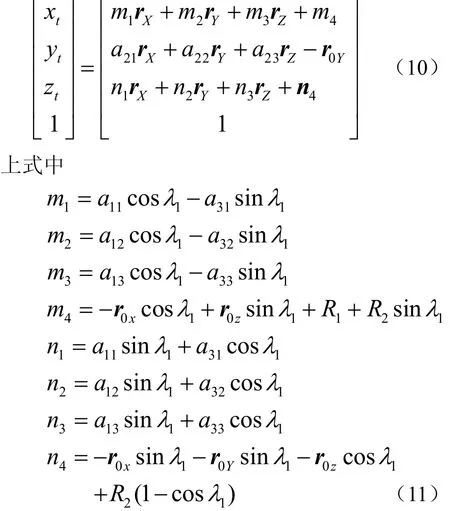
当将检测区域内的初始检测点转变为刀具坐标系中的点后,首先要判断该点是否落在刀具的投影区域内。假设刀具坐标系中点的坐标值为(xt,yt,zt),则当点的坐标值满足下列式子时,说明该点位于刀具投影区域内
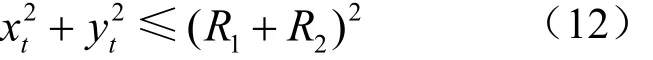
在本文中,主要对投影区域内除切触点外其邻近区域的点进行干涉判断,即有效干涉检测点既要满足式(12),还要满足下列式子

将式(10)中的坐标值分别代入上式(12)和(13)得

公式(14)即为判断初始检测点是否为有效检测点的检验公式。为了提高检测效率,本文只对满足式(14)的有效检测点进行干涉的判断和处理。
2.2.3 干涉的检查及处理
当有效检测点位于刀具底平面的下方时,则刀具与加工曲面不发生干涉,因此可以通过检测有效点是否位于刀具底平面下方来判断是否有干涉发生,其判断公式如式(15)所示。若zt>0,说明检测点位于刀具底平面上方,即刀具与被加工曲面之间有干涉产生。

局部区域的干涉判断和处理过程如下:
1) 首先依次对所有有效检测点的zt值进行判断,若都满足式(15),则说明没有局部干涉产生,这时就以切触点处产生的初始倾角λ1进行加工;
2) 若存在某些点,其zt>0,则找出这些点中最大的zt,其最对应的zt值为

3) 为了消除干涉,则应增大倾角λ,直到使得原先拥有最大zt值的点位于刀具底平面上。假设这时对应新的倾角为λ2,则其值可由下列方程组得出

由公式(11)和(12)可将上式方程组写为
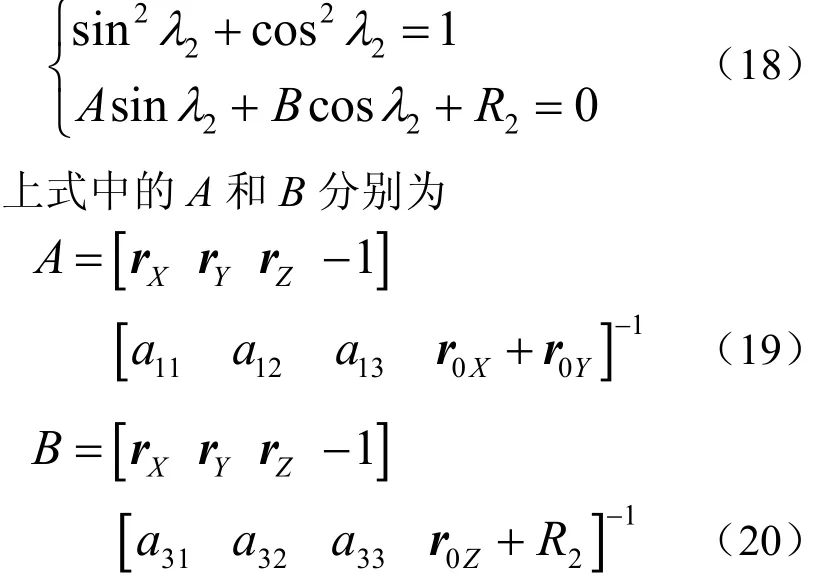
通过对方程组(18)求解,可得出倾角λ2
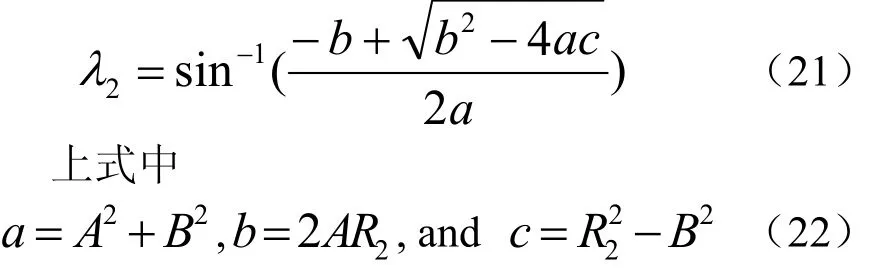
由以上分析可知,当在切触点处的邻近区域发生干涉时,可将初始的倾角λ1增大为λ2。而由公式(3)可知,当刀具半径R1和R2为一定值时,刀具曲面的最小法曲率随着倾角λ的增大而增大,因此当刀具倾角增大为λ2时,在切触点处刀具与加工曲面依然不会发生干涉。切触点邻近区域干涉判断与处理的算法流程图见图5所示。
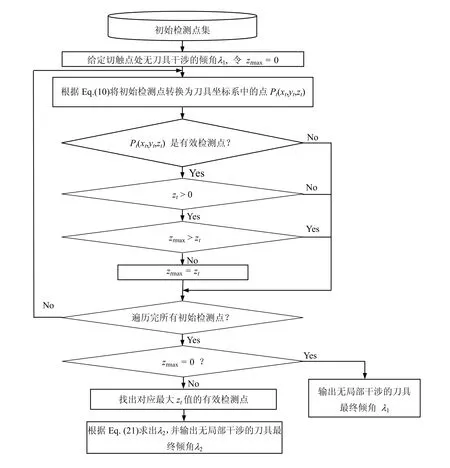
图5 切触点邻近区域的干涉判断与处理算法流程
3 实例计算及分析
本文以VC++及OpenGL为开发工具,针对NURBS(Non-uniform Rational B-spline,非均匀的有理B样条)曲面的数控加工,采用基于等参数法的刀具轨迹生成方法对上述干涉算法进行了验证,其刀具轨迹如图6所示。为了提高计算效率,利用NURBS曲面的二次泰勒展开式来计算曲面的第1类基本量E、F、G和第2类基本量L、M、N。以一个给定的加工误差δ=0.01mm,对加工轨迹曲线进行点的离散,通过计算各离散点处的最大法曲率,确定出加工曲面凹面上的最大法曲率Kmax=0.063,根据该最大法曲率初步选定刀具半径值R1=6mm,R2=5mm,然后给定一个刀具倾角λ0=30o、R2min=2mm,以及刀具半径的变化量∆R1=0.2mm和∆R2=0.2mm,通过迭代求解,得出环形铣刀最终的R1=6mm,R2=3.8mm。
为了验证以λ0=30o作为刀具半径选取依据是否合理,本文还分别对不同的λ0值,计算出其对应的刀具半径值,其计算结果如表1所示。从该表中可以明显看到,随着λ0值的增大,刀具的半径值也随着增大,虽然大的刀具半径能够提高切削效率,但是考虑到切触点邻近区域的干涉,最终的刀具倾角λ值可能会更大,这样不但会造成倾角超出机床允许的角度范围,而且还有可能使得刀具与加工曲面发生碰撞现象(全局干涉)。同样,若是λ值取得过小,则刀具尺寸也相应减小,过小的刀具尺寸不但影响加工效率,而且也影响刀具的切削强度,因此,经过以上综合分析,可以看出本文选取的λ0值是比较合理的。

图6 曲面加工刀具轨迹

表1 不同刀具倾角所对应的刀具半径值
4 结 论
本文针对光滑的具有C2连续的复杂曲面环形刀五轴数控加中的局部干涉问题,提出了一种基于曲率匹配及网格点的干涉检测方法。采用曲率匹配法能充分保证在切触点处沿各个方向上刀具曲面和被加工曲面不会发生过切现象,而采用网格点能够快速建立检测区域和检测点,因此,与传统干涉处理算法相比,本文的局部干涉处理算法具有更高的效率和可靠性。由于五轴加工相比于三轴加工具有更多地优越性,因此,在复杂曲面加工领域五轴加工占有越来越重要的地位。本文针对五轴加工中有关刀具干涉问题的研究,将为实现我国未来高精度、高速度的数字化制造奠定了基础,因此,具有很重要的现实和应用意义。
[1]Hosseinkhani Y, Akbari J, Vafaeesefat A. Penetrationelimination method for five-axis CNC machining of sculptured surfaces [J]. International Journal of Machine Tools & Manufacture, 2007, 47: 1625-1635.
[2]Jensen C G, Red W E, Pi J. Tool selection for five-axis curvature matched machining [J]. Computer-Aided Design, 2002, 34: 251-266.
[3]钟建琳, 米思南, 喻道远, 等. 曲面平头刀加工无干涉刀位轨迹自动生成的算法研究[J]. 机械工程学报,1999, 35(6): 93- 97.
[4]陈文亮, 曾建江, 李卫国, 等.复杂曲面刀具轨迹干涉的消除算法[J]. 东南大学学报(自然科学版), 2000,30(6): 44-47.
[5]Ahmet Can, Ali Unuvar. A novel iso-scallop tool-path generation for efficient five-axis machining of free-form surfaces [J]. International Journal of Advanced Manufacturing Technology, 2010, 51:1083-1098.
[6]Jensen CG, Anderson DC. Accurate tool placement and orientation for finish surface machining[C]//Proceedings of the Symposium on Concurrent Engineering, American Society of Mechanical Engineers, 1993: 127-145.
[7]Stanislav S, Makhanov. Adaptable geometric patterns for five-axis machining: a survey [J]. International Journal of Advanced Manufacturing Technology, 2010,47: 1167-1208.
[8]Cha-Soo S, Kyungduck C, Yuan-Shin L. Optimizing tool orientation for 5-axis machining by configuration-space search method [J]. Computer-Aided Design, 2003, 35: 549-566.
[9]Rao A, Sarma R. On local gouging in five-axis sculptured surface machining using flat-end tools [J].Computer- Aided Design, 2000, 32: 409-420.
[10]Javad M, Fard B, Feng H Y. Effect of tool tilt angle on machining strip width in five-axis flat-end milling of free-form surfaces [J]. International Journal of Advanced Manufacturing Technology, 2009, 44:211-222.
[11]程良骥, 伟 永, 章陈俊. 环形刀五轴数控加工刀具路径生成算法[J]. 机械工程学报, 2008, 44(3):205-212.
[12]Lee Y S. Admissible tool orientation control of gouging avoidance for 5-axis complex surface machining [J]. Computer-Aided Design, 1997, 29(7):507-521.
[13]Lin T, Lee J W, Erik L J B. A new accurate curvature matching and optimal tool based five-axis machining algorithm [J]. Journal of Mechanical Science and Technology, 2009, 23: 2624-2634.
[14]吴宝海, 罗 明, 张 莹, 等. 自由曲面五轴加工刀具轨迹规划技术的研究进展[J]. 机械工程学报,2008, 44(10): 9-18.
[15]李瑰贤. 空间几何建模及工程应用[M]. 北京: 高等教育出版社, 2007: 83-106.
[16]张 莹, 张定华, 吴宝海, 等. 复杂曲面环形刀五轴加工的自适应刀轴矢量优化方法[J]. 中国机械工程, 2008, 19(8): 945- 948.
[17]Li H, Feng HY. Efficient five-axis machining of free-form surfaces with constant scallop height tool paths [J]. International Journal of Production Research, 2004, 42: 2403-2417.
[18]Chiou CJ, Lee YS. Optimal tool orientation for five-axis tool-end machining by swept envelope approach [J]. Journal of Manufacturing Science and Engineering, 2005, 127: 810-818.
[19]Anotaipaiboon W, Makhanov S S. Tool path generation for five-axis NC machining using adaptive space-filling curves [J]. International Journal of Production Research, 2005, 43: 1643-1665.
